Битовые операции: что это, как работают и как применять на практике
Битовые операции — это манипуляции с данными на уровне отдельных битов, то есть самых элементарных единиц информации в компьютере. В отличие от привычных арифметических действий, которые работают с числами как с целостными величинами, побитовые операторы обрабатывают каждый бит независимо. Такой подход может показаться архаичным в эпоху высокоуровневых языков программирования, однако именно здесь кроется ключ к пониманию того, как на самом деле работает компьютер.

Основа битовых операций — булева алгебра, названная в честь математика Джорджа Буля. Эта формальная система оперирует только двумя значениями: истиной и ложью, или, в компьютерной интерпретации, единицей и нулём. На этих простых принципах построены все цифровые схемы — от простейших логических вентилей до современных процессоров.
- Базовые понятия: двоичная система, биты и таблицы истинности
- Основные битовые операции (подробное объяснение + примеры)
- Практические применения битовых операций в программировании
- Частые ошибки и подводные камни при работе с битовыми операциями
- Заключение
- Рекомендуем посмотреть курсы по разработке на языке C/C++
Базовые понятия: двоичная система, биты и таблицы истинности
Прежде чем погружаться в специфику операций, необходимо разобраться с фундаментальными понятиями. Бит (от англ. binary digit) — это минимальная единица информации, которая может принимать одно из двух значений: 0 или 1. Восемь битов составляют байт — стандартную единицу измерения объёма данных. Именно на этом уровне компьютер хранит и обрабатывает всю информацию: числа, текст, изображения, исполняемый код.
В двоичной системе счисления каждая позиция (разряд) представляет степень двойки. Например, число 53 в десятичной системе записывается как 110101 в двоичной: 1×2⁵ + 1×2⁴ + 0×2³ + 1×2² + 0×2¹ + 1×2⁰ = 32 + 16 + 4 + 1 = 53. Такое представление может показаться громоздким, но для компьютера оно естественно — процессор оперирует именно битами.
Таблицы истинности описывают поведение битовых операций для всех возможных комбинаций входных значений. Для бинарных операций (требующих двух операндов) они выглядят следующим образом:
- AND (И): результат равен 1, только если оба бита равны 1.
- OR (ИЛИ): результат равен 1, если хотя бы один бит равен 1.
- XOR (исключающее ИЛИ): результат равен 1, если биты различны.
- NOT (НЕ): унарная операция, инвертирующая значение бита.
В примерах мы часто будем использовать числа вместо отдельных символов, хотя операции применимы и к текстовым данным. Каждый символ в кодировке ASCII представлен числом от 0 до 127, а в Unicode — ещё большим диапазоном значений. Это означает, что битовые операции с символами — это, по сути, операции с их числовыми кодами.
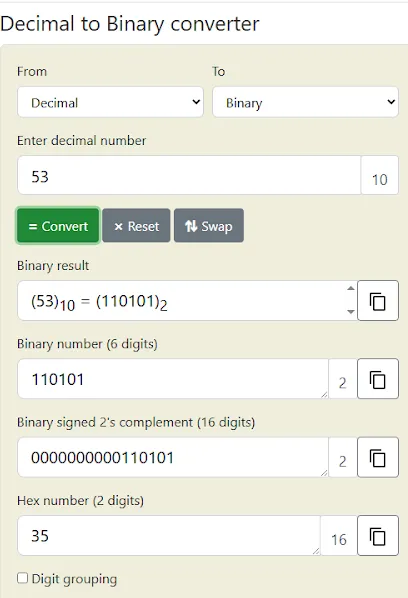
Онлайн-конвертер десятичного числа в двоичное с разложением по степеням двойки. Скриншот показывает реальный инструмент, который переводит число в двоичную систему. Это помогает читателю увидеть, что 53 → 110101 — не абстракция из учебника, а практический и проверяемый процесс.
Основные битовые операции (подробное объяснение + примеры)
Теперь, когда мы разобрались с теоретическим фундаментом, переходим к детальному рассмотрению каждой операции. Понимание их принципов работы — это не просто академическое упражнение, а практический навык, который пригодится при оптимизации кода, работе с аппаратными интерфейсами и решении нестандартных задач.
AND (&) — логическое И
Побитовое И — это операция, которая возвращает 1 в определённом разряде результата только тогда, когда соответствующие биты обоих операндов равны 1. Можно представить это как умножение битов: 1×1 = 1, все остальные комбинации дают 0.
Таблица истинности для AND:
| Бит A | Бит B | A & B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Рассмотрим практический пример с числами 38 и 53:
38 = 0010 0110 53 = 0011 0101 ────────────── & 36 = 0010 0100
Каждый разряд результата получен путём применения операции И к соответствующим битам операндов. Там, где оба бита равны 1 (второй и пятый разряды справа), в результате также получаем 1.
Практическое применение:
Одно из самых распространённых использований AND — работа с битовыми масками. Маска позволяет выделить или обнулить определённые биты числа. Например, чтобы проверить, является ли число чётным, достаточно выполнить операцию x & 1. Если младший бит равен 0 (результат операции равен 0), число чётное; если 1 — нечётное. Этот метод работает значительно быстрее, чем использование операции остатка от деления x % 2.
AND также используется для проверки установленных флагов в системном программировании. Например, если у вас есть набор флагов, упакованных в одно число, вы можете проверить конкретный флаг, применив маску с единицей в нужной позиции.
Типичная ошибка новичков: путать & с логическим оператором &&. Второй возвращает булево значение (true/false) и использует короткую оценку (не вычисляет второй операнд, если первый уже определяет результат), тогда как & работает с каждым битом независимо.
OR (|) — логическое ИЛИ
Побитовое ИЛИ работает по принципу объединения: результирующий бит равен 1, если хотя бы один из соответствующих битов операндов равен 1. Только когда оба бита равны 0, результат также будет 0.
Таблица истинности для OR:
| Бит A | Бит B | A | B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Посмотрим на пример с теми же числами 38 и 53:
38 = 0010 0110 53 = 0011 0101 ────────────── | 55 = 0011 0111
Обратите внимание: в результате единицы появляются во всех позициях, где хотя бы один из операндов имел 1. Это принципиальное отличие от AND, где требуется совпадение обоих битов.
Практическое применение:
Основная область использования OR — установка (включение) определённых битов без изменения остальных. Представьте, что у вас есть переменная, хранящая набор флагов-разрешений (чтение, запись, выполнение), и вам нужно добавить право на запись, не затрагивая остальные флаги. Операция permissions | WRITE_FLAG решает эту задачу элегантно и эффективно.
В графическом программировании OR используется для смешивания цветовых каналов или комбинирования различных режимов отображения. При работе с битовыми масками эта операция позволяет объединять несколько масок в одну.
Сравнение OR и AND:
Наглядная разница между этими операциями становится очевидной, если рассмотреть их как фильтры: AND оставляет только то, что есть в обоих операндах (пересечение), а OR собирает всё, что есть хотя бы в одном из них (объединение). В теории множеств это соответствует операциям пересечения и объединения.
XOR (^) — исключающее ИЛИ
Исключающее ИЛИ — пожалуй, самая интересная и неочевидная из битовых операций. Результирующий бит равен 1 только тогда, когда биты операндов различны. Если биты совпадают (оба 0 или оба 1), результат будет 0.
Таблица истинности для XOR:
| Бит A | Бит B | A ^ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Рассмотрим пример с числами 138 и 43:
138 в двоичном виде: 1000 1010
43 в двоичном виде: 0010 1011
Операция XOR (побитовое сложение по модулю 2):
1000 1010 ^ 0010 1011 1010 0001 ────────────
Перевод результата 1010 0001 в десятичную систему: 128+32+1=161.
Ключевое отличие XOR от обычного OR: когда оба бита равны 1, XOR возвращает 0, а не 1. Именно поэтому операция называется «исключающей» — она исключает случай одновременной истинности обоих операндов.
Практическое применение:
XOR обладает уникальным свойством обратимости: если A ^ B = C, то C ^ B = A и C ^ A = B. Это делает операцию незаменимой в некоторых алгоритмах.
Обмен переменных без дополнительной памяти:
Классический трюк с XOR позволяет поменять значения двух переменных без использования временной:
a = a ^ b; b = a ^ b; // теперь b = a (исходное) a = a ^ b; // теперь a = b (исходное)
Хотя этот метод редко используется в production-коде (современные компиляторы оптимизируют обычный обмен через временную переменную не хуже), он демонстрирует элегантность битовых операций.
Простейшее шифрование:
XOR лежит в основе некоторых криптографических алгоритмов. Простейший вариант — XOR каждого символа сообщения с символом-ключом:
String msg = "Secret message";
char[] message = msg.toCharArray();
char key = 'K';
String encrypted = "";
for(int i = 0; i < message.length; i++){
encrypted += (char)(message[i] ^ key);
}
Для расшифровки достаточно повторить ту же операцию — благодаря обратимости XOR. Более сложный вариант использует строку-ключ с циклическим повторением символов. Конечно, такое шифрование легко взламывается, но XOR остаётся важным элементом серьёзных криптографических систем.
Показывает, что символ = число = биты. Это усиливает мысль о том, что побитовые операции применимы и к тексту.
NOT (~) — логическое НЕ (инверсия битов)
Побитовое отрицание — унарная операция, то есть применяется к одному операнду. Она инвертирует все биты числа: каждый 0 становится 1, а каждая 1 превращается в 0. На первый взгляд всё просто, но именно здесь начинающие разработчики сталкиваются с неожиданными результатами.
Таблица истинности для NOT:
| Бит A | ~A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Рассмотрим пример с числом 52:
52 = 0011 0100 ───────────── ~52 = 1100 1011
Казалось бы, инвертировав биты числа 52 (которое в 8-битном представлении равно 00110100), мы должны получить 11001011, то есть 203 в десятичной системе. Однако если вы выполните эту операцию в реальной программе, результатом будет -53. Почему?
Дополнительный код и представление отрицательных чисел:
Здесь вступает в силу концепция дополнительного кода (two’s complement) — стандартный способ представления отрицательных целых чисел в компьютерах. В этой системе старший (самый левый) бит является знаковым: если он равен 0, число положительное; если 1 — отрицательное.
Для получения отрицательного числа в дополнительном коде необходимо:
- Инвертировать все биты исходного числа (применить NOT).
- Добавить к результату 1.
Например, для числа 109:
109 = 0110 1101 ~109 = 1001 0010 (инверсия) +1 = 1001 0011 (это -109 в дополнительном коде)
Именно поэтому операция ~x всегда даёт результат -(x + 1). Это не ошибка или странность языка программирования — это фундаментальное свойство работы с числами в современных процессорах.
Практическое применение:
NOT используется для инверсии битовых масок. Если у вас есть та, которая находит определённые биты, ~mask даст обратную маску. Это полезно при сбросе флагов: value & ~flag обнулит биты, установленные в flag, не затрагивая остальные.
В графическом программировании инверсия битов применяется для работы с цветами — например, для получения негатива изображения или инвертирования отдельных цветовых каналов.
Побитовые сдвиги (<<, >>, >>>)
Операции сдвига перемещают все биты числа влево или вправо на указанное количество позиций. В отличие от рассмотренных ранее операций, сдвиги не сравнивают биты двух операндов, а манипулируют разрядами одного числа. При этом они обладают интересным побочным эффектом — выполняют умножение или деление на степени двойки.
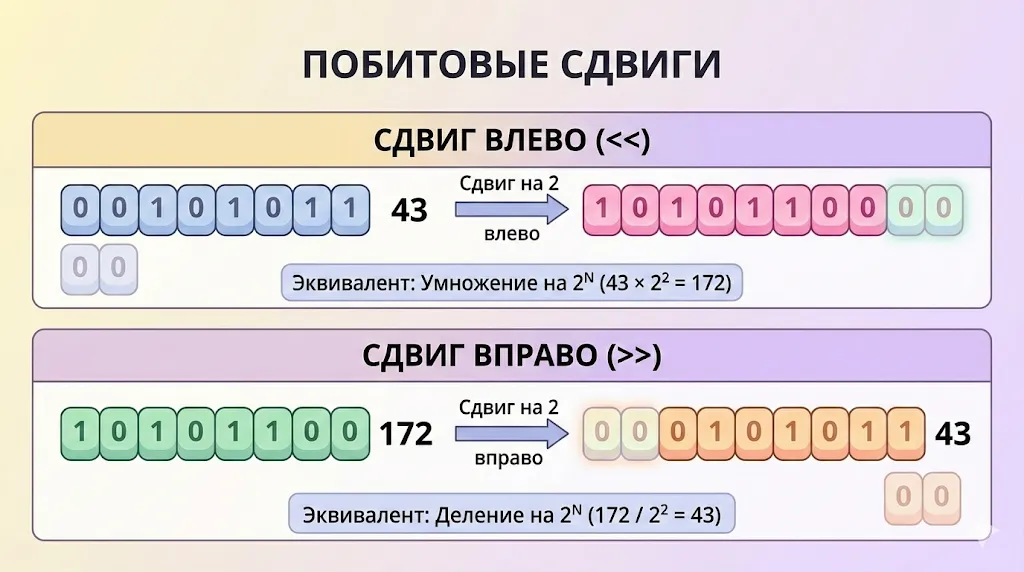
Иллюстрация работы побитовых сдвигов. Сдвиг влево (<<) перемещает биты налево и эквивалентен умножению на степень двойки. Сдвиг вправо (>>) перемещает биты направо и эквивалентен целочисленному делению на степень двойки. Обратите внимание, как освободившиеся разряды заполняются нулями.
Побитовый сдвиг влево (<<):
Сдвиг влево перемещает все биты числа на N позиций влево, а освободившиеся младшие разряды заполняются нулями. Биты, выходящие за границу разрядной сетки слева, теряются.
43 = 0010 1011 43<<2 = 1010 1100 = 172
Математически сдвиг влево на N позиций эквивалентен умножению числа на 2ᴺ. То есть 43 << 2 равносильно 43 × 2² = 43 × 4 = 172. Это свойство делает сдвиги невероятно эффективным инструментом оптимизации: процессору гораздо проще сдвинуть биты, чем выполнить полноценное умножение.
Побитовый сдвиг вправо (>>):
Сдвиг вправо перемещает биты на N позиций вправо. Поведение этой операции зависит от знака числа. Для положительных чисел освободившиеся старшие разряды заполняются нулями, для отрицательных — единицами. Такой подход называется арифметическим сдвигом и сохраняет знак числа в соответствии с дополнительным кодом.
172 = 1010 1100 172>>2 = 0010 1011 = 43
Сдвиг вправо на N позиций эквивалентен делению на 2ᴺ с округлением вниз. Таким образом, 172 >> 2 даёт 172 / 4 = 43.
Логический сдвиг вправо (>>>):
В некоторых языках (например, Java) существует третий оператор сдвига — логический сдвиг вправо. В отличие от арифметического >>, операция >>> всегда заполняет старшие разряды нулями, независимо от знака числа. Это полезно при работе с беззнаковыми числами или когда нужно интерпретировать число как последовательность битов без учёта знака.
Таблица операций сдвига:
| Операция | Направление | Заполнение освобождённых битов | Эквивалент |
|---|---|---|---|
| << | Влево | Нулями | Умножение на 2ᴺ |
| >> | Вправо | По знаку (0 или 1) | Деление на 2ᴺ |
| >>> | Вправо | Всегда нулями | Логическое деление |
Практическое применение: сдвиги широко используются для оптимизации арифметических операций. Выражение x << 3 выполняется значительно быстрее, чем x * 8, хотя результат идентичен. Современные компиляторы часто выполняют такую оптимизацию автоматически, но в критичных к производительности участках кода явное использование сдвигов остаётся актуальным.
Другое применение — упаковка и распаковка данных. Например, если нужно объединить четыре байта в одно 32-битное число, можно использовать комбинацию сдвигов и OR:
int packed = (byte1 << 24) | (byte2 << 16) | (byte3 << 8) | byte4;
Обратная операция — извлечение отдельных байтов — выполняется сочетанием сдвига вправо и маскирования через AND.
Практические применения битовых операций в программировании
Теория битовых операций становится по-настоящему ценной, когда мы переходим к практическим задачам. Несмотря на кажущуюся архаичность работы с битами, эти техники остаются актуальными в современной разработке — от системного программирования до оптимизации высоконагруженных приложений.
Битовые маски: установка, сброс и проверка флага
Битовые маски — один из самых элегантных способов работы с наборами флагов или опций. Вместо создания множества булевых переменных мы можем упаковать до 32 (или 64) флагов в одно целое число, где каждый бит представляет отдельное состояние.
Установка флага выполняется через OR:
int permissions = 0b0000; // изначально нет прав permissions |= 0b0100; // добавляем право на запись // permissions теперь равен 0b0100
Сброс флага требует комбинации NOT и AND:
permissions &= ~0b0100; // убираем право на запись // permissions снова равен 0b0000
Проверка флага использует AND:
if ((permissions & 0b0100) != 0) {
// право на запись установлено
}
Такой подход активно применяется в системном программировании (права доступа к файлам в UNIX), графических API (флаги режимов отрисовки в OpenGL), сетевых протоколах (флаги в заголовках TCP/IP) и многих других областях, где важна компактность представления данных.
Быстрая проверка свойств числа
Битовые операции позволяют проверять некоторые математические свойства чисел гораздо эффективнее традиционных методов.
Проверка чётности:
boolean isEven = (x & 1) == 0;
Эта операция работает потому, что в двоичном представлении младший бит нечётных чисел всегда равен 1, а чётных — 0. На некоторых архитектурах & 1 выполняется на 60-70% быстрее, чем % 2.
Проверка степени двойки:
boolean isPowerOfTwo = (x > 0) && ((x & (x - 1)) == 0);
Этот изящный трюк основан на том, что числа-степени двойки в двоичной форме содержат ровно одну единицу (4 = 0100, 8 = 1000, 16 = 10000). Вычитание единицы инвертирует все биты после этой единицы, и операция AND с исходным числом даёт ноль.
Простейшее шифрование XOR
Как мы уже упоминали, XOR обладает свойством обратимости, что делает его основой для шифрования. Базовый алгоритм выглядит так:
String encrypt(String text, String key) {
StringBuilder result = new StringBuilder();
for (int i = 0; i < text.length(); i++) {
result.append((char)(text.charAt(i) ^ key.charAt(i % key.length())));
}
return result.toString();
}
Расшифровка выполняется той же функцией — применяем XOR с тем же ключом повторно, и получаем исходный текст. Разумеется, такой метод не обеспечивает криптографическую стойкость и легко взламывается частотным анализом, но XOR остаётся важным компонентом серьёзных шифров (например, в алгоритме AES).
Использование сдвигов для оптимизации
Сдвиги предоставляют быстрый способ выполнения умножения и деления на степени двойки, а также решения задач упаковки данных.
Быстрое умножение и деление:
int multiplyBy8 = x << 3; // быстрее чем x * 8 int divideBy4 = x >> 2; // быстрее чем x / 4
Упаковка RGB-цвета в одно число:
int color = (red << 16) | (green << 8) | blue;
Извлечение компонентов обратно:
int red = (color >> 16) & 0xFF; int green = (color >> 8) & 0xFF; int blue = color & 0xFF;
Такая техника широко используется в графическом программировании, где цвет часто представлен одним 32-битным числом, упаковывающим значения красного, зелёного, синего каналов и прозрачности.

Практический пример использования битовых сдвигов и операции OR для упаковки компонентов цвета (Красный, Зеленый, Синий) в одно 32-битное целое число. Сдвиги на 16 и 8 позиций позволяют разместить значения каждого канала в отведенном ему 8-битном сегменте.
Частые ошибки и подводные камни при работе с битовыми операциями
Битовые операции, при всей своей элегантности, таят в себе ловушки, в которые регулярно попадают как начинающие, так и опытные разработчики. Понимание этих подводных камней поможет избежать трудноуловимых багов и неожиданного поведения программы.
- Путаница между битовыми и логическими операторами. Самая распространённая ошибка — использование & вместо && или | вместо || в условных выражениях. Код if (x > 0 & y < 10) технически корректен, но работает не так, как задумано: оба условия всегда вычисляются, даже если первое ложно, а результат будет зависеть от побитовой операции над булевыми значениями. Логический оператор && использует короткую оценку и более очевиден в намерениях. Обратная ошибка — применение && там, где нужна побитовая операция — приведёт к совершенно иным результатам.
- Неожиданные результаты оператора NOT. Новички часто ожидают, что ~5 даст что-то вроде инвертированных битов числа 5 в пределах одного байта. На практике из-за дополнительного кода ~5 равно -6. Это может сбивать с толку, особенно при работе с масками. Формула ~x = -(x + 1) работает всегда, но её необходимо держать в уме.
- Переполнение при больших сдвигах. Сдвиг на количество позиций, превышающее размер типа данных, даёт undefined behavior или неожиданные результаты. В Java сдвиг на n позиций фактически выполняется на n % 32 для int и n % 64 для long. То есть x << 33 для int-переменной эквивалентно x << 1, что редко является желаемым поведением.
- Приоритет операторов. Битовые операторы имеют более низкий приоритет, чем арифметические, но более высокий, чем операторы сравнения. Выражение x & 0xFF == 0 интерпретируется как x & (0xFF == 0), а не (x & 0xFF) == 0. Скобки здесь не опциональны — они обязательны для корректной работы кода.
- Проблемы со сдвигами отрицательных чисел. Арифметический сдвиг вправо (>>) сохраняет знак числа, заполняя старшие разряды единицами для отрицательных чисел. Это может привести к неожиданностям:
int x = -8; // 11111111111111111111111111111000 int y = x >> 2; // 11111111111111111111111111111110 = -2
Если вам нужен логический сдвиг (без сохранения знака), используйте >>>. Разница критична при работе с битовыми полями или при интерпретации чисел как беззнаковых значений.
Заключение
Мы рассмотрели весь спектр битовых операций — от базовых принципов до практических применений. Теперь давайте систематизируем полученные знания в виде простых мнемонических правил, которые помогут быстро вспомнить суть каждой операции:
- Битовые операции работают на уровне отдельных битов. Это позволяет управлять данными максимально точно и эффективно.
- Основные операторы AND, OR, XOR и NOT основаны на булевой алгебре. Их понимание помогает лучше разобраться в логике работы компьютера.
- Побитовые сдвиги позволяют быстро умножать и делить числа на степени двойки. Это используется для оптимизации вычислений и работы с данными.
- Битовые маски дают возможность хранить множество флагов в одном числе. Такой подход экономит память и упрощает управление состояниями.
- Операция XOR применяется не только в логике, но и в простейших алгоритмах шифрования. Её обратимость делает её полезной в ряде практических задач.
- Работа с дополнительным кодом объясняет, почему побитовое отрицание даёт отрицательные числа. Это важно учитывать при использовании оператора NOT.
- Битовые операции широко применяются в системном программировании, графике и сетевых протоколах. Они остаются актуальными даже в современных языках высокого уровня.
Если вы только начинаете осваивать профессию программиста, рекомендуем обратить внимание на подборку курсов по разработке на C и C++. В них есть теоретическая и практическая часть, которые помогают лучше понять, как применять битовые операции и другие фундаментальные инструменты на практике.
Рекомендуем посмотреть курсы по разработке на языке C/C++
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Разработчик на C++
|
Skillbox
218 отзывов
|
Цена
Ещё -20% по промокоду
138 734 ₽
277 467 ₽
|
От
4 080 ₽/мес
Это минимальный ежемесячный платеж за курс.
|
Длительность
12 месяцев
|
Старт
3 февраля
|
Подробнее |
|
C++ разработчик игр
|
XYZ School
21 отзыв
|
Цена
Ещё -14% по промокоду
90 300 ₽
129 000 ₽
|
От
6 500 ₽/мес
|
Длительность
4 месяца
|
Старт
5 февраля
|
Подробнее |
|
C++. Практикум. Часть 1
|
Stepik
33 отзыва
|
Цена
850 ₽
|
|
Длительность
1 день
|
Старт
31 января
|
Подробнее |

Что выбрать: ITSM или ITIL? Ответ для бизнеса
ITSM и ITIL часто упоминаются вместе, но что это такое на самом деле? Узнайте, как эти концепции помогают улучшить IT-услуги и оптимизировать процессы

Что такое псевдокод простыми словами
Что такое псевдокод и почему его используют даже опытные разработчики? В статье разбираем, как он помогает проектировать алгоритмы, готовиться к собеседованиям и упрощать командную работу.

Тестовые задания для дизайнеров: работать бесплатно или шанс на успех?
Тестовое задание для дизайнера — возможность показать свои навыки, но не всегда оно того стоит. Как отличить полезное задание от неоправданной траты времени?

Как контейнеризировать приложение в Docker: пошаговая инструкция от подготовки кода до деплоя
Как упаковать приложение в docker так, чтобы оно стабильно работало в любом окружении — от локальной машины до продакшена? В статье разбираем контейнеризацию шаг за шагом и показываем, как избежать типичных ошибок при сборке и деплое.