Фракталы, которые правят миром: как математика проникает в хаос
В мире математики и визуального искусства существуют объекты настолько завораживающие своей красотой, что на них можно смотреть бесконечно долго. Фракталы — именно такое явление, представляющее собой математические структуры с уникальным свойством самоподобия.

В самом простом определении, фрактал — это геометрическая фигура, в которой один и тот же паттерн повторяется в разных масштабах. Проще говоря, если мы увеличим любую часть фрактала, то увидим структуру, похожую на исходную фигуру целиком. При этом количество повторяющихся частей у настоящего фрактала стремится к бесконечности, что отличает его от обычных самоподобных геометрических фигур с конечным числом звеньев (называемых предфракталами).
В отличие от классических евклидовых фигур (прямых линий, треугольников, квадратов), которые мы привыкли видеть в учебниках геометрии, фракталы позволяют описывать сложные природные объекты — от ветвей деревьев до береговых линий и облаков. В природе практически не существует идеальных геометрических форм, и фрактальная геометрия предлагает математический аппарат для моделирования этой естественной сложности.
Фракталы находятся на удивительном перекрестке между строгой математикой, компьютерными технологиями, природой и искусством. Они дают нам возможность не только анализировать сложные структуры, но и создавать визуально потрясающие изображения, основанные на простых математических правилах.
- История и происхождение фракталов
- Что делает фрактал фракталом? Основные свойства
- Виды фракталов
- Геометрические фракталы
- Алгебраические фракталы
- Стохастические фракталы
- Примеры фракталов в реальной жизни
- Применение фракталов в науке и технике
- Компьютерная графика и визуализация данных
- Моделирование природных процессов
- Заключение: Почему фракталы важны?
История и происхождение фракталов
Термин «фрактал» впервые был введен в научный обиход в 1975 году американским математиком Бенуа Мандельбротом, который взял за основу латинское слово fractus, означающее «разделённый на части» или «дробленый». Однако интересно, что сами по себе фрактальные структуры были известны математикам задолго до формального определения этого понятия.
Первая математическая фигура, которую мы сегодня классифицируем как фрактал, была открыта немецким математиком Георгом Кантором ещё в 1883 году. Созданное им «множество Кантора» демонстрировало как самоподобие, так и рекурсию — два ключевых свойства, которые впоследствии станут определяющими для фракталов. Позже, в начале XX века, шведский математик Хельге фон Кох создал свою знаменитую «снежинку», а польский математик Вацлав Серпинский описал треугольник, носящий теперь его имя.
Настоящий прорыв произошел в 1970-х, когда Мандельброт не только систематизировал существующие знания, но и существенно расширил теорию фракталов. В 1982 году он опубликовал свою знаменитую книгу «Фрактальная геометрия природы» (The Fractal Geometry of Nature), которая представила новый метод описания сложных природных объектов на основе фрактальных структур.
Появление компьютеров сыграло решающую роль в развитии фрактальной геометрии. Впервые стало возможным визуализировать сложные математические формулы и увидеть удивительную красоту, скрытую в рекурсивных алгоритмах. Множество Мандельброта, визуализированное с помощью компьютера в 1980 году, стало одной из самых узнаваемых математических структур в мире и символом союза между математикой и компьютерными технологиями.
Что делает фрактал фракталом? Основные свойства
Чтобы структура могла считаться настоящим фракталом, она должна обладать рядом специфических свойств, которые отличают её от обычных геометрических форм. Давайте разберемся, какие основные характеристики делают фрактал фракталом.
Основополагающим свойством является самоподобие — феномен, при котором части объекта в той или иной степени повторяют структуру целого. Проще говоря, если мы увеличим фрагмент фрактала, мы обнаружим структуру, напоминающую исходную фигуру. При этом самоподобие может быть как точным (как в треугольнике Серпинского), так и приближенным (как у фрактальных облаков или береговых линий).
Вторым ключевым свойством является рекурсивность — повторение одного и того же набора правил на каждом этапе построения. В отличие от классической геометрии, где фигуры описываются конечным набором параметров, фрактал теоретически можно строить бесконечно, углубляясь во всё более мелкие детали.
Важной математической характеристикой фракталов выступает дробная размерность. В то время как точка имеет размерность 0, линия — 1, а плоскость — 2, фракталы часто имеют дробную размерность. Например, размерность кривой Коха составляет примерно 1,2618, что математически объясняет её положение между линией и плоскостью.
| Свойство | Описание | Пример |
|---|---|---|
| Самоподобие | Части объекта похожи на целое | Веточки дерева повторяют структуру всего дерева |
| Рекурсивность | Повторение одних и тех же правил на разных масштабах | Каждая итерация строительства снежинки Коха |
| Дробная размерность | Размерность, занимающая промежуточное положение между целыми числами | Множество Кантора имеет размерность приблизительно 0,631 |
| Бесконечная детализация | Возможность бесконечного увеличения с обнаружением новых деталей | Множество Мандельброта при увеличении показывает новые структуры |
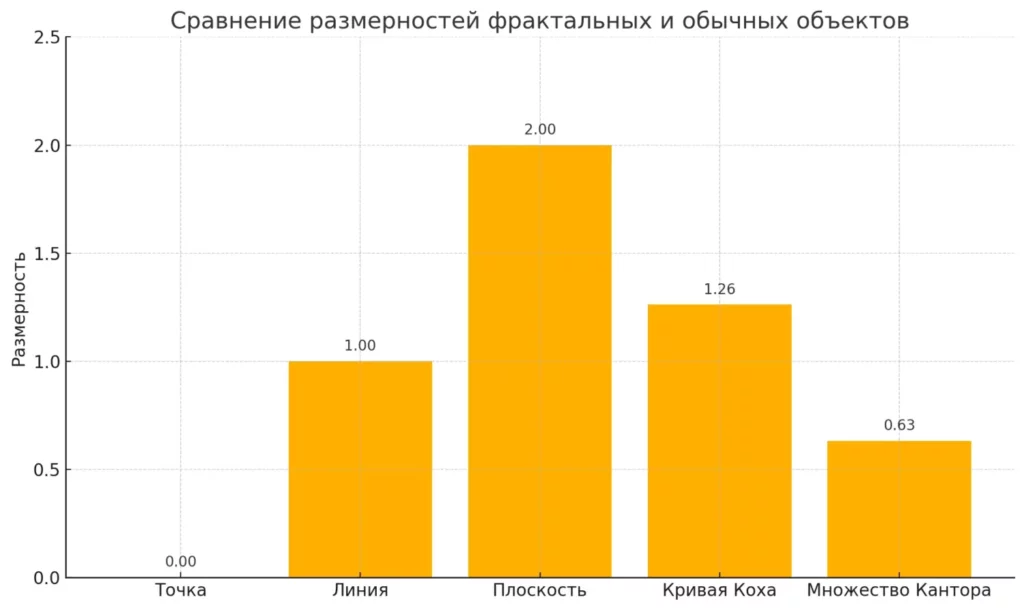
Визуализация, иллюстрирующая, как фракталы отличаются от классических геометрических объектов благодаря своей дробной размерности
Именно сочетание этих свойств делает фракталы уникальным математическим и природным явлением, позволяющим описывать сложные структуры относительно простыми формулами и алгоритмами.
Виды фракталов
В мире фрактальной геометрии существует впечатляющее разнообразие форм и структур, которые исследователи классифицируют по различным принципам. В современной науке принято выделять три основных класса фракталов, каждый из которых характеризуется своими методами построения и математическими свойствами.
Такое разделение на категории не просто теоретическое упражнение — оно имеет практическое значение, поскольку определяет методы работы с фракталами в различных прикладных областях от компьютерной графики до моделирования физических процессов. Каждый тип фракталов находит своё применение в зависимости от поставленных задач и желаемых результатов.
Геометрические фракталы строятся на основе простых геометрических фигур, которые определённым образом делятся и преобразуются на каждой итерации по строго заданным правилам. Такие фракталы, как правило, являются наиболее наглядными для понимания основных принципов фрактальной геометрии, поскольку процесс их построения можно легко визуализировать и проследить шаг за шагом.
Алгебраические фракталы представляют собой более сложную категорию, поскольку строятся на основе алгебраических формул и итерационных процессов в комплексной плоскости. В отличие от геометрических фракталов, их структура не так очевидна на первый взгляд, но они производят одни из самых завораживающих визуальных образов в математике.
Стохастические фракталы отличаются тем, что в их построении присутствует элемент случайности. В этих структурах на каждой итерации некоторые параметры изменяются случайным образом, что приводит к образованию фракталов, наиболее близко имитирующих природные объекты с их естественной вариативностью.
Каждый класс фракталов по-своему уникален и представляет интерес как для теоретической математики, так и для практических приложений. В следующих разделах мы рассмотрим каждый тип более подробно, исследуя его особенности и примеры.
Геометрические фракталы
Геометрические фракталы представляют собой наиболее интуитивно понятный класс фрактальных структур. Их построение начинается с базовой геометрической формы — отрезка, треугольника, квадрата или другой простой фигуры, которая затем модифицируется по определенным правилам с каждой новой итерацией. Ключевым аспектом в построении геометрических фракталов является точное следование заданному алгоритму, без каких-либо случайных отклонений.
Рассмотрим несколько классических примеров, которые наглядно демонстрируют принципы формирования геометрических фракталов:
- Множество Кантора — исторически первый фрактал, описанный немецким математиком Георгом Кантором в 1883 году. Процесс построения начинается с отрезка, который делится на три равные части, после чего средняя часть удаляется. Затем эта процедура рекурсивно применяется к оставшимся отрезкам. Несмотря на кажущуюся простоту, это множество обладает удивительными математическими свойствами.
- Кривая Коха (снежинка Коха) — фрактал, созданный шведским математиком Хельге фон Кохом в 1904 году. Построение начинается с отрезка, средняя треть которого заменяется двумя отрезками, образующими равносторонний треугольник (без основания). Этот процесс повторяется для каждого нового отрезка. В замкнутой форме этот фрактал напоминает снежинку с бесконечно детализированными краями.
- Треугольник Серпинского — еще один классический геометрический фрактал, предложенный польским математиком Вацлавом Серпинским. Строится путем деления равностороннего треугольника на четыре меньших, с последующим удалением центрального. Этот процесс затем повторяется для каждого из трёх оставшихся треугольников.
- Ковёр Серпинского — двумерный аналог треугольника Серпинского, в котором вместо треугольника используется квадрат, разделенный на девять меньших квадратов, с удалением центрального.
- Губка Менгера — трехмерное расширение ковра Серпинского, представляющее собой куб, разделенный на 27 меньших кубов, из которых удаляются центральный и шесть кубов, примыкающих к центру каждой грани.
Основные виды геометрических фракталов:
- Линейные фракталы (кривая Коха, кривая Пеано)
- Плоскостные фракталы (треугольник и ковёр Серпинского)
- Объемные фракталы (губка Менгера, пирамида Серпинского)
- Древовидные фракталы (дерево Пифагора, L-системы)
В отличие от других типов фракталов, геометрические фракталы всегда предсказуемы и детерминированы, что делает их особенно ценными для образовательных целей и иллюстрации основных принципов фрактальной геометрии.
Алгебраические фракталы
Алгебраические фракталы представляют собой, пожалуй, наиболее впечатляющий и математически сложный класс фрактальных структур. В отличие от геометрических фракталов, они строятся не путем преобразования базовых геометрических фигур, а на основе алгебраических формул, особенно тех, что включают итерационные процессы в комплексной плоскости.
Несмотря на свою математическую сложность, именно алгебраические фракталы приобрели наибольшую известность среди широкой публики благодаря их потрясающей визуальной эстетике. Наиболее известными представителями этого класса являются множество Мандельброта и множество Жюлиа.
Множество Мандельброта — настоящая икона фрактальной геометрии. Этот фрактал описывается элегантной математической формулой: Zₙ₊₁ = Zₙ² + C, где Z и C — комплексные числа. Точка комплексной плоскости принадлежит множеству Мандельброта, если при итерационном применении этой формулы последовательность Zₙ остается ограниченной. Примечательно, что, несмотря на простоту формулы, результирующая фигура обладает бесконечной сложностью и неисчерпаемым богатством деталей. Увеличивая любой участок границы этого множества, мы обнаруживаем новые миниатюрные копии всего множества вместе с уникальными структурами, которые нигде более не повторяются.
Множество Жюлиа — тесно связано с множеством Мандельброта и строится по похожей формуле. Однако в этом случае параметр C является константой для каждого конкретного множества Жюлиа, что дает бесконечное семейство различных фракталов — по одному для каждого значения C. Интересно, что между множествами Мандельброта и Жюлиа существует глубокая связь: форма множества Жюлиа для конкретного значения C зависит от того, находится ли точка C внутри или вне множества Мандельброта.
| Характеристика | Множество Мандельброта | Множество Жюлиа |
|---|---|---|
| Базовая формула | Zₙ₊₁ = Zₙ² + C (C — варьируется, Z₀ = 0) | Zₙ₊₁ = Zₙ² + C (C — фиксировано) |
| Визуальное представление | Единая связная структура | Может быть как связным, так и пылевидным |
| Количество фракталов | Единственное | Бесконечное семейство (для каждого C) |
| Связь с другими фракталами | Является «картой» множеств Жюлиа | Характер зависит от положения C относительно множества Мандельброта |
Алгебраические фракталы имеют особое значение не только для математики, но и для теории динамических систем, поскольку наглядно демонстрируют, как простые формулы при итерационном применении могут приводить к невероятно сложному и непредсказуемому поведению.
Стохастические фракталы
В отличие от строго детерминированных геометрических и алгебраических фракталов, стохастические (или случайные) фракталы вносят элемент непредсказуемости в процесс своего формирования. Именно этот класс фракталов наиболее тесно связан с моделированием природных явлений, поскольку в природе редко встречаются идеально правильные формы — всегда присутствует элемент случайности и вариативности.
Стохастические фракталы образуются в том случае, если в итерационной системе случайным образом изменяются один или несколько параметров. При этом ключевое свойство самоподобия сохраняется, но проявляется в статистическом смысле — части объекта похожи на целое не точно, а с определенной степенью вероятности. Эта особенность делает данный тип фракталов особенно ценным для компьютерного моделирования таких природных объектов, как горные ландшафты, облака, береговые линии или даже биологические структуры.
Один из простейших методов создания стохастических фракталов — это случайное смещение средней точки (midpoint displacement). Алгоритм начинается с прямой линии, затем её средняя точка смещается вверх или вниз на случайную величину. Этот процесс рекурсивно повторяется для каждого нового отрезка, создавая со временем реалистичный профиль горного хребта или береговой линии.
Более сложные алгоритмы, такие как метод броуновского движения частиц или система итерируемых функций с вероятностными параметрами (IFS — Iterated Function Systems), позволяют создавать двумерные и трехмерные стохастические фракталы, поразительно напоминающие облака, деревья или даже целые ландшафты.
Примечательно, что именно стохастические фракталы нашли наиболее широкое применение в компьютерной графике и кинематографе для создания реалистичных текстур и пейзажей. Это объясняется тем, что природные объекты редко демонстрируют точное самоподобие — чаще мы наблюдаем статистическое самоподобие с элементами случайности, что идеально описывается моделями стохастических фракталов.
Примеры фракталов в реальной жизни
Фрактальная геометрия не ограничивается абстрактными математическими моделями — она окружает нас повсюду в природе. Наблюдательному взгляду фрактальные структуры откроются практически в любом природном ландшафте или биологическом объекте. Удивительно, но именно фрактальный принцип построения оказывается наиболее эффективным и энергетически выгодным для многих природных систем.
Растительный мир предлагает одни из самых наглядных примеров фракталов. Деревья с их ветвящимися структурами, где каждая ветвь подобна миниатюрному дереву, служат классическим примером самоподобия. Папоротники демонстрируют еще более чёткую фрактальную структуру — каждый листок состоит из меньших листочков, которые в свою очередь повторяют структуру целого. Но, пожалуй, самым поразительным примером природного фрактала является капуста Романеско — разновидность цветной капусты, в которой каждый бутон представляет собой точную копию всего растения в миниатюре, образуя логарифмическую спираль с фрактальной структурой.
Системы циркуляции в живых организмах также часто имеют фрактальное строение. Кровеносная система, бронхиальное дерево легких, нейронные сети — все эти структуры многократно ветвятся, образуя самоподобные паттерны на разных масштабах. Такая организация позволяет максимально эффективно заполнять пространство и обеспечивать оптимальную доставку веществ ко всем тканям организма.
Географические объекты также демонстрируют фрактальные свойства. Береговые линии, горные хребты, системы рек и их притоков — все эти объекты обладают статистическим самоподобием. Знаменитый вопрос «Какова длина береговой линии Великобритании?», поставленный Мандельбротом, наглядно демонстрирует фрактальную природу побережий: чем более детальное измерение мы проводим, тем длиннее оказывается линия из-за бесконечной сложности естественных изгибов.
Атмосферные явления, такие как облака и снежинки, представляют собой еще одну область, где фрактальная геометрия находит своё проявление. Каждая снежинка, хотя и уникальна, строится по принципам фрактальной симметрии. Молнии, разветвляющиеся от основного канала, также следуют фрактальному паттерну, находя путь наименьшего сопротивления в атмосфере.
Удивительно, но даже космические структуры — от распределения звезд в галактиках до крупномасштабной структуры Вселенной — демонстрируют признаки фрактального самоподобия, что наводит некоторых космологов на мысль о том, что фрактальная геометрия может быть фундаментальным принципом организации материи во Вселенной.
Применение фракталов в науке и технике
Фрактальная геометрия преодолела путь от чисто математической концепции до инструмента, применяемого в самых разнообразных областях науки и техники. Универсальность фрактальных моделей объясняется их способностью эффективно описывать сложные, нерегулярные структуры, которые встречаются повсеместно как в природе, так и в созданных человеком системах.
В физике фракталы нашли применение для описания процессов диффузии, турбулентных потоков и фазовых переходов. Особенно интересно их использование в теории хаоса, где фрактальные аттракторы помогают визуализировать и понять динамику нелинейных систем. Концепция фрактальной размерности позволяет количественно характеризовать хаотические процессы, которые раньше казались непредсказуемыми и не поддающимися математическому описанию.
В радиоэлектронике фрактальные антенны произвели настоящую революцию. Созданные американским инженером Натаном Коэном в 1995 году, эти компактные устройства, имеющие форму, основанную на фрактальных паттернах (например, на кривой Коха), обладают широким диапазоном рабочих частот, занимая при этом намного меньше пространства, чем традиционные антенны. Это свойство оказалось особенно ценным для мобильных устройств, где компактность имеет решающее значение.
В медицине фрактальный анализ применяется для диагностики различных патологических состояний. Структура кровеносных сосудов, нейронных сетей, а также паттерны сердечного ритма могут быть проанализированы с помощью фрактальных методов, что позволяет выявить отклонения от нормы на ранних стадиях заболеваний. Некоторые исследователи даже используют фрактальную геометрию для понимания роста раковых опухолей и распространения эпидемий.
В экономике и финансах теория фракталов применяется для анализа временных рядов и прогнозирования движения рынков. Фрактальная гипотеза рынка, предложенная Бенуа Мандельбротом, представляет альтернативу классической гипотезе эффективного рынка и помогает объяснить такие явления, как кластеризация волатильности и «тяжелые хвосты» распределений цен активов.
Примечательно, что фрактальные методы также находят применение в таких разнообразных областях, как геология (для моделирования залежей полезных ископаемых), экология (для исследования биологического разнообразия), и даже в археологии (для анализа пространственного распределения артефактов). Эта универсальность подчеркивает фундаментальную роль фрактальной геометрии как языка для описания сложных систем, независимо от их конкретной природы.
Компьютерная графика и визуализация данных
Пожалуй, наиболее заметной и визуально впечатляющей областью применения фракталов стала компьютерная графика. Фрактальные алгоритмы произвели революцию в способах генерации реалистичных природных ландшафтов, текстур и визуальных эффектов, открыв новые горизонты для дизайнеров и аниматоров.
Ключевое преимущество фрактальной графики заключается в её компактности. В отличие от традиционных подходов, где компьютер хранит полное описание каждого элемента изображения, при фрактальном подходе хранится лишь формула или алгоритм создания объекта. Это значительно экономит память и вычислительные ресурсы, особенно при работе со сложными объектами. Например, для создания реалистичного дерева достаточно задать алгоритм ветвления и несколько базовых параметров вместо детального описания каждой ветви и листа.
В киноиндустрии фрактальные алгоритмы используются для генерации впечатляющих спецэффектов и фантастических ландшафтов. Такие блокбастеры, как «Звездные войны», «Аватар» и многие научно-фантастические фильмы, широко используют фрактальные технологии для создания инопланетных пейзажей, космических облаков и других визуальных элементов, которые было бы чрезвычайно трудоемко моделировать вручную.
Фрактальное сжатие изображений представляет собой еще одно перспективное применение, хотя и менее распространенное сегодня. Этот метод использует самоподобие в изображениях для их эффективного кодирования, потенциально обеспечивая высокие коэффициенты сжатия, особенно для фотографий природных объектов.
В области визуализации данных фрактальные методы помогают выявлять скрытые закономерности в больших наборах информации, представляя их в интуитивно понятной графической форме. Такие визуализации позволяют аналитикам обнаруживать паттерны и аномалии, которые могут быть неочевидны при традиционном статистическом анализе.
Моделирование природных процессов
В области моделирования природных процессов фрактальная геометрия предоставляет мощный инструментарий, который кардинально изменил подход ученых к пониманию и прогнозированию сложных природных явлений. Традиционные методы, основанные на дифференциальных уравнениях, часто оказываются недостаточными для описания нерегулярных, хаотичных процессов, которыми изобилует природа.
Метеорология и климатология стали одними из первых областей, где фрактальные модели продемонстрировали свою эффективность. Атмосферные явления, такие как формирование облаков, распространение воздушных масс и турбулентные потоки, обладают фрактальной структурой на различных масштабах. Современные компьютерные модели прогнозирования погоды используют фрактальные алгоритмы для более точного моделирования динамики атмосферы, что значительно повышает точность прогнозов, особенно в долгосрочной перспективе.
В гидрологии фрактальные модели применяются для описания речных систем, распределения осадков и паводков. Река со всеми её притоками представляет собой естественную фрактальную структуру, и понимание этой закономерности позволяет более точно прогнозировать поведение водных систем при различных условиях.
Особенно впечатляющие результаты фрактальное моделирование демонстрирует при воссоздании рельефа местности. Алгоритмы, основанные на фрактальной геометрии, способны генерировать реалистичные ландшафты с горными хребтами, долинами, эрозионными узорами и другими естественными особенностями, которые на первый взгляд кажутся неупорядоченными, но в действительности подчиняются фрактальным закономерностям.
Заключение: Почему фракталы важны?
Фрактальная геометрия представляет собой нечто большее, чем просто красивые математические объекты или инструмент для создания впечатляющей компьютерной графики. Она предлагает фундаментально новый способ понимания мира, преодолевая ограничения евклидовой геометрии, которая доминировала в науке на протяжении тысячелетий.
В мире, где реальные объекты редко имеют форму идеальных линий, квадратов и окружностей, фракталы предоставляют язык для описания сложности, нерегулярности и хаоса, которые мы наблюдаем повсюду — от микроскопических биологических структур до галактических скоплений. Они позволяют нам увидеть порядок в кажущемся беспорядке, выявить закономерности там, где раньше мы видели лишь случайность.
Значимость фракталов выходит далеко за пределы чисто теоретического интереса. Они становятся инструментом для моделирования и прогнозирования поведения сложных систем во множестве дисциплин — от метеорологии до медицины, от экономики до экологии. Причем эти модели не только эффективны, но и элегантны в своей математической простоте, демонстрируя, как сложное может возникать из простого через итерации и самоподобие.
Возможно, самый важный урок, который дают нам фракталы, заключается в том, что для понимания сложности не всегда требуются сложные объяснения. Иногда богатство и многообразие форм могут возникать из удивительно простых правил, повторяемых снова и снова на разных масштабах. Это напоминает нам о фундаментальном единстве природы и математики — связи, которая продолжает вдохновлять и удивлять как ученых, так и людей искусства.

Почему одни бренды помнят все, а другие — никто?
Узнаваемость бренда — это не просто модный термин, а реальный инструмент роста. Как сделать так, чтобы ваше имя первым всплывало в голове клиента? В этой статье — конкретные примеры, советы и метрики.

Django — что это такое, как работает и зачем нужен разработчику
Django Python — что это и почему этот фреймворк так часто выбирают для крупных проектов? В статье разберём архитектуру, возможности и реальные сценарии применения, чтобы вы поняли, подходит ли он именно вам.
Что такое DOM, как он устроен и как с ним работать
Объектная модель документа dom — это основа всей интерактивности в вебе, но как именно она устроена? В этом материале разберём, как браузер превращает HTML в DOM-дерево и как с ним работает JavaScript на практике.

Что такое репутационный менеджмент и почему он важен каждой компании
Репутационный менеджмент — это не про «глянцевую обложку», а про контроль восприятия бизнеса. Что делает стратегию устойчивой, а ошибки — фатальными?