Зачем программисту знать, как работает алгоритм из 1956 года?
Каждый раз, когда вы прокладываете маршрут в навигаторе, ваш смартфон решает весьма нетривиальную задачу поиска оптимального пути. Под капотом этого процесса часто скрывается алгоритм Дейкстры — элегантное решение, придуманное голландским учёным за чашкой кофе. Этот математический метод позволяет находить кратчайшие пути в графах и лежит в основе множества современных технологий: от навигационных систем и компьютерных сетей до искусственного интеллекта в играх.

В этой статье мы разберёмся, как работает algorithm Дейкстры, почему он так важен и где применяется в реальном мире, попутно прояснив, почему навигатор иногда ведёт вас странными маршрутами.
- Что такое алгоритм Дейкстры и зачем он нужен
- Как работает алгоритм Дейкстры (пошаговое объяснение)
- Основные понятия и определения
- Принцип работы алгоритма
- Пояснение на простом примере
- Пошаговый разбор на примере (таблица или схема)
- Где применяется алгоритм Дейкстры в реальной жизни
- Онлайн-карты и навигация
- Компьютерные сети и маршрутизация
- Игровая индустрия и AI
- Логистика и системы бронирования
- Ограничения алгоритма
- Алгоритм Дейкстры в коде (бонус-раздел для разработчиков)
- Используемые структуры данных
- Минимальная реализация на Python
- Заключение
Что такое алгоритм Дейкстры и зачем он нужен
Алгоритм Дейкстры — это метод поиска кратчайшего пути от одной вершины графа ко всем остальным. Если перевести с сухого математического на человеческий, это способ найти самый короткий маршрут от точки А до всех возможных точек назначения. При этом «короткий» может означать не только расстояние в километрах, но и время, стоимость, количество потраченных нервных клеток в пробке — в общем, любой параметр, который можно измерить числом.
Придумал это чудо в 1956 году голландский учёный Эдсгер Дейкстра, когда искал способ продемонстрировать возможности нового компьютера ARMAC (да-да, тогда компьютеры ещё были размером с комнату и работали на перфокартах). По его собственному признанию, решение пришло к нему за чашкой кофе в амстердамском кафе всего за 20 минут — что называется, вдохновение может настигнуть где угодно.
«Одна из причин, по которой algorithm получился таким красивым, заключалась в том, что я создал его в уме, без карандаша и бумаги. Позже я узнал, что одно из преимуществ такого проектирования состоит в том, что при этом вы стараетесь максимально избегать сложностей.» — Эдсгер Дейкстра.
Сегодня этот алгоритм используется повсеместно:
- В навигационных системах, чтобы вы могли попасть из точки А в точку Б, минуя все дорожные работы
- В компьютерных сетях для маршрутизации данных (привет, ваши мемы и посты доходят до адресата благодаря в том числе и Дейкстре)
- В игровой индустрии, где NPC должны найти путь к игроку, чтобы его… эм… поприветствовать
- В логистике для оптимизации доставки грузов
- В системах бронирования для поиска оптимальных маршрутов с пересадками
Зачем это нужно разработчику:
Понимание algorithm Дейкстры — базовый навык для любого программиста, который хочет решать задачи оптимизации маршрутов, работать с графами или создавать искусственный интеллект для игр. Кроме того, это один из тех алгоритмов, который постоянно всплывает на собеседованиях, особенно если вы претендуете на позиции, связанные с бэкендом, анализом данных или геймдевом.
Как работает алгоритм Дейкстры (пошаговое объяснение)
Основные понятия и определения
Прежде чем погрузиться в пучину алгоритмических страстей, давайте разберёмся с терминологией — без неё мы будем как туристы без карты в лабиринте Минотавра.
Граф — это такая математическая структура, состоящая из vertex (узлов) и рёбер (связей) между ними. Представьте себе карту метро: станции — это vertex, а линии между ними — рёбра. Или социальную сеть, где пользователи — вершины, а дружеские связи — рёбра. В общем, граф — это способ моделировать взаимосвязи между объектами (которые, к счастью, не обязательно должны быть людьми, иначе социальные графы были бы ещё более запутанными, чем они есть).
Вершина — это точка, узел, элемент графа. В контексте навигатора — это может быть перекрёсток, достопримечательность или тот подозрительный поворот, где вы всегда сворачиваете не туда.
Ребро — связь между vertex. В нашем случае — дорога, соединяющая два пункта. Рёбра могут быть направленными (односторонний проезд) или ненаправленными (движение в обе стороны).
Вес ребра — это число, характеризующее «стоимость» перемещения по ребру. Может выражаться в километрах, минутах, рублях за проезд или количестве нецензурных выражений, которые вы произнесёте, застряв в пробке на этом участке.
Взвешенный граф — граф, в котором каждому ребру присвоен некоторый вес. Именно с такими графами работает algorithm Дейкстры — он не может функционировать с рёбрами без веса или (что ещё хуже) с отрицательными весами (хотя, кто не мечтал о дороге с отрицательной длиной, по которой чем дальше едешь, тем ближе становишься к цели).
Принцип работы алгоритма
Алгоритм Дейкстры работает по принципу «жадной» стратегии — на каждом шаге он выбирает наиболее выгодное решение, не задумываясь о долгосрочной перспективе (прямо как я в молодости). Удивительно, но для задачи поиска кратчайшего пути такой подход даёт оптимальный результат.
Вот как это происходит на словах:
- Мы назначаем стартовой вершине расстояние 0, а всем остальным — бесконечность (что символизирует наше полное неведение о том, как до них добраться).
- Помечаем все vertex как непосещённые и создаём список всех непосещённых vertex.
- Для текущей вершины (изначально — стартовой) рассматриваем все соседние непосещённые vertex и вычисляем их предварительные расстояния. Если вычисленное distance меньше уже записанного, перезаписываем его.
- Когда мы обработали все соседние vertex, помечаем текущую vertex как посещённую и удаляем её из списка непосещённых. Посещённая вершина больше никогда не будет проверяться (как экс, которого вы поклялись больше никогда не вспоминать).
- Если конечная vertex помечена как посещённая или если наименьшее расстояние между непосещёнными vertex равно бесконечности — останавливаемся.
- Иначе выбираем непосещённую вершину с наименьшим distance в качестве новой текущей и повторяем с шага 3.
Звучит сложно? Поверьте, на практике всё гораздо запутаннее! Шучу, сейчас мы разберём это на примере, и всё станет кристально ясно (ну, или почти).
Пояснение на простом примере
Допустим, у нас есть граф городов, соединённых дорогами. Назовём их A, B, C, D, E, F. Числа возле рёбер — расстояния между городами в километрах. Нам нужно найти кратчайший путь от города A до всех остальных городов.
Этапы работы algorithm:
- Инициализация: distance до A = 0, до всех остальных = ∞
- Текущая vertex = A. Смотрим соседей: B (7 км) и E (4 км). Обновляем их расстояния.
- Помечаем A как посещённую.
- Выбираем вершину с минимальным distance — E (4 км).
- Смотрим соседей E: F (7 км = 4+3) и D (12 км = 4+8). Обновляем их расстояния.
- Помечаем E как посещённую.
- Выбираем vertex с минимальным distance — B (7 км).
- И так далее, пока не обработаем все vertex.
В итоге мы получим кратчайшие пути от A до каждой vertex:
- A→B: 7 км
- A→C: через B: 10 км (7+3)
- A→D: через E: 12 км (4+8)
- A→E: 4 км
- A→F: через E: 7 км (4+3)
Теперь, когда вы видите, как это работает на практике, можно понять, почему данный алгоритм так широко используется — он эффективно находит оптимальные пути, не перебирая все возможные варианты (что было бы катастрофически долго даже для небольших графов).
Пошаговый разбор на примере (таблица или схема)
Давайте разберём работу algorithm Дейкстры на конкретном примере с визуализацией каждого шага. Для наглядности я возьму небольшой граф из 6 vertex, обозначенных буквами от A до F, со следующими связями и весами:
| Связь | Вес |
|---|---|
| A-B | 4 |
| A-C | 7 |
| B-D | 2 |
| B-E | 8 |
| C-D | 2 |
| C-E | 5 |
| D-E | 1 |
| D-F | 4 |
| E-F | 11 |
Наша задача — найти кратчайшие пути от vertex A до всех остальных.
Шаг 0: Инициализация
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Нет | — |
| B | ∞ | Нет | — |
| C | ∞ | Нет | — |
| D | ∞ | Нет | — |
| E | ∞ | Нет | — |
| F | ∞ | Нет | — |
🧠 Комментарий: На старте мы знаем только distance до начальной вершины A (оно равно 0). О расстояниях до остальных vertex нам ничего не известно, поэтому ставим бесконечность.
Шаг 1: Выбираем вершину A (непосещённую с минимальным расстоянием)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Нет | A |
| C | 7 | Нет | A |
| D | ∞ | Нет | — |
| E | ∞ | Нет | — |
| F | ∞ | Нет | — |
🧠 Комментарий: Мы обрабатываем вершину A, смотрим на её соседей (B и C) и обновляем distance до них. От A до B — 4, от A до C — 7. Помечаем A как посещённую.
Шаг 2: Выбираем вершину B (непосещённую с минимальным расстоянием)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Да | A |
| C | 7 | Нет | A |
| D | 6 | Нет | B |
| E | 12 | Нет | B |
| F | ∞ | Нет | — |
🧠 Комментарий: Обрабатываем B (ближайшую непосещённую vertex). Смотрим на соседей B — это D и E. Расстояние до D через B: 4 + 2 = 6. Расстояние до E через B: 4 + 8 = 12. Обновляем таблицу и помечаем B как посещённую.
Шаг 3: Выбираем вершину D (непосещённую с минимальным расстоянием)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Да | A |
| C | 7 | Нет | A |
| D | 6 | Да | B |
| E | 7 | Нет | D |
| F | 10 | Нет | D |
🧠 Комментарий: Теперь ближайшая непосещённая vertex — D (distance 6). Соседи D — это E и F. Расстояние до E через D: 6 + 1 = 7, что меньше предыдущего значения (12), поэтому обновляем. Расстояние до F через D: 6 + 4 = 10. Помечаем D как посещённую.
Шаг 4: Выбираем вершину C (непосещённую с минимальным расстоянием)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Да | A |
| C | 7 | Да | A |
| D | 6 | Да | B |
| E | 7 | Нет | D |
| F | 10 | Нет | D |
🧠 Комментарий: C и E имеют одинаковое distance (7), но выберем C (порядок не важен, если distance равны). Соседи C — D и E. Расстояние до D через C: 7 + 2 = 9, что больше текущего (6), поэтому не обновляем. Расстояние до E через C: 7 + 5 = 12, что больше текущего (7), поэтому тоже не обновляем. Помечаем C как посещённую.
Шаг 5: Выбираем вершину E (непосещённую с минимальным расстоянием)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Да | A |
| C | 7 | Да | A |
| D | 6 | Да | B |
| E | 7 | Да | D |
| F | 10 | Нет | D |
🧠 Комментарий: Обрабатываем E. Единственный непосещённый сосед E — это F. Расстояние до F через E: 7 + 11 = 18, что больше текущего (10), поэтому не обновляем. Помечаем E как посещённую.
Шаг 6: Выбираем вершину F (последнюю непосещённую)
| Вершина | Расстояние от A | Посещена | Предыдущая вершина |
|---|---|---|---|
| A | 0 | Да | — |
| B | 4 | Да | A |
| C | 7 | Да | A |
| D | 6 | Да | B |
| E | 7 | Да | D |
| F | 10 | Да | D |
🧠 Комментарий: У F нет непосещённых соседей. Помечаем F как посещённую. Алгоритм завершён!
✅ Итоговые кратчайшие пути от A:
- До A: 0 (A)
- До B: 4 (A → B)
- До C: 7 (A → C)
- До D: 6 (A → B → D)
- До E: 7 (A → B → D → E)
- До F: 10 (A → B → D → F)
Обратите внимание, что путь A → B → D → E (7) короче, чем путь A → C → E (12) или A → B → E (12). Алгоритм Дейкстры правильно определил оптимальный маршрут, что очень впечатляет для algorithm, который мог быть придуман за чашкой кофе!
Это демонстрирует мощь алгоритма: для каждой вершины мы получаем не только минимальное distance от стартовой точки, но и предыдущую vertex на этом пути, что позволяет нам восстановить весь маршрут целиком (в отличие от навигаторов, которые иногда стесняются показать полный маршрут до того, как вы первый раз свернёте не туда).
Где применяется алгоритм Дейкстры в реальной жизни
Алгоритм Дейкстры — это один из тех математических инструментов, который незримо присутствует в нашей повседневной жизни, как назойливый родственник, который всегда оказывается рядом, когда вы меньше всего этого ожидаете. Рассмотрим основные сферы, где этот algorithm заставляет мир крутиться чуть быстрее (или, по крайней мере, оптимальнее).
Онлайн-карты и навигация
Каждый раз, когда вы открываете Google Maps, Яндекс.Навигатор или любое другое приложение для построения маршрутов, за кулисами происходит настоящее магическое представление с участием алгоритма Дейкстры (или его продвинутых модификаций).
✔ Примеры использования:
- Построение оптимального автомобильного маршрута с учетом пробок, ремонтных работ и времени суток
- Прокладка пешеходных маршрутов с обходом закрытых переходов и парков
- Расчет велосипедных треков с минимальными перепадами высот
- Построение мультимодальных маршрутов (например, сначала на автобусе, потом пешком, затем на метро)
Забавный факт: когда навигатор вдруг решает направить вас через какие-то подозрительные дворы вместо главной дороги — это не потому, что он хочет познакомить вас с местной шпаной, а потому что algorithm нашел там реальное сокращение пути или времени. Хотя, конечно, есть нюанс — навигатор не учитывает фактор «стрёмности» района.
Компьютерные сети и маршрутизация
В мире компьютерных сетей алгоритм Дейкстры — настоящая звезда. Он используется в протоколах маршрутизации, которые определяют, как данные будут передаваться от одного устройства к другому.
✔ Примеры использования:
- Протокол OSPF (Open Shortest Path First) — использует модифицированный алгоритм Дейкстры для нахождения кратчайших путей между маршрутизаторами
- Протокол IS-IS (Intermediate System to Intermediate System) — также основан на algorithm Дейкстры
- Расчет топологии сети для оптимальной передачи данных
- Балансировка нагрузки в распределенных системах
Когда вы отправляете сообщение или открываете веб-страницу, данные часто проходят через десятки маршрутизаторов, выбирающих путь благодаря нашему голландскому гению. И всё это происходит так быстро, что вы успеваете проскроллить ленту инстаграма, пока ждёте свой кофе.
Игровая индустрия и AI
Если вы когда-нибудь играли в компьютерные игры, то наверняка замечали, что неигровые персонажи (NPC) обычно довольно неплохо находят к вам дорогу, чтобы… эм… поприветствовать. Это заслуга algorithm поиска пути, включая алгоритм Дейкстры и его «потомков».
✔ Примеры использования:
- Перемещение NPC в открытом мире (например, в RPG или стратегиях)
- Поиск пути для юнитов в стратегических играх
- Построение маршрутов для автомобилей в гоночных симуляторах
- Расчет оптимальных тактик в играх с искусственным интеллектом
В некоторых играх algorithm даже модифицируют так, чтобы враги иногда специально выбирали не самый короткий путь — для создания иллюзии человеческого поведения и непредсказуемости. Потому что идеальная эффективность — это подозрительно и немного жутковато (как, впрочем, и люди, всегда выбирающие оптимальные решения).
Логистика и системы бронирования
В мире логистики и транспорта алгоритм Дейкстры — незаменимый инструмент для оптимизации перемещений и расходов.
✔ Примеры использования:
- Планирование маршрутов доставки для курьерских служб и грузоперевозок
- Оптимизация маршрутов общественного транспорта
- Системы бронирования авиабилетов с поиском оптимальных пересадок
- Расчет маршрутов для роботов на автоматизированных складах
Когда вы заказываете доставку еды и приложение сообщает, что курьер будет через 30 минут — это не просто грубая оценка, а результат сложных расчетов, учитывающих трафик, distance и даже особенности конкретного района. Хотя, конечно, сложно предсказать, когда курьер решит сделать перекур или заблудится в лабиринте вашего ЖК.
Алгоритм Дейкстры, несмотря на свою солидную возрастную категорию (ему уже за 60!), продолжает оставаться актуальным и востребованным в современных технологиях. Даже с появлением более современных algorithm вроде A*, он остаётся золотым стандартом для многих практических задач — как тот дядюшка, который хоть и старомоден, но всегда даёт дельные советы.
Ограничения алгоритма
Как и любой инструмент, созданный человеком (за исключением, пожалуй, швейцарского ножа, который действительно универсален), algorithm Дейкстры имеет свой набор ограничений и слабых мест. Знание этих ограничений поможет избежать нелепых ситуаций, когда ваше приложение внезапно решает, что оптимальный путь к холодильнику лежит через соседний город.
✔ Основные проблемные случаи:
- Графы с отрицательными весами — главная ахиллесова пята алгоритма. Дейкстра категорически отказывается работать с графами, где некоторые рёбра имеют отрицательный вес. Это как если бы вы попытались скормить вегану стейк — реакция будет непредсказуемой и потенциально разрушительной. При наличии отрицательных весов algorithm может зациклиться или выдать неверный результат, потому что он основан на предположении, что, пройдя по ребру, мы никогда не уменьшим общее distance.
- Большие графы без оптимизаций — стандартная реализация алгоритма Дейкстры работает со сложностью O(n²), где n — количество вершин. Для графа с миллионом вершин (например, карта большого города) это примерно триллион операций — ваш смартфон скорее устанет от жизни, чем закончит расчёт. Поэтому для больших графов используют оптимизированные версии algorithm с применением специальных структур данных (например, двоичных куч), что снижает сложность до O(m log n), где m — количество рёбер.
- Динамически изменяющиеся графы — если в процессе работы алгоритма веса рёбер меняются (например, из-за появления пробки на дороге), Дейкстра не сможет автоматически адаптироваться. Представьте, что вы построили маршрут до работы, а посреди дороги узнаёте, что впереди авария — algorithm придётся пересчитывать путь с учётом новых обстоятельств.
- Высокие требования к памяти — для больших графов алгоритм требует значительных ресурсов памяти для хранения информации о расстояниях, посещённых vertex и предшественниках. Это особенно актуально для мобильных устройств или встраиваемых систем с ограниченными ресурсами.
- Отсутствие эвристик — algorithm Дейкстры рассматривает все направления равномерно, что может быть неэффективно, если мы примерно знаем, где находится цель. Это как если бы вы искали иголку в стоге сена, методично проверяя каждую соломинку, вместо того чтобы использовать магнит.
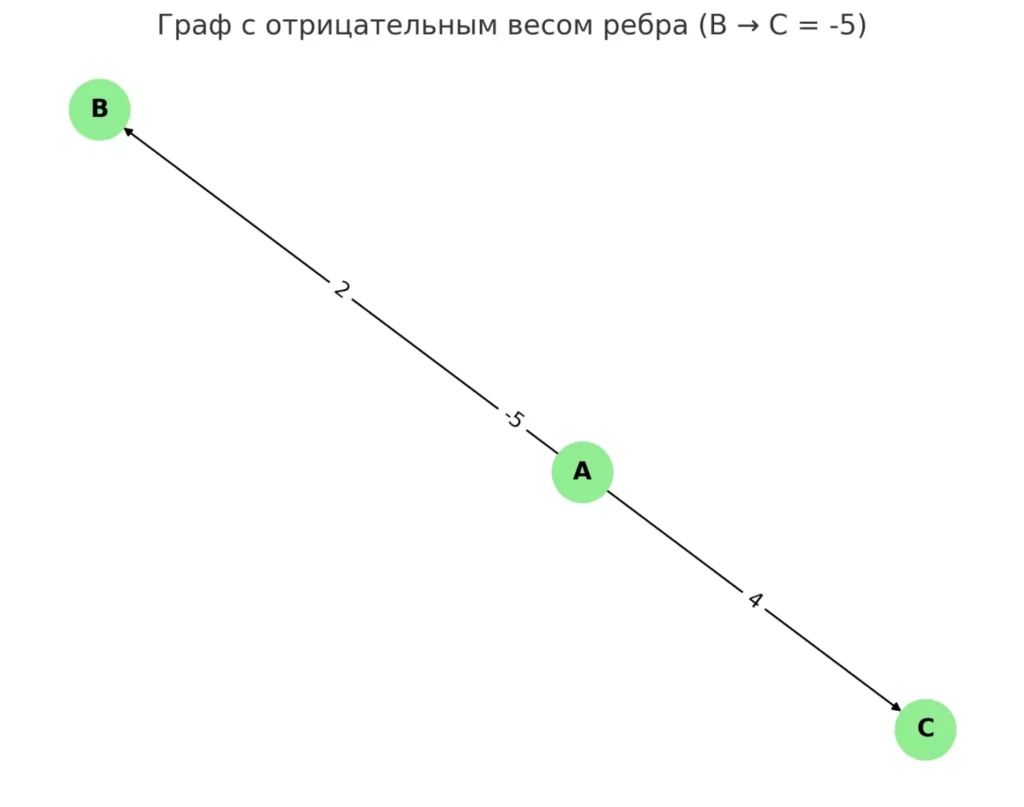
Визуализация графа с отрицательным весом ребра (B → C = -5)
Альтернативы алгоритму Дейкстры:
Когда Дейкстра пасует, на сцену выходят другие algorithm:
- Алгоритм Беллмана-Форда справляется с графами, содержащими рёбра с отрицательным весом, но платит за это увеличением временной сложности до O(nm).
- Алгоритм A* (A-звезда) использует эвристическую функцию для направленного поиска, что делает его значительно более эффективным в ситуациях, когда мы знаем примерное направление к цели (например, в навигации или компьютерных играх).
- Алгоритм Флойда-Уоршелла находит кратчайшие пути между всеми парами вершин в графе за O(n³), что может быть эффективнее запуска algorithm Дейкстры из каждой vertex для плотных графов.
Выбор алгоритма зависит от конкретной задачи, размера графа и наличия специфических требований. Как говорится, нет универсального инструмента — каждая отвёртка хороша для своего шурупа (хотя, признаюсь, я иногда использую отвёртку и как рычаг, и как молоток, и даже как открывашку для бутылок, но это уже совсем другая история).
Алгоритм Дейкстры в коде (бонус-раздел для разработчиков)
Теперь давайте перейдем от теории к практике и посмотрим, как реализовать этот математический шедевр в коде. Я выбрал Python как язык реализации — не потому, что он самый эффективный для этой задачи (спойлер: не самый), а потому что он наиболее читаемый даже для тех, кто обычно программирует на своем естественном языке жестами и нецензурными комментариями.
Используемые структуры данных
Для реализации algorithm Дейкстры нам понадобятся:
- Граф — представим его в виде словаря, где ключи — вершины, а значения — словари с соседними vertex и весами рёбер.
- Массив расстояний — словарь, хранящий текущие кратчайшие distance от стартовой вершины до всех остальных.
- Приоритетная очередь — для эффективного выбора vertex с минимальным distance. В Python для этого удобно использовать модуль heapq.
Минимальная реализация на Python
import heapq
def dijkstra(graph, start):
# Инициализация словаря для хранения расстояний
# до каждой вершины. Сначала все расстояния бесконечны.
distances = {vertex: float('infinity') for vertex in graph}
# Расстояние до начальной вершины равно 0
distances[start] = 0
# Словарь для хранения предшественников (для восстановления пути)
predecessors = {vertex: None for vertex in graph}
# Приоритетная очередь для хранения вершин и их расстояний
priority_queue = [(0, start)]
while priority_queue:
# Извлекаем вершину с наименьшим расстоянием из очереди
current_distance, current_vertex = heapq.heappop(priority_queue)
# Если текущее расстояние больше, чем уже известное, пропускаем
if current_distance > distances[current_vertex]:
continue
# Проходим по всем соседям текущей вершины
for neighbor, weight in graph[current_vertex].items():
# Вычисляем новое расстояние
distance = current_distance + weight
# Если найден более короткий путь, обновляем расстояние
if distance < distances[neighbor]: distances[neighbor] = distance predecessors[neighbor] = current_vertex # Добавляем в очередь для дальнейшего рассмотрения heapq.heappush(priority_queue, (distance, neighbor)) return distances, predecessors # Пример использования if __name__ == "__main__": # Наш граф из примера выше graph = { 'A': {'B': 4, 'C': 7}, 'B': {'A': 4, 'D': 2, 'E': 8}, 'C': {'A': 7, 'D': 2, 'E': 5}, 'D': {'B': 2, 'C': 2, 'E': 1, 'F': 4}, 'E': {'B': 8, 'C': 5, 'D': 1, 'F': 11}, 'F': {'D': 4, 'E': 11} } distances, predecessors = dijkstra(graph, 'A') # Вывод результата print("Кратчайшие расстояния от вершины A:") for vertex, distance in distances.items(): print(f"До {vertex}: {distance}") # Восстановление пути до конкретной вершины (например, F) def get_path(predecessors, target): path = [] current = target while current: path.append(current) current = predecessors[current] return path[::-1] # Разворачиваем путь print("\nКратчайший путь от A до F:", " -> ".join(get_path(predecessors, 'F')))
Этот код реализует алгоритм Дейкстры с использованием приоритетной очереди для улучшения производительности. Временная сложность этой реализации — O((n + m) log n), где n — количество вершин, m — количество рёбер.
Обратите внимание на функцию get_path — она позволяет восстановить конкретный маршрут от стартовой вершины до указанной. Это важно, потому что сам algorithm выдаёт только distance и предшественников, но не готовый маршрут (как навигатор, который знает, как доехать до пункта назначения, но не хочет делиться этой информацией, пока вы не начнёте движение).
В реальных приложениях, конечно, эта базовая реализация обрастает дополнительной функциональностью: обработкой ошибок, оптимизациями для конкретных типов графов, возможностью учитывать дополнительные ограничения (например, избегать определённых типов дорог) и так далее. Но суть остаётся прежней — стартуем из одной точки и шаг за шагом расширяем наше «дерево» оптимальных путей, пока не охватим весь граф или не достигнем цели.
Заключение
Алгоритм Дейкстры — один из тех редких случаев, когда математический метод, придуманный за чашкой кофе в амстердамском кафе, находит применение в миллиардах электронных устройств по всему миру. От навигационных систем, определяющих ваш маршрут на работу, до маршрутизаторов, пересылающих ваши данные по интернету, и искусственного интеллекта в компьютерных играх — этот algorithm остаётся фундаментальным инструментом для решения задач оптимизации маршрутов.
Понимание алгоритма Дейкстры — это не просто академическое упражнение для студентов компьютерных специальностей. Это практический навык, который может пригодиться в самых разных областях: от проектирования сетей и разработки игр до анализа данных и логистики. Более того, сам подход «жадного» algorithm, лежащий в его основе, может быть применён к широкому кругу задач оптимизации.
Несмотря на свои ограничения (работает только с положительными весами, может быть неэффективен для очень больших графов без оптимизаций), алгоритм Дейкстры остаётся золотым стандартом благодаря своей простоте и надёжности. А его многочисленные модификации и дополнения, такие как algorithm A*, позволяют обходить эти ограничения в случаях, когда это необходимо.
Так что в следующий раз, когда ваш навигатор проложит маршрут через дворы, вместо того чтобы проклинать технологии, вспомните о голландском учёном, который за 20 минут придумал алгоритм, изменивший мир навигации навсегда. Хотя, конечно, за проезд через эти самые дворы проклинать технологии всё-таки можно — алгоритм Дейкстры, при всей своей гениальности, не учитывает, что некоторые «оптимальные» маршруты лучше оставить теоретикам.

Многопоточность в Android: полное руководство
Android многопоточность — тема, без которой невозможно создавать быстрые и удобные приложения. Хотите понять, как грамотно распределять задачи и избегать зависаний? В этом материале мы разложим всё по полочкам и дадим простые советы.

Ручная или автоматизированная верстка: что лучше для вашего сайта?
Ручная верстка или автоматизированные конструкторы? Разберемся, какой метод лучше подходит для сложных задач, SEO и креативного дизайна.

Edge computing: новый подход к обработке данных
Узнайте, как edge computing помогает обрабатывать данные ближе к источнику. Архитектура, ключевые технологии и практическое применение – всё это в нашей статье.

Adobe XD — что это, возможности и особенности работы с инструментом
Знаете ли вы, почему многие дизайнеры переходят с Photoshop на Adobe XD? В этой статье вы узнаете, как создавать прототипы сайтов и приложений, тестировать UX и работать в команде без лишних инструментов.