Числа, которые видят все, но понимают не все
Математические закономерности окружают нас повсюду, но некоторые из них заслуживают особого внимания. Среди таких феноменов — числа Фибоначчи, которые мы встречаем гораздо чаще, чем можем представить. Эта последовательность, выведенная итальянским математиком более восьми веков назад, оказалась настолько универсальной, что проникла во все сферы нашей жизни: от природных форм и художественных композиций до финансовых моделей и программных алгоритмов.

В этой статье мы рассмотрим, почему числа fibonacci продолжают играть значительную роль в современном мире, несмотря на свой почтенный возраст. Мы раскроем их математическую сущность, исследуем исторический контекст их появления и разберемся, как эта простая на первый взгляд последовательность связана с понятием золотого сечения — пропорцией, которую часто называют формулой красоты. Особое внимание уделим практическому применению этих чисел: от анализа природных структур и создания эстетически привлекательных дизайнов до программирования и даже биржевой торговли. Давайте вместе погрузимся в мир Фибоначчи, который выходит далеко за рамки классического примера с кроликами.
- Что такое числа Фибоначчи
- Немного истории: от Пизы до Python
- Задача о кроликах Фибоначчи
- Как числа Фибоначчи связаны с золотым сечением
- Примеры чисел Фибоначчи в природе и искусстве
- В растениях и живых организмах
- В архитектуре и искусстве
- Зачем программистам нужны числа Фибоначчи
- Пример рекурсивной функции на Python
- Где ещё применяется
- Фибоначчи в трейдинге: правда или миф?
- Почему числа Фибоначчи не всегда работают (и это нормально)
- Краткий вывод: зачем нам все эти Фибоначчи
Что такое числа Фибоначчи
На первый взгляд, числа fibonacci представляют собой лишь последовательность чисел, построенную по определённому правилу. Однако за этой внешней простотой скрывается математическая закономерность, обладающая удивительными свойствами и находящая применение в самых разных областях.
Последовательность Фибоначчи строится по следующему принципу: каждое последующее число равно сумме двух предыдущих. Математически это можно выразить простой формулой:
F(n) = F(n-1) + F(n-2), где F(0) = 0, F(1) = 1 для n ≥ 2
В некоторых источниках последовательность начинается с пары чисел 1, 1, но классический вариант, описанный самим fibonacci, стартует с 0 и 1. Если представить первые элементы этого ряда, то они выглядят следующим образом:
- 0
- 1
- 1 (0 + 1)
- 2 (1 + 1)
- 3 (1 + 2)
- 5 (2 + 3)
- 8 (3 + 5)
- 13 (5 + 8)
- 21 (8 + 13)
- 34 (13 + 21)
- 55 (21 + 34)
- 89 (34 + 55)
- 144 (55 + 89)
- 233 (89 + 144)
- 377 (144 + 233)
Примечательно, что чем дальше мы продвигаемся по этой последовательности, тем более интересные закономерности начинают проявляться. И дело не только в правиле сложения — числа Фибоначчи обладают множеством уникальных математических свойств, которые делают их ценным инструментом как для теоретических исследований, так и для решения практических задач в различных областях науки и техники.
Немного истории: от Пизы до Python
История чисел fibonacci начинается в средневековой Италии XIII века, когда математик Леонардо Пизанский (более известный под прозвищем Фибоначчи) опубликовал свой фундаментальный труд «Liber Abaci» («Книга абака» или «Книга вычислений»). Этот научный трактат, изданный в 1202 году, стал революционным для европейской математики, поскольку в нём Леонардо познакомил западный мир с арабскими цифрами и десятичной системой счисления, которые были гораздо удобнее римских цифр, использовавшихся в то время.
Парадоксально, но сама последовательность fibonacci появилась в книге не как серьёзное математическое открытие, а скорее как иллюстрация к одной из задач — ныне знаменитой «задаче о кроликах». В ней Леонардо описал гипотетическую ситуацию размножения кроликов при определённых условиях.
Задача о кроликах Фибоначчи
В загон помещена пара новорождённых кроликов (самец и самка). Кролики начинают производить потомство по достижении двухмесячного возраста, принося каждый месяц новую пару (самца и самку). Предполагается, что кролики бессмертны и всегда производят потомство по указанному правилу. Требуется определить, сколько пар кроликов будет через год.
Для решения этой задачи Леонардо вывел последовательность, где каждый член соответствовал количеству пар кроликов в определённый месяц. При заданных условиях через 12 месяцев в загоне должно было оказаться 233 пары.
Хотя эта последовательность стала известна под именем fibonacci, справедливости ради стоит отметить, что она была известна задолго до него. Древнеиндийские математики применяли её для анализа поэтических размеров ещё в VI веке. Заслуга Фибоначчи состоит в том, что он не только популяризировал её в Европе, но и связал с практическими задачами, заложив основу для её дальнейшего изучения.
Сегодня, спустя восемь веков, последовательность fibonacci остаётся одной из самых изучаемых в математике, а её реализация на различных языках программирования, включая современный Python, стала классическим примером при обучении рекурсивным алгоритмам.
Как числа Фибоначчи связаны с золотым сечением
Одно из самых удивительных свойств последовательности fibonacci — её тесная связь с золотым сечением, или числом φ (фи), приблизительно равным 1,618. Эта связь настолько фундаментальна, что позволяет нам рассматривать числа Фибоначчи как прикладной инструмент для реализации золотой пропорции в различных областях — от искусства до дизайна интерфейсов.
Математически связь между числами fibonacci и золотым сечением выражается в том, что отношение каждого числа последовательности к предыдущему стремится к золотому сечению при увеличении номера числа. Иными словами, если мы рассмотрим достаточно большие числа Фибоначчи, то их соотношение будет всё ближе и ближе подходить к значению φ.
Давайте проследим, как это происходит:
| Отношение | Вычисление | Значение | Приближение к φ |
|---|---|---|---|
| F(3)/F(2) | 2/1 | 2 | Далеко от φ |
| F(5)/F(4) | 5/3 | 1,667 | Ближе к φ |
| F(8)/F(7) | 21/13 | 1,615 | Еще ближе к φ |
| F(12)/F(11) | 144/89 | 1,6180 | Очень близко к φ |
| F(∞)/F(∞-1) | — | 1,6180339887… | Золотое сечение φ |
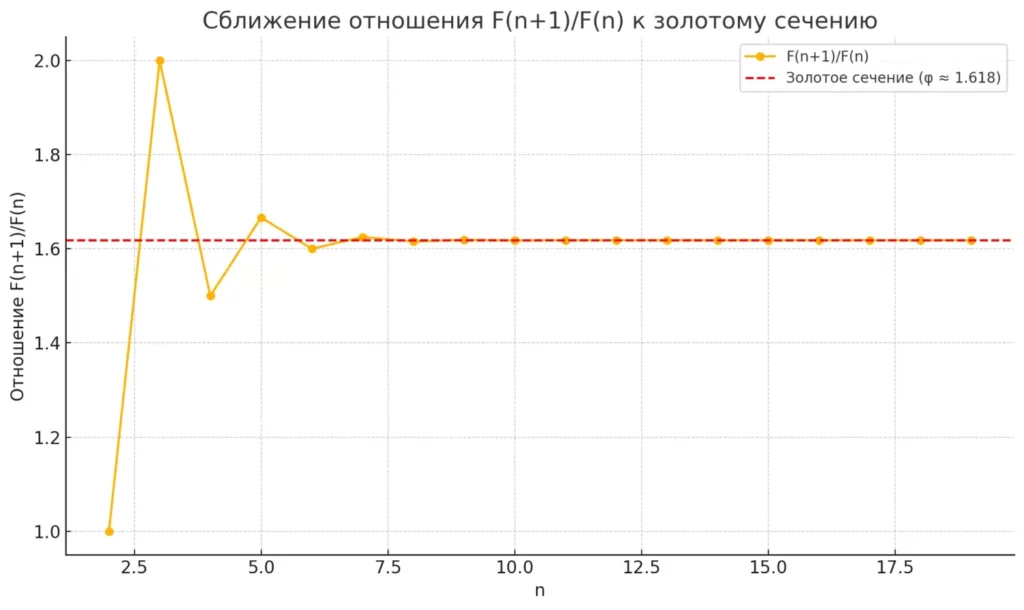
Визуализация, демонстрирующая, как отношение соседних чисел Фибоначчи стремится к числу золотого сечения (φ ≈ 1.618) по мере роста номера элемента
Чем дальше мы продвигаемся по последовательности fibonacci, тем точнее становится это приближение. Математически это можно выразить как:
| n | F(n) | F(n+1) | F(n) / F(n+1) |
| 1 | 1 | 1 | 1.000000 |
| 2 | 1 | 2 | 0.500000 |
| 3 | 2 | 3 | 0.666667 |
| 4 | 3 | 5 | 0.600000 |
| 5 | 5 | 8 | 0.625000 |
| 6 | 8 | 13 | 0.615385 |
| 7 | 13 | 21 | 0.619048 |
| 8 | 21 | 34 | 0.617647 |
| 9 | 34 | 55 | 0.618182 |
| 10 | 55 | 89 | 0.617978 |
| →∞ | F(n) | F(n+1) | ≈ 0.6180339887… |
Визуально эту закономерность можно представить в виде золотой спирали, которая строится на основе прямоугольников, длины сторон которых соответствуют числам Фибоначчи. Начав с квадрата со стороной 1, мы добавляем к нему квадрат такого же размера, получая прямоугольник 2×1. Затем добавляем квадрат со стороной 2, получая фигуру 3×2, и так далее. Соединив дугами противоположные углы каждого квадрата, мы получаем спираль, которая по мере роста всё больше приближается к идеальной логарифмической спирали, построенной на основе золотого сечения.
Это свойство чисел fibonacci не просто математический курьез — оно стало основой для многочисленных приложений в архитектуре, дизайне и других областях, где гармоничные пропорции играют важную роль. Именно поэтому последовательность fibonacci и золотое сечение часто рассматриваются как математический фундамент эстетики.
Примеры чисел Фибоначчи в природе и искусстве
Удивительно, но последовательность fibonacci и связанное с ней золотое сечение проявляются во множестве природных форм и художественных произведений. Это наводит на мысль, что перед нами не просто математическая абстракция, а нечто большее — возможно, один из фундаментальных принципов организации материи и эстетического восприятия.
В растениях и живых организмах
Природа, кажется, особенно «любит» числа Фибоначчи, используя их в самых разных контекстах:
- Спирали подсолнечника — семена в корзинке подсолнуха формируют две системы спиралей: против часовой стрелки (обычно 21 спираль) и по часовой (34 спирали). Эти числа, как нетрудно заметить, являются соседними числами fibonacci.
- Расположение листьев на стебле (филлотаксис) — многие растения размещают листья так, чтобы максимизировать поступление солнечного света и воды. Угол расположения часто составляет около 137,5 градусов, что математически связано с золотым сечением.
- Соцветия и шишки — количество спиралей в ананасах, сосновых шишках и других подобных структурах почти всегда соответствует числам Фибоначчи (5, 8, 13).
- Раковины моллюсков — многие раковины, например наутилуса, растут по спирали, пропорции которой приближаются к золотому сечению. С каждым новым витком раковина увеличивается в размерах приблизительно в 1,618 раз.
- Ветвление растений — если подсчитать количество стеблей на каждом уровне ветвления некоторых растений, то получится последовательность fibonacci: 1, 1, 2, 3, 5, 8…
Эти закономерности не случайны — они возникают из эволюционной оптимизации роста и развития организмов, где числа fibonacci обеспечивают наиболее эффективное использование пространства и ресурсов.
В архитектуре и искусстве
Человеческая культура также интуитивно или осознанно обращается к пропорциям, связанным с последовательностью Фибоначчи:
- Древнегреческая архитектура — Парфенон и другие античные храмы строились с использованием пропорций, близких к золотому сечению, что придавало им особую гармоничность.
- Искусство Возрождения — Леонардо да Винчи активно применял золотое сечение в своих работах. В «Витрувианском человеке» и «Джоконде» пропорции соответствуют этому принципу.
- Современная архитектура — Ле Корбюзье разработал систему пропорций «Модулор», основанную на золотом сечении и размерах человеческого тела.
- Музыка — некоторые музыкальные композиции структурированы в соответствии с числами fibonacci. Например, кульминация произведения может находиться в точке, соответствующей золотому сечению от общей длительности.
- Современный дизайн — от логотипов (включая Apple) до веб-интерфейсов, принципы Фибоначчи и золотого сечения остаются актуальными инструментами создания визуально привлекательных композиций.
Эта универсальность последовательности fibonacci в природе и искусстве заставляет задуматься — случайно ли это совпадение, или мы имеем дело с глубинным эстетическим принципом, который одновременно является и математически оптимальным решением многих практических задач?
Зачем программистам нужны числа Фибоначчи
В мире информационных технологий последовательность fibonacci занимает особое место. На первый взгляд может показаться странным, что алгоритм, созданный для моделирования популяции кроликов в XIII веке, стал одним из базовых примеров в современном программировании. Однако его математическая элегантность и прикладная ценность делают его незаменимым инструментом для разработчиков и компьютерных наук в целом.
Пример рекурсивной функции на Python
Числа Фибоначчи часто используются как классический пример для демонстрации рекурсивных алгоритмов. Рекурсия — это подход, при котором функция вызывает сама себя, что идеально подходит для решения задач, которые можно разбить на аналогичные подзадачи меньшего размера. Вот как выглядит типичная рекурсивная реализация на Python:
def fibonacci(n):
# Базовый случай: для первых двух чисел возвращаем известные значения
if n <= 0:
return 0
elif n == 1:
return 1
# Рекурсивный случай: вычисляем как сумму двух предыдущих чисел
else:
return fibonacci(n-1) + fibonacci(n-2)
# Пример использования
print(fibonacci(10)) # Выведет 55
Этот код элегантно отражает математическую формулу, но имеет существенный недостаток: он крайне неэффективен для больших значений n из-за экспоненциального роста вычислений. Поэтому данный пример часто используется для обучения оптимизации алгоритмов, демонстрируя такие техники, как мемоизация (кэширование промежуточных результатов) или динамическое программирование.
Где ещё применяется
Последовательность Фибоначчи имеет несколько важных применений в компьютерных науках:
- Генерация псевдослучайных чисел — метод fibonacci с запаздыванием используется для создания последовательностей чисел, имитирующих случайные, что критически важно в криптографии, моделировании и других областях.
- Фибоначчиевый поиск — алгоритм поиска в отсортированном массиве, который использует числа fibonacci для определения промежуточных точек проверки. В некоторых ситуациях он эффективнее классического бинарного поиска.
- Балансировка нагрузки — в распределенных системах используется для создания стратегий экспоненциального отступления при повторных запросах, что помогает избежать перегрузки системы.
- Структуры данных — фибоначчиевы кучи представляют собой сложную, но эффективную реализацию очереди с приоритетами, которая обеспечивает оптимальную производительность для определенных операций.
- Тестирование и обучение — задача вычисления чисел fibonacci частый гость на технических собеседованиях, поскольку позволяет оценить понимание кандидатом базовых алгоритмических концепций, рекурсии и оптимизации.
Примечательно, что последовательность fibonacci служит не только практическим инструментом, но и своеобразным мостом между теоретической математикой и прикладным программированием. Она демонстрирует, как абстрактные математические концепции могут находить неожиданное применение в современных технологиях, подчеркивая важность фундаментальных знаний для решения практических задач.
Фибоначчи в трейдинге: правда или миф?
Финансовые рынки, при всей своей кажущейся непредсказуемости, часто демонстрируют определённые паттерны и циклические явления. В попытках формализовать эти закономерности, трейдеры обратились к математике, и числа fibonacci заняли в их инструментарии особое место. Так ли эффективен этот инструмент на практике, или мы имеем дело с красивым математическим мифом, который лишь создаёт иллюзию предсказуемости в принципиально хаотичной среде?
Ключевая концепция в техническом анализе — «уровни Фибоначчи», основанные на отношениях между числами этой последовательности. Они используются для определения потенциальных точек разворота тренда или уровней поддержки и сопротивления.
| Уровень | Значение | Происхождение | Интерпретация в трейдинге |
|---|---|---|---|
| 0% | 0.000 | Начальная точка | Начало отсчёта движения цены |
| 23.6% | 0.236 | √5 — 2 | Слабый уровень коррекции |
| 38.2% | 0.382 | 1 — 0.618 (обратное золотому сечению) | Умеренный откат |
| 50% | 0.500 | Психологический уровень (не из чисел fibonacci) | Середина движения |
| 61.8% | 0.618 | Золотое сечение | Классический уровень коррекции |
| 78.6% | 0.786 | Квадратный корень из 0.618 | Глубокий откат |
| 100% | 1.000 | Конечная точка | Полный возврат к исходной цене |
Трейдеры используют эти уровни для:
- Определения целей по прибыли
- Установки защитных стоп-приказов
- Прогнозирования точек входа при коррекции на восходящем тренде
- Анализа возможных уровней отскока цены
Критический взгляд
Несмотря на популярность, эффективность уровней Фибоначчи в трейдинге остаётся дискуссионным вопросом. Критики указывают на следующие аспекты:
- Самоисполняющееся пророчество:
Если достаточное количество трейдеров верит в значимость уровней Фибоначчи и действует соответственно, эти уровни действительно могут работать — но только из-за коллективных действий участников рынка, а не из-за какой-то внутренней математической магии.
- Отсутствие научного обоснования:
Не существует строгих научных доказательств того, что финансовые рынки должны подчиняться закономерностям fibonacci. Многие академические исследования ставят под сомнение статистическую значимость таких паттернов.
- Ретроспективная подгонка:
Легко найти соответствие уровням fibonacci, анализируя исторические данные постфактум, но гораздо сложнее использовать их для достоверных прогнозов.
Тем не менее, многие профессиональные трейдеры продолжают включать уровни Фибоначчи в свой аналитический инструментарий, комбинируя их с другими методами технического анализа для принятия более обоснованных торговых решений.
Почему числа Фибоначчи не всегда работают (и это нормально)
Несмотря на кажущуюся универсальность последовательности fibonacci и золотого сечения, необходимо сохранять критический взгляд на их применение. Как профессионалы в области аналитики данных, мы должны отличать математически обоснованные закономерности от случайных совпадений или подгонки фактов под желаемые шаблоны.
Существует несколько причин, по которым числа fibonacci не являются универсальным ключом к пониманию мира:
- Избирательность наблюдений — человеческий мозг склонен замечать закономерности даже там, где их нет (феномен, известный как апофения). Мы легко находим числа Фибоначчи в природе, потому что активно их ищем, игнорируя многочисленные случаи, где эта последовательность отсутствует.
- Приблизительность совпадений — многие «соответствия» последовательности fibonacci в природе являются приблизительными. Например, лепестки цветов не всегда точно соответствуют числам Фибоначчи, но мы склонны замечать те случаи, которые ближе к ожидаемым значениям.
- Математическая неизбежность — некоторые закономерности могут возникать просто потому, что они являются оптимальным решением для определенных задач. Например, спиральное расположение семян подсолнечника — это эффективный способ упаковки, который математически приводит к числам, близким к последовательности fibonacci, но это результат оптимизации, а не следствие какого-то мистического закона.
- Культурные предубеждения — западная культура исторически отдает предпочтение определенным пропорциям, что влияет на наше восприятие красоты и гармонии. Это может создавать иллюзию универсальности золотого сечения, которая на самом деле культурно обусловлена.
Важно понимать, что признание ограниченности применения чисел fibonacci не уменьшает их математической и практической ценности. Напротив, это позволяет нам более точно определить области, где данная последовательность действительно имеет объяснительную или предсказательную силу, отделяя их от ситуаций, где совпадения могут быть случайными или натянутыми.
В конечном счете, ценность последовательности Фибоначчи в различных областях — от биологии до дизайна — определяется не ее предполагаемой универсальностью, а конкретными практическими результатами, которые мы получаем, применяя основанные на ней принципы в каждом конкретном случае.
Краткий вывод: зачем нам все эти Фибоначчи
Подводя итоги нашего исследования последовательности Фибоначчи, можно выделить несколько ключевых причин, по которым эта математическая концепция остается актуальной и важной для различных областей знания:
- Междисциплинарный мост — числа fibonacci создают уникальное пересечение между математикой, природой, искусством и технологиями, демонстрируя единство принципов, лежащих в основе самых разных явлений.
- Инструмент оптимизации — как в природе, так и в человеческой деятельности, пропорции, связанные с последовательностью Фибоначчи, часто представляют собой оптимальные решения для задач эффективного использования пространства и ресурсов.
- Основа для инноваций — от компьютерных алгоритмов до архитектурного проектирования, принципы fibonacci продолжают вдохновлять новые творческие и технические решения.
- Развитие критического мышления — изучение как возможностей, так и ограничений применения чисел Фибоначчи способствует формированию более глубокого аналитического подхода к оценке закономерностей в окружающем мире.
В эпоху информационных технологий и искусственного интеллекта последовательность, открытая средневековым математиком, продолжает демонстрировать удивительную жизнеспособность, находя новые области применения и адаптируясь к современным вызовам. Возможно, в этой способности соединять прошлое и будущее, природное и рукотворное, математическое и эстетическое и заключается непреходящая ценность чисел fibonacci для человеческого познания.

Как создать собственный шрифт: пошаговое руководство для дизайнеров
Если давно хотели понять, как сделать свой шрифт, но не знали, с чего начать, — здесь вы быстро разберётесь в базовых шагах. Что учитывать в эскизах, чем отличаются метрики, как проверить читаемость и не запутаться в инструментах? Разбираем просто и по делу.

Конкурентный анализ: что это, зачем нужен и как его проводить
Конкурентный анализ — это не про слежку, а про здравый смысл. Как он помогает находить слабые места в нише, повышать прибыль и не повторять чужие ошибки? В статье — примеры и советы.

Что выбрать: ITSM или ITIL? Ответ для бизнеса
ITSM и ITIL часто упоминаются вместе, но что это такое на самом деле? Узнайте, как эти концепции помогают улучшить IT-услуги и оптимизировать процессы

Шаблонные строки в JavaScript: что это, зачем нужны и как использовать
Шаблонные строки в JavaScript — мощный инструмент, который может здорово упростить жизнь. Но знаете ли вы, где они действительно полезны, а где — нет?