Что такое корреляция и как её правильно интерпретировать в анализе данных
В мире данных, где каждый день генерируются терабайты информации, мы постоянно сталкиваемся с необходимостью понимать взаимосвязи между различными показателями. Возьмем простой пример: чем выше рост человека, тем больше его вес — интуитивно понятная закономерность. Или другая ситуация: офисные работники замечают, что в дни, когда они выпивают больше кофе, их продуктивность возрастает. Подобные наблюдения наводят на мысль о наличии связи между переменными, и именно здесь на помощь приходит корреляция — статистический инструмент, позволяющий количественно оценить степень взаимосвязи между двумя или более факторами.

Однако здесь кроется одна из самых распространенных ловушек в анализе данных. Обнаружение корреляции между переменными ни в коем случае не означает наличие причинно-следственной связи между ними. Эта фундаментальная ошибка — принятие корреляции за причинность — приводит к неверным выводам не только в научных исследованиях, но и в бизнес-аналитике, маркетинге и даже в повседневной жизни. Именно поэтому понимание того, что такое корреляция и как правильно её интерпретировать, становится критически важным навыком для любого, кто работает с данными.
- Что такое корреляция простыми словами
- Где и зачем применяется корреляция
- Виды коэффициентов корреляции
- Как интерпретировать коэффициент корреляции
- Заключение
- Рекомендуем посмотреть курсы по системной аналитике
Что такое корреляция простыми словами
Корреляция (от латинского correlatio — «соотношение») представляет собой статистическую меру, которая показывает, насколько два или более показателя изменяются согласованно друг с другом. В сущности, корреляция отвечает на вопрос: если один показатель меняется, можем ли мы ожидать изменения другого, и если да, то в какую сторону?
Рассматривая типы корреляционных связей, мы выделяем несколько основных категорий:
Прямая корреляция (X↑ → Y↑) — когда увеличение одной переменной сопровождается увеличением другой. Классический пример: рост рекламного бюджета и увеличение продаж, или повышение температуры воздуха и рост потребления мороженого.
Обратная корреляция (X↑ → Y↓) — противоположная ситуация, когда рост одного показателя ведет к снижению другого. Например, увеличение цены товара обычно приводит к снижению спроса на него, или рост уровня образования населения коррелирует со снижением уровня преступности.
Отсутствие связи — когда изменения в одной переменной никак не влияют на другую. Цвет волос человека, вероятно, никак не связан с его предпочтениями в музыке.
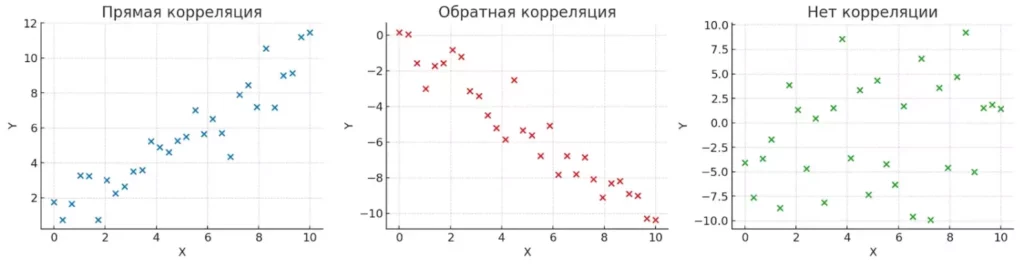
Три графика демонстрируют: слева — прямую связь, посередине — обратную, справа — отсутствие связи между переменными. Такие примеры позволяют быстро визуально понять различие между видами корреляции.
Однако природа корреляционных связей может быть различной.
Причинная связь предполагает, что одна переменная действительно влияет на другую.
Не причинная связь возникает, когда обе переменные зависят от третьего фактора — например, продажи солнцезащитных очков и купальников коррелируют не потому, что одно влияет на другое, а потому что оба зависят от сезона
Мнимая связь представляет собой статистический артефакт — случайное совпадение, которое не имеет реального объяснения и может исчезнуть при увеличении выборки или изменении временного периода.
Где и зачем применяется корреляция
Корреляционный анализ находит применение практически во всех сферах, где требуется работа с данными и выявление скрытых закономерностей. Рассмотрим основные области применения:
Аналитика данных — корреляция служит фундаментальным инструментом для Data Scientists и аналитиков при исследовании датасетов (выявление связей между пользовательским поведением и конверсией в e-commerce).
Маркетинг — специалисты используют корреляционный анализ для оптимизации рекламных кампаний (связь между временем показа рекламы и кликабельностью) и сегментации аудитории.
Социальные науки — исследователи применяют корреляцию для изучения общественных явлений (взаимосвязь между уровнем доходов и политическими предпочтениями).
Журналистика — корреляционный анализ помогает журналистам-расследователям выявлять неочевидные связи в данных (зависимость между государственными закупками и аффилированностью поставщиков).
Экономика — экономисты исследуют корреляции между макроэкономическими показателями (связь между уровнем безработицы и инфляцией).
Медицина — медицинские исследования часто базируются на корреляционном анализе (связь между образом жизни и заболеваемостью).
Важно понимать, что корреляция служит отправной точкой для более глубокого анализа. Она позволяет выдвигать гипотезы, которые затем требуют дополнительной проверки и изучения причинно-следственных механизмов.
Виды коэффициентов корреляции
Выбор подходящего коэффициента корреляции зависит от типа данных, характера распределения и целей исследования. Рассмотрим основные виды коэффициентов и области их применения.
Коэффициент Пирсона (r)
Коэффициент корреляции Пирсона является наиболее распространенным и широко используемым показателем линейной связи между двумя количественными переменными. Он применяется когда данные имеют нормальное распределение и между переменными предполагается линейная зависимость.
Когда применяется: для анализа числовых данных с нормальным распределением, при исследовании линейных зависимостей. Например, при изучении связи между ростом и весом людей, или между температурой процессора и его производительностью.
Основные характеристики: коэффициент принимает значения от -1 до +1, где значения близкие к +1 указывают на сильную положительную связь, близкие к -1 — на сильную отрицательную, а значения около 0 свидетельствуют об отсутствии линейной связи.
- Плюсы: простота интерпретации, высокая точность при линейных зависимостях, широкая применимость в различных областях науки.
- Минусы: чувствительность к выбросам (одно экстремальное значение может существенно исказить результат), неспособность выявлять нелинейные зависимости, требование нормального распределения данных.
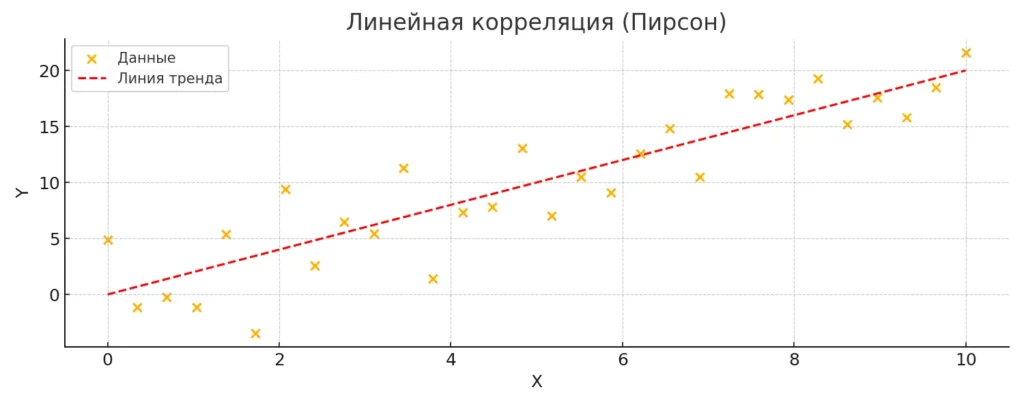
Этот график иллюстрирует линейную взаимосвязь между переменными — то, что измеряет коэффициент Пирсона. На диаграмме видно, что увеличение одной переменной сопровождается ростом другой.
Коэффициент Спирмена (ρ)
Ранговый коэффициент корреляции Спирмена предназначен для анализа связи между порядковыми переменными или количественными данными, которые не подчиняются нормальному распределению.
Область применения: идеально подходит для работы с рейтингами, опросами удовлетворенности, данными с выбросами. Например, при анализе связи между позицией в поисковой выдаче и количеством кликов, или между рейтингом сотрудника и размером премии.
Особенности: использует ранги значений вместо самих значений, что делает его устойчивым к выбросам и не требует предположений о распределении данных. Коэффициент Спирмена может выявлять монотонные зависимости (не обязательно линейные).
Коэффициент Кендалла (τ)
Коэффициент тау Кендалла также относится к ранговым корреляциям, но использует иной подход к расчету, основанный на подсчете согласованных и несогласованных пар наблюдений.
Отличие от Спирмена: коэффициент Кендалла более устойчив при работе с малыми выборками и лучше подходит для данных с большим количеством одинаковых рангов (связанных рангов). В машинном обучении его часто используют для оценки качества ранжирования алгоритмов.
Преимущества: более робастная оценка при наличии выбросов, лучшая производительность на малых выборках, интуитивная интерпретация через вероятность согласованности пар.
Коэффициент фи, Крамера, корреляционное отношение η
Для специфических типов данных существуют специализированные коэффициенты корреляции.
Коэффициент фи-корреляции применяется для анализа связи между двумя бинарными переменными. Например, при исследовании связи между наличием определенного симптома и положительным результатом медицинского теста.
Коэффициент Крамера V используется для номинальных переменных с более чем двумя категориями, основан на критерии хи-квадрат. Подходит для анализа связи между категориальными данными, такими как регион проживания и предпочитаемый бренд.
Корреляционное отношение η (эта) применяется для измерения нелинейной связи между переменными, когда одна переменная количественная, а другая — категориальная.
| Коэффициент | Тип данных | Шкала значений | Чувствительность к выбросам | Тип связи |
|---|---|---|---|---|
| Пирсона (r) | Количественные | -1 до +1 | Высокая | Линейная |
| Спирмена (ρ) | Порядковые/Количественные | -1 до +1 | Низкая | Монотонная |
| Кендалла (τ) | Порядковые | -1 до +1 | Очень низкая | Монотонная |
| Фи (φ) | Бинарные | -1 до +1 | Средняя | Линейная |
| Крамера (V) | Номинальные | 0 до +1 | Низкая | Любая |
Как интерпретировать коэффициент корреляции
Правильная интерпретация коэффициентов корреляции требует понимания не только численных значений, но и контекста исследования. Большинство коэффициентов корреляции варьируются в диапазоне от –1 до +1, где каждое значение несет определенную смысловую нагрузку.
Знак коэффициента указывает на направление связи: положительные значения свидетельствуют о прямой зависимости (когда одна переменная растет, другая тоже увеличивается), а отрицательные — об обратной (рост одной переменной сопровождается снижением другой). Абсолютное значение коэффициента отражает силу связи — чем ближе к единице, тем сильнее взаимосвязь между переменными.

Цветная шкала от -1 до +1 позволяет быстро оценить, насколько сильна и в каком направлении выражена корреляция. Такой визуальный инструмент облегчает интерпретацию значений в аналитике.
Для практического применения мы используем следующую общепринятую классификацию:
| Значение | Интерпретация |
|---|---|
| 0 | Отсутствие линейной связи |
| ±0.1–0.3 | Слабая связь |
| ±0.3–0.7 | Средняя (умеренная) связь |
| ±0.7–1.0 | Сильная связь |
Однако важно понимать, что эти границы являются условными и могут варьироваться в зависимости от области применения. В социальных науках корреляция 0.3 может считаться значимой, тогда как в физике или инженерии исследователи ожидают более высоких значений.
Особое внимание следует уделять интерпретации нулевой корреляции. Значение, близкое к нулю, означает отсутствие линейной связи, но не исключает наличие нелинейных зависимостей. Например, зависимость между углом поворота руля автомобиля и скоростью может показать нулевую корреляцию, хотя очевидно, что эти переменные связаны сложной нелинейной зависимостью.
При интерпретации результатов корреляционного анализа мы должны помнить о нескольких критически важных аспектах. Во-первых, статистическая значимость корреляции не всегда означает практическую значимость — при больших выборках даже очень слабые корреляции могут быть статистически значимыми. Во-вторых, контекст исследования имеет решающее значение: корреляция 0.2 между эффективностью нейросети и объемом обучающих данных может быть весьма важной для ML-инженеров, тогда как такая же корреляция между цветом упаковки и продажами продукта может не иметь практического значения.
Заключение
В эпоху больших данных и машинного обучения понимание корреляции становится не просто полезным навыком, а необходимым инструментом для принятия обоснованных решений. Мы рассмотрели, как корреляционный анализ помогает выявлять скрытые закономерности в данных — от простых примеров с ростом и весом до сложных зависимостей в поведении пользователей цифровых платформ. Корреляция показывает статистическую связь между переменными, но не всегда указывает на причину. Подведем итоги:
- Для разных данных существуют свои коэффициенты — Пирсона, Спирмена, Кендалла и другие. Каждый из этих коэффициентов подходит для определённых типов данных и задач, обеспечивая более точную оценку взаимосвязей.
- Интерпретировать значения важно с учётом сферы и особенностей данных. Без понимания контекста результаты могут быть неверно истолкованы, что приведёт к ошибочным выводам и решениям.
- Корреляционный анализ — основа для генерации гипотез, но не для окончательных выводов. Для подтверждения причинно-следственных связей необходимы дополнительные методы и эксперименты.
- Изучение корреляций помогает находить скрытые закономерности и повышать эффективность решений в бизнесе и науке. Это способствует улучшению предсказаний и оптимизации процессов, что ведёт к конкурентным преимуществам и научным открытиям.
Рекомендуем обратить внимание на подборку курсов по системной аналитике — отличный старт, если вы только начинаете осваивать профессию аналитика. В курсах есть теоретическая и практическая часть, чтобы вы смогли уверенно применять методы анализа на реальных задачах.
Рекомендуем посмотреть курсы по системной аналитике
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Аналитик данных
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
99 760 ₽
|
От
8 313 ₽/мес
Беспроцентная. На 1 год.
|
Длительность
6 месяцев
|
Старт
20 января
|
Ссылка на курсПодробнее |
|
Системный и бизнес-анализ в разработке ПО. Интенсив
|
Level UP
36 отзывов
|
Цена
75 000 ₽
|
От
18 750 ₽/мес
|
Длительность
1 месяц
|
Старт
23 января
|
Ссылка на курсПодробнее |
|
Системный аналитик PRO
|
Нетология
45 отзывов
|
Цена
с промокодом kursy-online
79 800 ₽
140 000 ₽
|
От
3 500 ₽/мес
Рассрочка на 2 года.
|
Длительность
10 месяцев
|
Старт
13 февраля
|
Ссылка на курсПодробнее |
|
Системный аналитик с нуля
|
Stepik
33 отзыва
|
Цена
4 500 ₽
|
|
Длительность
1 неделя
|
Старт
в любое время
|
Ссылка на курсПодробнее |
|
Системный аналитик с нуля до PRO
|
Eduson Academy
100 отзывов
|
Цена
Ещё -11% по промокоду
119 760 ₽
257 760 ₽
|
От
9 980 ₽/мес
10 740 ₽/мес
|
Длительность
6 месяцев
|
Старт
в любое время
|
Ссылка на курсПодробнее |

Горизонтальное управление: что это такое, принципы, преимущества и примеры внедрения
Горизонтальное управление — это попытка уйти от жёсткой иерархии и дать командам больше самостоятельности. Как такая модель влияет на скорость решений, мотивацию и результаты бизнеса? В этом материале разбираем принципы, риски и реальные сценарии внедрения.

Как рисовать в Illustrator и не сдаться на первых шагах
Работа в Adobe Illustrator кажется сложной? Разбираем основные инструменты, показываем пошаговый процесс создания векторных иллюстраций и раскрываем хитрости работы с программой.

Разработка под watchOS: как создавать приложения для Apple Watch с нуля
Что делать, если интерфейс не помещается, а батарея тает на глазах? Разработка под watchOS — это вызов. Но в этом гайде вы найдёте все нужные ответы.

Где искать работу в Москве, чтобы не тратить недели впустую?
В этом материале мы собрали лучшие сайты для поиска работы в Москве — с их плюсами, минусами и важными нюансами, о которых стоит знать заранее.