Что такое мемоизация и как она помогает в оптимизации алгоритмов
Мемоизация — это техника оптимизации, которая позволяет избежать повторных вычислений одних и тех же значений. Суть её проста: если функция уже была вызвана с определенными параметрами, мы сохраняем результат и при следующем обращении с теми же данными просто возвращаем его из кеша. Особенно эффективна в рекурсивных алгоритмах, где одна и та же подзадача может решаться десятки или даже тысячи раз.

Давайте разберемся, как это работает и почему мемоизация становится незаменимым инструментом при решении задач динамического программирования.
- Зачем нужна мемоизация
- Как работает мемоизация
- Реализация мемоизации на Python
- Сравнение мемоизации и bottom‑up
- Примеры: как решаются задачи с мемоизацией и без неё
- Плюсы и минусы мемоизации
- Когда не стоит использовать мемоизацию
- Рекомендуем посмотреть курсы по Python
Зачем нужна мемоизация
Представим типичную ситуацию: мы пишем рекурсивную функцию для решения задачи, которая естественным образом разбивается на подзадачи. Код выглядит элегантно, логика понятна, но при запуске программа работает невыносимо медленно. В чем причина? Чаще всего проблема кроется в том, что один и тот же фрагмент вычислений выполняется многократно.
Проблема избыточных вычислений в рекурсии (на примере Фибоначчи)
Классический пример — вычисление чисел Фибоначчи. Наивная рекурсивная реализация выглядит так:
def fib(n): if n <= 1: return n return fib(n-1) + fib(n-2)
При вызове fib(5) функция рекурсивно вычисляет fib(4) и fib(3). Но fib(4) в свою очередь снова вызывает fib(3) — и вот мы уже дважды считаем одно и то же значение. С ростом n количество повторных вычислений растет экспоненциально, достигая сложности O(2^n).
Когда простая реализация работает медленно
Проблема избыточных вычислений проявляется не только в числах Фибоначчи. Любая задача с перекрывающимися подзадачами — будь то поиск кратчайшего пути, подсчет числа способов разбиения или оптимизация ресурсов — сталкивается с тем же: рекурсия элегантна, но неэффективна без кеширования.
Как мемоизация экономит ресурсы
Мемоизация решает эту проблему радикально: каждый результат вычисляется ровно один раз и сохраняется в специальном хранилище (обычно словаре или массиве). При повторном обращении функция не пересчитывает значение, а просто возвращает его из кеша. Это снижает временную сложность до O(n) для того же алгоритма Фибоначчи — разница между секундами и миллисекундами при больших значениях n.
Как работает мемоизация
Механизм мемоизации можно описать тремя простыми шагами: проверка наличия результата в кеше, выполнение вычислений при необходимости и сохранение полученного значения для будущего использования. Давайте разберем каждый этап подробнее.
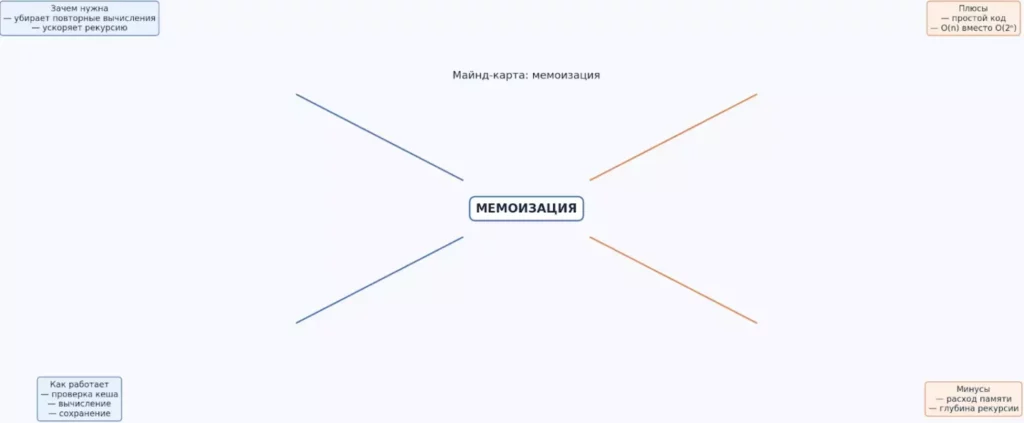
Майнд-карта суммирует ключевые идеи мемоизации: зачем она нужна, как работает и какие имеет плюсы и минусы. Такой обзор помогает быстро связать теорию с практикой перед разбором кода. Особенно полезна для первичного понимания техники оптимизации.
Словарь/объект как хранилище
В качестве кеша обычно используется словарь (в Python — dict), где ключом служит набор параметров функции, а значением — результат её выполнения. Например, для функции fib(n) ключом будет число n, а значением — соответствующее число Фибоначчи. Словарь удобен тем, что обеспечивает быстрый доступ к данным за O(1) в среднем случае.
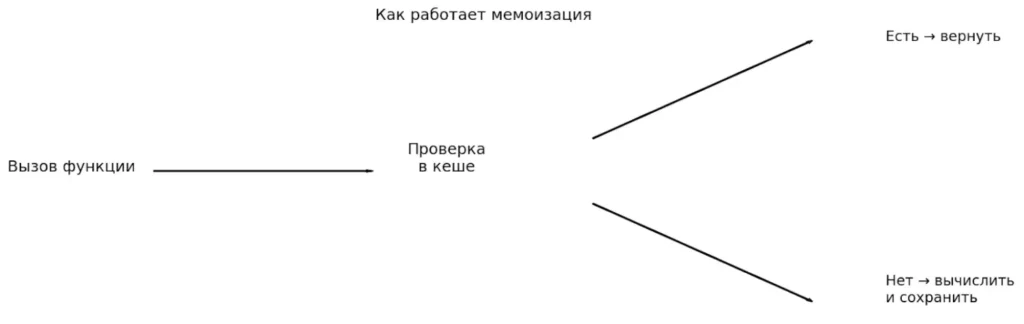
Схема иллюстрирует базовый алгоритм мемоизации: проверку наличия значения в кеше, вычисление при необходимости и сохранение результата. Такой подход гарантирует, что каждое значение вычисляется только один раз. Все последующие обращения получают результат мгновенно.
Условие проверки «есть ли значение в кеше»
Перед каждым вычислением функция проверяет: есть ли уже результат для данных параметров в кеше? Если да — возвращаем сохраненное значение и завершаем работу. Если нет — переходим к выполнению основной логики. Эта проверка добавляет минимальные накладные расходы, но экономит огромное количество времени на повторных вычислениях.
Когда и как происходит сохранение
Сохранение результата происходит сразу после завершения вычислений, перед возвратом значения. Псевдокод выглядит так:
если n в кеше: вернуть кеш[n] иначе: результат = вычислить(n) кеш[n] = результат вернуть результат
Таким образом, каждое новое вычисление автоматически пополняет кеш, и при последующих вызовах с теми же параметрами функция работает мгновенно.
Реализация мемоизации на Python
Теория — это хорошо, но давайте посмотрим, как мемоизация выглядит в реальном коде. Python предлагает несколько способов её реализации: от ручного управления кешем до использования встроенных декораторов.
Рекурсивная реализация с ручным кешем (memo = {})
Самый прямолинейный способ — создать словарь для хранения результатов и явно проверять его перед каждым вычислением:
def fib(n, memo=None):
if memo is None:
memo = {}
# далее логика...
Здесь мы передаем словарь memo как параметр (хотя можно объявить его и глобально). Перед рекурсивным вызовом проверяем наличие значения в кеше, а после вычисления сохраняем результат. Такой подход дает полный контроль над процессом кеширования.
Использование декоратора @lru_cache из functools
Python предлагает более элегантное решение — декоратор lru_cache, который автоматически кеширует результаты функции:
from functools import lru_cache @lru_cache(maxsize=None) def fib(n): if n <= 1: return n return fib(n-1) + fib(n-2)
Одна строка — и мемоизация готова. Параметр maxsize=None означает неограниченный размер кеша. Если указать конкретное число, декоратор будет хранить только последние N результатов (LRU — Least Recently Used).
Иллюстрация показывает разработчика, использующего мемоизацию в Python с помощью декоратора @lru_cache. Визуально подчёркивается идея повторного использования уже вычисленных результатов вместо повторных расчётов. Такой подход делает рекурсивный код проще и значительно быстрее без усложнения логики.
Сравнение двух способов (ручной vs встроенный)
| Критерий | Ручная мемоизация | @lru_cache |
| Простота кода | Требует явного управления словарем | Одна строка декоратора |
| Гибкость | Полный контроль над кешем | Ограничена возможностями декоратора |
| Производительность | Зависит от реализации | Оптимизирована на уровне C |
| Отладка | Легко увидеть содержимое кеша | Кеш скрыт внутри декоратора |
Для большинства задач декоратор удобнее, но если нужна тонкая настройка (например, очистка кеша по условию), ручной подход дает больше возможностей.
Сравнение мемоизации и bottom‑up
Мемоизация — не единственный способ избежать избыточных вычислений в динамическом программировании. Существует альтернативный подход, известный как bottom-up или табуляция. Давайте разберемся, чем они отличаются и когда стоит выбирать каждый из них.
Что такое bottom-up подход
Bottom-up — это итеративный метод решения задачи, при котором мы начинаем с базовых случаев и последовательно вычисляем все промежуточные значения до конечного результата. Для чисел Фибоначчи это выглядит так:
def fib_bottom_up(n): if n <= 1: return n dp = [0] * (n + 1) dp[1] = 1 for i in range(2, n + 1): dp[i] = dp[i-1] + dp[i-2] return dp[n]
Здесь мы заполняем массив dp от начала к концу, используя уже вычисленные значения. Никакой рекурсии — только последовательный цикл.
Чем отличается от мемоизации (top-down)
Мемоизация следует принципу top-down: мы начинаем с конечной задачи и рекурсивно разбиваем её на подзадачи, кешируя результаты по мере необходимости. Bottom-up работает в обратном направлении — от простейших случаев к сложным. Ключевое различие: мемоизация использует рекурсию и стек вызовов, bottom-up — итерацию и массив.
Когда какой способ выбрать
Выбор зависит от специфики задачи и ваших приоритетов. Мемоизация интуитивнее, когда рекурсивное решение очевидно — вы просто добавляете кеширование к естественной формулировке задачи. Bottom-up эффективнее по памяти (не нужен стек вызовов) и часто быстрее, но требует заранее понять порядок заполнения таблицы.
| Критерий | Мемоизация (top-down) | Bottom-up |
| Подход | Рекурсия + кеширование | Итерация + таблица |
| Сложность реализации | Проще для рекурсивных задач | Требует продумать порядок заполнения |
| Использование стека | Да, может быть проблемой при больших n | Нет, только массив |
| Скорость | Медленнее из-за вызовов функций | Быстрее за счет итераций |
| Решение подзадач | Только необходимые | Все подзадачи от базовых до конечной |
| Читаемость | Ближе к математическому определению | Более императивный стиль |
Если глубина рекурсии не критична и задача естественно формулируется рекурсивно — мемоизация удобнее. Если важна максимальная производительность и все подзадачи всё равно нужно решить — bottom-up предпочтительнее.
Примеры: как решаются задачи с мемоизацией и без неё
Теория становится понятнее на конкретных примерах. Давайте рассмотрим классическую задачу вычисления чисел Фибоначчи тремя способами и сравним их производительность.
Наивный перебор
Начнем с простейшей рекурсивной реализации без оптимизаций:
def fib_naive(n): if n <= 1: return n return fib_naive(n-1) + fib_naive(n-2)
Код максимально простой и понятный, но катастрофически медленный. При n = 40 функция выполнит более миллиарда вызовов. Временная сложность O(2^n) делает этот подход непригодным для любых практических задач с n > 30.
Мемоизация
Добавим кеширование результатов:
from functools import lru_cache @lru_cache(maxsize=None) def fib_memo(n): if n <= 1: return n return fib_memo(n-1) + fib_memo(n-2)
Одна строка декоратора — и сложность падает до O(n). Теперь fib_memo(100) выполняется мгновенно, тогда как наивная версия не справится и за часы. Каждое значение вычисляется ровно один раз, остальные обращения работают с кешем.
Bottom-up
Итеративный подход без рекурсии:
def fib_bottom_up(n): if n <= 1: return n prev, curr = 0, 1 for _ in range(2, n + 1): prev, curr = curr, prev + curr return curr
Этот вариант также работает за O(n), но использует всего O(1) дополнительной памяти (если не считать входное значение). Отсутствие рекурсии означает отсутствие риска переполнения стека — можно вычислить fib(10000) без проблем.
Сравнение по времени работы:
Для n = 35:
- Наивный перебор: ~5–10 секунд.
- Мемоизация: <0.001 секунды.
- Bottom-up: <0.001 секунды.
Для n = 100:
- Наивный перебор: практически бесконечно.
- Мемоизация: <0.001 секунды.
- Bottom-up: <0.001 секунды.
Разница очевидна: мемоизация и bottom-up на порядки эффективнее наивной рекурсии. Выбор между ними зависит от того, что важнее — простота кода (мемоизация) или максимальная производительность и экономия памяти (bottom-up).
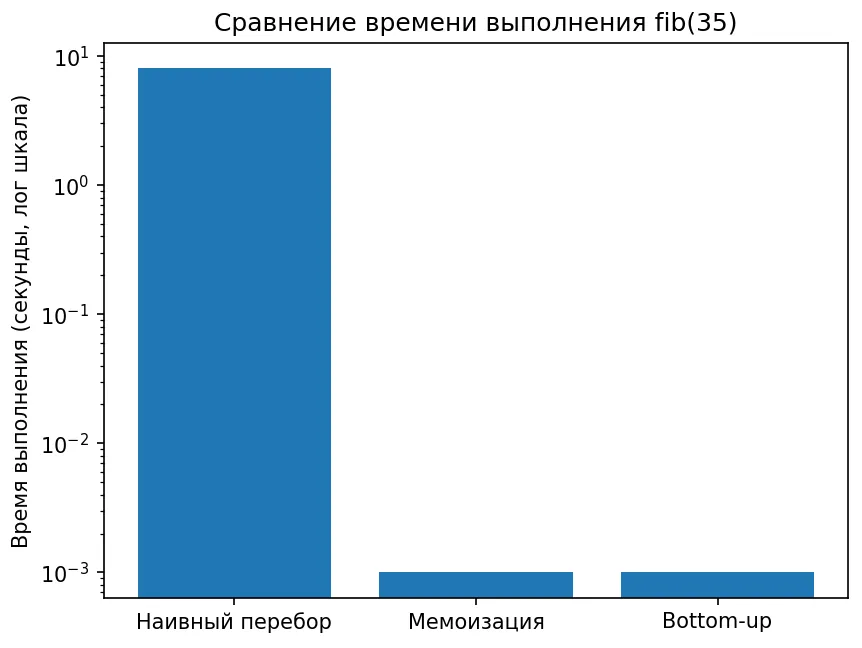
Сравнение времени выполнения алгоритмов вычисления чисел Фибоначчи для одного и того же значения n. Наивная рекурсия работает на порядки медленнее, тогда как мемоизация и bottom-up показывают сопоставимую высокую производительность. Логарифмическая шкала подчёркивает масштаб различий.
Плюсы и минусы мемоизации
Как и любая техника оптимизации, мемоизация имеет свои сильные и слабые стороны. Давайте систематизируем их, чтобы понимать, в каких ситуациях она действительно полезна, а где может создать дополнительные проблемы.
Преимущества:
- Простота внедрения — часто достаточно добавить декоратор или несколько строк для управления кешем, и рекурсивный код начинает работать в разы быстрее.
- Естественность решения — сохраняется рекурсивная структура, которая часто ближе к математическому определению задачи.
- Решение только необходимых подзадач — если для получения результата не требуется вычислять все промежуточные значения, мемоизация автоматически пропустит ненужные вычисления.
- Гибкость — можно легко добавить или убрать кеширование, не переписывая всю логику функции.
- Отладка — рекурсивный код часто проще отслеживать и понимать, чем сложные циклы с индексами.
Ограничения и недостатки:
- Потребление памяти — кеш может разрастись до значительных размеров, особенно если функция вызывается с большим количеством уникальных параметров.
- Использование стека вызовов — глубокая рекурсия может привести к переполнению стека (stack overflow), что ограничивает применимость на больших данных.
- Накладные расходы — каждый вызов функции создает новый фрейм в стеке, что медленнее итеративного подхода даже с кешированием.
- Сложность с изменяемыми параметрами — если функция принимает списки или словари, их нельзя напрямую использовать как ключи кеша без дополнительных преобразований.
- Не всегда оптимальна — для задач, где всё равно нужно вычислить все подзадачи, итеративный bottom-up обычно работает быстрее.
Ключевой момент: мемоизация — это компромисс между простотой реализации и эффективностью. Вы экономите время разработки и получаете понятный код, но платите дополнительной памятью и потенциальными проблемами со стеком. Для большинства практических задач этот компромисс оправдан.
Когда не стоит использовать мемоизацию
Мемоизация — мощный инструмент, но не универсальное решение. Существуют ситуации, когда её применение либо неэффективно, либо вовсе невозможно. Давайте рассмотрим основные сценарии, где от мемоизации лучше отказаться.
Слишком много параметров → взрыв кеша
Представьте функцию, которая принимает 5–6 параметров, каждый из которых может принимать десятки различных значений. Количество уникальных комбинаций растет экспоненциально, и кеш быстро съедает всю доступную память. Например, функция calculate(a, b, c, d, e), где каждый параметр варьируется от 0 до 100, теоретически может создать 100^5 = 10 миллиардов записей в кеше. На практике это приведет к исчерпанию памяти задолго до завершения вычислений.
Вывод: если пространство состояний слишком велико, мемоизация становится контрпродуктивной.
Побочные эффекты
Мемоизация работает только с чистыми функциями — теми, которые при одинаковых входных данных всегда возвращают одинаковый результат и не имеют побочных эффектов. Если функция читает файлы, обращается к базе данных, генерирует случайные числа или изменяет глобальное состояние, кеширование приведет к некорректному поведению.
import random @lru_cache def get_random_value(n): return random.randint(0, n) # Всегда вернет одно и то же!
Вывод: мемоизация несовместима с побочными эффектами и недетерминированными вычислениями.
Неоптимально при линейных задачах
Если задача решается простым циклом за O(n) без рекурсии, добавление мемоизации не даст никакого выигрыша, а только усложнит код и добавит накладные расходы. Например, простое суммирование элементов массива не требует кеширования — итерация справится эффективнее.
Вывод: мемоизация полезна только там, где есть перекрывающиеся подзадачи. Для линейных алгоритмов она избыточна.
Заключение
Мемоизация — это элегантный способ превратить медленный рекурсивный алгоритм в эффективное решение, добавив всего несколько строк кода. Мы рассмотрели, как она работает, когда применима и в чём её ограничения. Ключевой вывод прост: если ваша задача имеет перекрывающиеся подзадачи и естественным образом формулируется рекурсивно, мемоизация — отличный выбор для быстрой оптимизации. Подведем итоги:
- Мемоизация — это техника оптимизации рекурсивных алгоритмов. Она позволяет избежать повторных вычислений за счёт кеширования уже полученных результатов.
- Основная польза мемоизации — резкое снижение временной сложности. На примере чисел Фибоначчи она превращает экспоненциальный алгоритм в линейный.
- Мемоизация особенно эффективна для задач с перекрывающимися подзадачами. В таких сценариях кеширование даёт максимальный выигрыш по скорости.
- В Python ее можно реализовать вручную или с помощью декоратора @lru_cache. Встроенный подход упрощает код и снижает вероятность ошибок.
- Мемоизация имеет ограничения. Она потребляет дополнительную память и не подходит для функций с побочными эффектами или слишком большим пространством состояний.
Если вы только начинаете осваивать профессию программиста, рекомендуем обратить внимание на подборку курсов по Python. В таких программах есть и теоретическая база по алгоритмам, и практическая часть с реальными задачами. Это помогает быстрее понять, где и как применять мемоизацию на практике.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
5 февраля
|
Подробнее |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 марта
|
Подробнее |
|
Fullstack-разработчик на Python
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
175 800 ₽
308 367 ₽
|
От
5 139 ₽/мес
|
Длительность
18 месяцев
|
Старт
12 февраля
|
Подробнее |
|
Python-разработчик
|
Академия Синергия
35 отзывов
|
Цена
с промокодом KURSHUB
91 560 ₽
228 900 ₽
|
От
3 742 ₽/мес
0% на 24 месяца
|
Длительность
6 месяцев
|
Старт
3 февраля
|
Подробнее |
|
Профессия Python-разработчик
|
Skillbox
219 отзывов
|
Цена
Ещё -27% по промокоду
157 107 ₽
285 648 ₽
|
От
4 621 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
3 февраля
|
Подробнее |

Будущее промышленного дизайна: главные тренды 2025 года
Промышленный дизайн уже не просто про эстетику — технологии, экология и новые подходы меняют его правила. Какие тренды будут определять 2025 год?

Какой графический редактор выбрать вместо Photoshop
Не хотите платить за подписку Adobe? Узнайте, какие аналоги фотошопа могут заменить его без потери функциональности.

Как избежать SQL-инъекций в PHP? Практические советы и примеры
SQL-инъекции — одна из самых опасных угроз для PHP-приложений. Узнайте, как злоумышленники используют уязвимости в коде и как защитить свою базу данных с помощью безопасных методов программирования.

Что такое метод математической индукции и как он работает
Метод математической индукции — это не абстрактная теория, а практический инструмент, который помогает доказывать алгоритмы, проверять гипотезы и строить надёжные модели. В статье — всё, что нужно знать о его применении.