Что такое прогнозирование временных рядов и как его использовать

В мире, где данные становятся новой валютой, умение заглядывать в будущее превращается из магии в науку. Прогнозирование временных рядов — это именно тот инструмент, который позволяет нам превратить исторические данные в надежные предсказания о том, что произойдет завтра, на следующей неделе или через год.

Представьте себе ситуацию: вы управляете интернет-магазином и хотите понять, сколько товаров заказать на новогодние праздники. Или вы финансовый аналитик, пытающийся предсказать движение курса валют. А может быть, вы data scientist в крупной IT-компании, задача которого — спрогнозировать нагрузку на серверы в пиковые часы. Во всех этих случаях мы имеем дело с временными рядами — последовательностями данных, привязанных к определенным моментам времени.

Где применяется

Сегодня прогнозирование временных рядов находит применение в самых разнообразных сферах:

• Финансы и инвестиции — прогнозирование котировок акций, валютных курсов, процентных ставок.
• Ритейл и e-commerce — планирование запасов, прогноз спроса на товары, оптимизация логистики.
• Энергетика — прогнозирование потребления электроэнергии, планирование выработки.
• Маркетинг — предсказание эффективности рекламных кампаний, анализ сезонности продаж.
• IT и телекоммуникации — мониторинг нагрузки на серверы, прогнозирование трафика.
• Здравоохранение — эпидемиологические прогнозы, планирование ресурсов больниц.

Возникает закономерный вопрос: почему эта тема становится все более актуальной? Ответ кроется в растущих объемах данных и развитии аналитических технологий. То, что раньше требовало интуиции и опыта, теперь можно просчитать с помощью алгоритмов. Однако важно понимать — успешное прогнозирование требует не только знания методов, но и глубокого понимания природы данных, с которыми мы работаем.

Роль прогнозирования в принятии управленческих решений

Прогнозирование временных рядов стало незаменимым инструментом стратегического управления в современном бизнесе. В условиях высокой неопределенности и быстро меняющихся рыночных условий способность заглядывать в будущее на основе данных дает компаниям существенное конкурентное преимущество и позволяет принимать обоснованные решения вместо интуитивных догадок.

Грамотно построенные прогнозы помогают оптимизировать ключевые бизнес-процессы: от планирования закупок и управления запасами до распределения маркетингового бюджета и кадрового планирования. Компании, которые инвестируют в развитие аналитических компетенций, демонстрируют более стабильную финансовую performance и лучше адаптируются к изменениям внешней среды. Экономический эффект от внедрения систем прогнозирования часто измеряется миллионами долларов — за счет сокращения издержек, предотвращения потерь и выявления новых возможностей для роста.

Что такое временной ряд

Он представляет собой последовательность числовых значений, упорядоченных по времени и измеряемых через определенные интервалы. Звучит просто, но за этим определением скрывается мощный аналитический инструмент, который помогает нам понять закономерности в данных и делать обоснованные прогнозы.

Ключевая особенность заключается в зависимости от времени — каждое наблюдение привязано к конкретному моменту, и порядок этих наблюдений имеет критическое значение. В отличие от обычных статистических данных, где мы можем перемешать значения без потери смысла, во временных рядах последовательность sacred — нарушение порядка лишает данные их прогностической силы.

Рассмотрим, где мы встречаем ВР в повседневной жизни и бизнесе:

Финансовые рынки:

• Котировки акций Apple, Google или любой другой публичной компании.
• Курсы валют — от классических USD/EUR до криптовалют.
• Индексы фондовых бирж — S&P 500, NASDAQ, РТС.
• Цены на сырьевые товары — нефть, золото, пшеница.

Бизнес-метрики:

• Ежедневные продажи интернет-магазина.
• Количество посетителей веб-сайта по часам.
• Выручка компании по месяцам или кварталам.
• Конверсия рекламных кампаний в динамике.

Операционные данные:

• Температура в дата-центре каждую минуту.
• Нагрузка на серверы в течение суток.
• Потребление электроэнергии промышленным предприятием.
• Трафик на автомагистралях в разное время дня.

Социальные и экономические показатели:

• Уровень безработицы по регионам.
• Динамика населения городов.
• Рейтинги популярности в социальных сетях.
• Объемы поисковых запросов в Google Trends.

Что делает анализ временных рядов особенно интересным — так это наличие скрытых паттернов и взаимосвязей. Например, продажи мороженого демонстрируют четкую сезонность, связанную с температурой воздуха. Трафик корпоративных сайтов показывает регулярные спады в выходные дни. А котировки акций могут реагировать на новости с определенной задержкой.

ВР также характеризуются автокорреляцией — явлением, когда текущие значения статистически связаны с предыдущими. Это свойство становится основой для большинства методов прогнозирования: если мы понимаем, как прошлое влияет на настоящее, мы можем экстраполировать эти закономерности в будущее.

Компоненты временного ряда

Любой из них можно представить как композицию нескольких базовых компонентов, каждый из которых отражает определенные закономерности в данных. Понимание этих составляющих — ключ к успешному анализу и прогнозированию. Давайте разберемся, из чего складывается «анатомия» временного ряда.

Тренд представляет собой долгосрочную направленность изменений в данных. Это своего рода «генеральная линия» развития показателя во времени. Тренд может быть возрастающим (продажи смартфонов в период с 2007 по 2015 год), убывающим (тиражи печатных газет за последние два десятилетия) или практически горизонтальным (средняя температура в конкретном регионе за короткий период). В современном мире технологий мы часто наблюдаем экспоненциальные тренды — например, рост вычислительных мощностей или объемов данных, генерируемых социальными сетями.

Сезонность отражает регулярно повторяющиеся колебания, связанные с календарными циклами. Классический пример — всплеск продаж в предновогодний период или спад активности пользователей социальных сетей в августе (когда многие находятся в отпуске). Сезонность может проявляться на разных временных масштабах: внутри суток (пиковая нагрузка на транспорт в часы пик), недельные циклы (снижение активности в выходные), месячные или годовые паттерны. Особенно интересно анализировать сезонность в контексте цифровых продуктов — например, как меняется использование образовательных приложений в зависимости от учебного календаря.

Цикличность описывает более долгосрочные колебания, которые не привязаны к конкретным календарным периодам. В отличие от сезонности, циклы имеют переменную продолжительность и обычно связаны с экономическими, социальными или технологическими процессами. Яркий пример — экономические циклы рецессии и роста, которые могут длиться от двух до десяти лет. В IT-сфере мы наблюдаем технологические циклы — периоды бурного развития определенных направлений (как сейчас происходит с искусственным интеллектом), за которыми следуют периоды консолидации и стабилизации.

Случайные колебания (шум) представляют собой непредсказуемые флуктуации, которые нельзя объяснить трендом, сезонностью или цикличностью. Это может быть воздействие внешних факторов, ошибки измерений или просто случайная вариабельность процесса. Примером может служить внезапный всплеск продаж из-за вирусного поста в социальных сетях или провал в трафике веб-сайта из-за технического сбоя.

Декомпозиция временного ряда — это процесс выделения и анализа каждой из описанных компонент. Существует два основных подхода к декомпозиции: аддитивная модель (когда компоненты суммируются) и мультипликативная (когда они перемножаются). Выбор модели зависит от характера данных: если амплитуда сезонных колебаний остается постоянной во времени, используется аддитивная модель; если амплитуда изменяется пропорционально уровню ряда — мультипликативная.

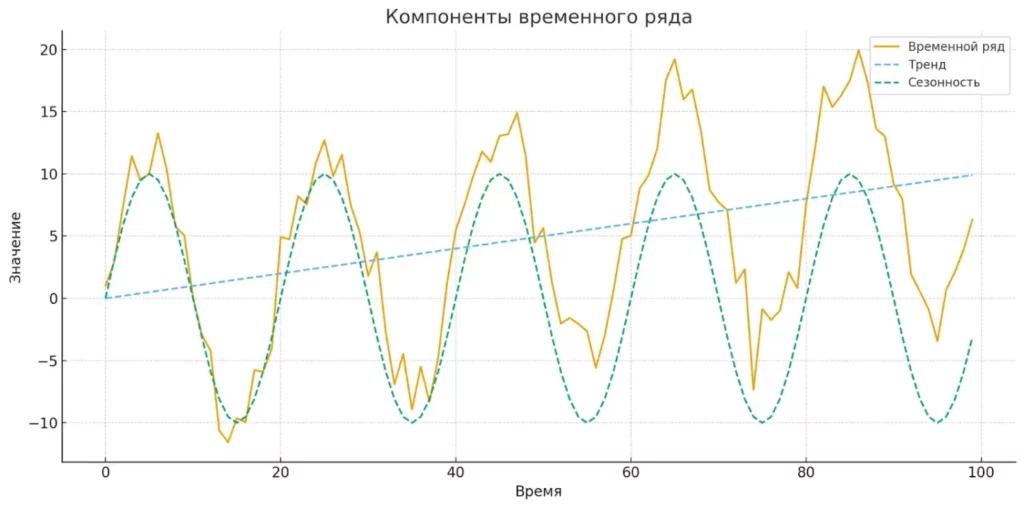
Диаграмма показывает, как складываются тренд, сезонность и шум, формируя общий временной ряд. Такая визуализация помогает понять, из каких частей состоит модель данных.

Процесс декомпозиции помогает аналитикам понять природу данных, выявить скрытые закономерности и выбрать наиболее подходящие методы прогнозирования. Например, если в данных доминирует тренд, имеет смысл использовать методы, специализирующиеся на экстраполяции долгосрочных тенденций. Если же преобладает сезонность, стоит обратить внимание на сезонные модификации классических алгоритмов.

Типы

Классификация временных рядов — это не просто академическое упражнение, а практическая необходимость для выбора правильных методов анализа. Понимание типа данных, с которыми мы работаем, определяет весь дальнейший подход к их обработке и прогнозированию.

Регулярные и нерегулярные

Регулярные ряды характеризуются постоянными интервалами между наблюдениями — данные собираются каждую секунду, минуту, час, день или в любом другом фиксированном ритме. Они удобны для анализа и являются «золотым стандартом» для большинства алгоритмов прогнозирования. Примеры: котировки акций (обновляются каждую секунду во время торговых сессий), метеорологические данные (измерения каждый час), ежедневная выручка интернет-магазина.

Нерегулярные собираются с переменными интервалами, что создает дополнительные сложности в анализе. Классический пример — транзакции в банке: клиенты совершают операции в произвольные моменты времени, и промежутки между транзакциями могут варьироваться от секунд до месяцев. Для работы с такими данными часто требуется предварительная агрегация — например, подсчет количества транзакций за день или суммирование объемов за неделю.

Детерминированные и недетерминированные

Детерминированные следуют строгим математическим закономерностям и полностью предсказуемы, если известна их структура. Представьте себе синусоидальную функцию времени — зная формулу, мы можем точно вычислить любое будущее значение. В реальном мире чисто детерминированные ряды встречаются редко, но некоторые процессы приближаются к этому идеалу — например, астрономические циклы или работа хорошо настроенного производственного оборудования.

Недетерминированные содержат случайную компоненту, что делает точное прогнозирование невозможным. Однако это не означает, что такие ряды непредсказуемы — мы можем прогнозировать их статистические характеристики (среднее значение, дисперсию, вероятностные распределения). Большинство реальных временных рядов относятся именно к этой категории: продажи, цены акций, погодные условия.

Стационарные и нестационарные

Стационарность — одно из ключевых понятий в анализе временных рядов, и понимание этого свойства критически важно для правильного выбора методов прогнозирования.

Стационарный характеризуется постоянными статистическими свойствами во времени: среднее значение, дисперсия и автокорреляционная функция не изменяются. Такие ряды «не помнят» о том, в какой момент времени мы их наблюдаем — их поведение одинаково в любой период. Примером может служить шум в электронных устройствах или флуктуации температуры в хорошо изолированном помещении с постоянным климат-контролем.

Нестационарные демонстрируют изменяющиеся во времени статистические характеристики. Это могут быть ряды с трендом (постоянно растущая выручка компании), изменяющейся дисперсией (волатильность финансовых инструментов в кризисные периоды) или эволюционирующими корреляционными связями. Большинство экономических и бизнес-показателей относятся к этой категории.

Проверка стационарности осуществляется с помощью специальных статистических тестов. Наиболее популярный — расширенный тест Дики-Фуллера (Augmented Dickey-Fuller test), который проверяет гипотезу о наличии единичного корня в ряду. Если p-значение теста меньше выбранного уровня значимости (обычно 0.05), мы можем отвергнуть нулевую гипотезу и считать ряд стационарным.

Почему стационарность так важна? Многие классические методы анализа временных рядов разработаны именно для стационарных данных. Применение этих методов к нестационарным рядам может привести к ложным корреляциям и неточным прогнозам. Поэтому нестационарные часто требуют предварительного преобразования для приведения их к стационарному виду — процесс, который мы рассмотрим в следующих разделах.

Подготовка данных к прогнозированию

Качество прогноза напрямую зависит от качества исходных данных — принцип «мусор на входе, мусор на выходе» особенно актуален для анализа временных рядов. Даже самые совершенные алгоритмы машинного обучения не смогут компенсировать серьезные проблемы в данных. Поэтому подготовка данных становится одним из самых важных этапов всего процесса.

1. Проверка полноты и качества данных.

Первым шагом всегда должна быть комплексная диагностика временного ряда. Мы проверяем наличие всех временных меток в ожидаемом диапазоне — отсутствующие наблюдения могут существенно исказить анализ сезонности и трендов. Особое внимание следует уделить регулярности интервалов: если данные должны собираться каждый час, но в ряду есть пропуски на несколько часов, это требует специального внимания.

Параллельно необходимо провести поиск аномальных значений. Аномалии могут быть результатом ошибок измерения, сбоев в системах сбора данных или действительно экстремальных событий. Классический пример — температура 150°C в метеорологических данных явно указывает на техническую ошибку, тогда как резкий всплеск продаж может быть связан с успешной маркетинговой акцией.

2. Заполнение пропусков.

Выбор метода заполнения пропусков зависит от природы данных и характера отсутствующих значений:

Заполнение константными значениями — используем среднее арифметическое или медиану для данных без выраженных трендов и сезонности. Медиана предпочтительнее при наличии выбросов, поскольку она более устойчива к экстремальным значениям.

Forward fill / Backward fill — заполнение предыдущими или последующими значениями эффективно для относительно стабильных процессов. Однако множественное повторение одного значения может исказить автокорреляционную структуру ряда.

Скользящее среднее — вычисляем среднее значение в окне вокруг пропущенного наблюдения. Этот подход хорошо работает для сглаживания локальных флуктуаций, но может «размывать» важные паттерны.

Интерполяция — линейная интерполяция предполагает равномерное изменение между соседними точками, что подходит для трендовых данных. Для более сложных зависимостей используются полиномиальная интерполяция или сплайны, которые могут учесть нелинейные изменения.

3. Обработка аномалий.

Стратегия работы с выбросами требует понимания их природы. Если аномалия связана с техническими ошибками, её следует исправить или удалить. Однако если выброс отражает реальное событие (например, пиковые продажи в «Черную пятницу»), его удаление может лишить модель важной информации о поведении системы в экстремальных условиях.

Для автоматического обнаружения аномалий используются различные подходы: статистические методы (правило трех сигм, межквартильный размах), алгоритмы изоляционного леса или методы, основанные на реконструкции данных с помощью автоэнкодеров.

4. Приведение к стационарности.

Большинство классических методов прогнозирования требуют стационарности данных. Если тест Дики-Фуллера показывает нестационарность, необходимо применить соответствующие преобразования. Процесс преобразования включает устранение тренда, сезонности и стабилизацию дисперсии.

Важно понимать, что подготовка данных — это итеративный процесс. После каждого преобразования необходимо повторно проверять качество данных и корректировать подход при необходимости. Хорошо подготовленный временной ряд должен быть стационарным, не содержать существенных пропусков и аномалий, а его статистические свойства должны быть стабильными во времени.

Стоит отметить, что в эпоху больших данных и реального времени подготовка данных часто должна происходить автоматически. Это создает дополнительные требования к робастности алгоритмов обработки и необходимости мониторинга качества данных в реальном времени.

Преобразования временных рядов

Когда мы сталкиваемся с нестационарным временным рядом, простого удаления аномалий и заполнения пропусков недостаточно. Необходимы специальные математические преобразования, которые помогут привести данные к виду, пригодному для анализа классическими методами. Рассмотрим основные техники, которые стали стандартом в арсенале современного аналитика.

Логарифмирование

Логарифмическое преобразование — один из самых простых и эффективных способов стабилизации дисперсии. Особенно полезно, когда размах колебаний пропорционален уровню ряда — ситуация, типичная для многих экономических показателей. Например, если выручка компании растет, то и абсолютные колебания продаж обычно увеличиваются, но относительные колебания могут оставаться стабильными.

Применяя натуральный логарифм ln(x), мы преобразуем мультипликативные отношения в аддитивные, что существенно упрощает анализ. Логарифмирование также имеет важное практическое преимущество: логарифмические приращения приближенно равны процентным изменениям, что делает результаты более интерпретируемыми для бизнеса.

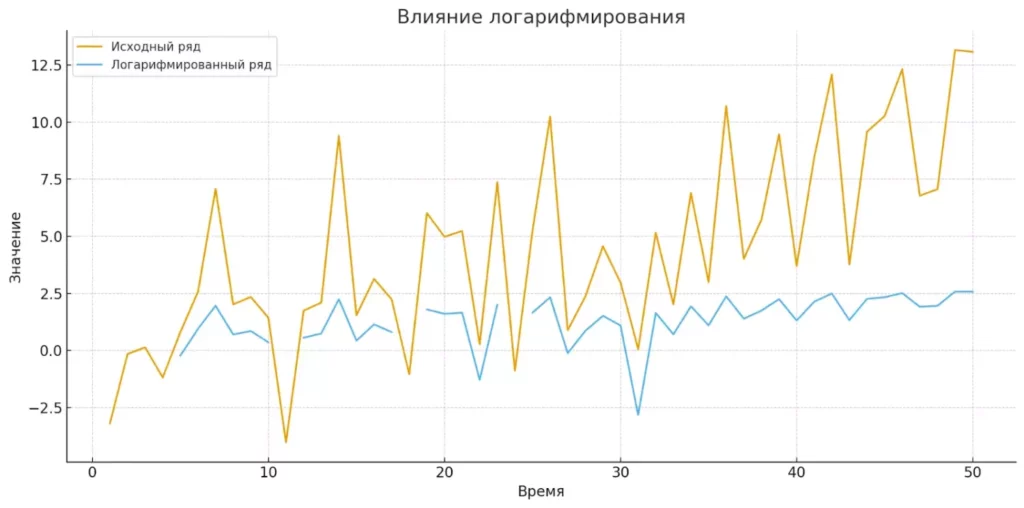
Сравнение исходного временного ряда и логарифмированного. Логарифмирование помогает уменьшить амплитуду колебаний и стабилизировать дисперсию данных.

Важное ограничение: логарифм определен только для положительных значений, поэтому данные должны быть строго больше нуля.

Преобразование Бокса-Кокса

Преобразование Бокса-Кокса представляет собой обобщение логарифмирования и позволяет найти оптимальную степенную трансформацию данных. Формула выглядит следующим образом:

y(λ) = (x^λ — 1) / λ при λ ≠ 0 y(λ) = ln(x) при λ = 0

Параметр λ (лямбда) определяет тип преобразования: при λ = 1 получаем исходные данные, при λ = 0.5 — извлечение квадратного корня, при λ = 0 — логарифмирование, при λ = -1 — обратную величину. Оптимальное значение λ обычно находится методом максимального правдоподобия.

Преобразование Бокса-Кокса особенно эффективно для данных с изменяющейся дисперсией и может значительно улучшить качество прогнозов. В современных библиотеках Python (scipy.stats) реализованы как прямое, так и обратное преобразования, что позволяет легко переводить прогнозы обратно в исходный масштаб.

Дифференцирование

Дифференцирование — основной инструмент для устранения трендов и приведения ряда к стационарности. Идея заключается в том, что вместо исходных значений мы анализируем их изменения (разности).

Обычное дифференцирование первого порядка вычисляется как:

Δx_t = x_t — x_{t-1}

Такое преобразование эффективно устраняет линейные тренды. Если тренд нелинейный, может потребоваться дифференцирование второго порядка:

Δ²x_t = Δx_t — Δx_{t-1} = x_t — 2x_{t-1} + x_{t-2}

Для данных с сезонностью применяется сезонное дифференцирование:

Δ_s x_t = x_t — x_{t-s}

где s — длина сезонного периода (12 для месячных данных с годовой сезонностью, 7 для дневных данных с недельной сезонностью).

В сложных случаях может потребоваться комбинирование различных типов дифференцирования. Например, для месячных данных с трендом и сезонностью сначала применяется сезонное дифференцирование (период 12), а затем обычное дифференцирование для устранения оставшегося тренда.

Важно не переусердствовать с дифференцированием: каждая операция уменьшает длину ряда и может привести к «передифференцированию», когда мы создаем ложную изменчивость в данных. Оптимальная степень дифференцирования определяется с помощью статистических тестов или информационных критериев.

Правильное применение этих преобразований требует понимания природы данных и задач анализа. В современной практике часто используются автоматизированные процедуры, которые подбирают оптимальные параметры преобразований на основе статистических критериев, но знание принципов остается необходимым для интерпретации результатов и контроля качества.

Математическая статистика как основа качественного прогнозирования

Перед погружением в конкретные методы прогнозирования важно понимать, что успешное применение любых моделей временных рядов требует твердых знаний основ математической статистики. Без понимания ключевых концепций — дисперсии, корреляции, p-значений, доверительных интервалов — аналитик рискует неправильно интерпретировать результаты и принять ошибочные решения.

Особенно критично понимание концепций статистической значимости и проверки гипотез. Многие методы, включая тесты на стационарность и выбор параметров ARIMA-моделей, основаны на статистических тестах, результаты которых необходимо корректно интерпретировать. Автокорреляционный анализ, лежащий в основе большинства классических подходов, также требует понимания статистической природы временных зависимостей.

Рекомендуется начинать изучение прогнозирования временных рядов с освежения знаний базовой статистики. Это инвестиция времени, которая многократно окупится более глубоким пониманием моделей и способностью критически оценивать качество получаемых прогнозов. Помните: статистическая грамотность — это не просто техническое требование, а основа для принятия взвешенных аналитических решений.

Методы прогнозирования

Арсенал методов прогнозирования временных рядов за последние десятилетия существенно расширился — от классических статистических подходов до современных решений на основе глубокого обучения. Выбор подходящего метода зависит от природы данных, горизонта прогнозирования и требований к точности и интерпретируемости результатов.

Статистические методы

Авторегрессия (AR). Модель авторегрессии основана на предположении, что текущее значение ряда можно выразить как линейную комбинацию его предыдущих значений. AR(p) модель имеет вид:

x_t = c + φ₁x_{t-1} + φ₂x_{t-2} + … + φₚx_{t-p} + ε_t

где p — порядок модели, φᵢ — параметры авторегрессии, ε_t — случайная ошибка.

Авторегрессионные модели хорошо работают с данными, где наблюдается сильная корреляция между соседними значениями. Классический пример — котировки акций, где цена сегодня сильно зависит от цены вчера. Порядок модели p обычно определяется с помощью информационных критериев (AIC, BIC) или анализа частной автокорреляционной функции.

Скользящее среднее (MA). Модель скользящего среднего представляет текущее значение как линейную комбинацию текущей и прошлых случайных ошибок:

x_t = μ + ε_t + θ₁ε_{t-1} + θ₂ε_{t-2} + … + θ_qε_{t-q}

где μ — константа, θᵢ — параметры скользящего среднего, q — порядок модели.

MA модели эффективны для данных, где влияние внешних шоков постепенно затухает. Порядок q определяется по автокорреляционной функции остатков.

ARIMA модели. ARIMA (AutoRegressive Integrated Moving Average) объединяет авторегрессию, интегрирование (дифференцирование) и скользящее среднее в единую модель ARIMA(p,d,q), где d — степень дифференцирования, необходимая для достижения стационарности.

ARIMA стала золотым стандартом для многих приложений благодаря своей гибкости и теоретической обоснованности. Модель способна описывать широкий спектр временных рядов и обеспечивает хорошую интерпретируемость результатов.

SARIMA модели. Seasonal ARIMA расширяет базовую ARIMA для учета сезонных паттернов. SARIMA(p,d,q)(P,D,Q)s включает дополнительные сезонные параметры, где s — длина сезонного периода, а P, D, Q — сезонные аналоги основных параметров.

SARIMA особенно эффективна для данных с четко выраженной сезонностью — например, продажи сезонных товаров, энергопотребление или туристические потоки.

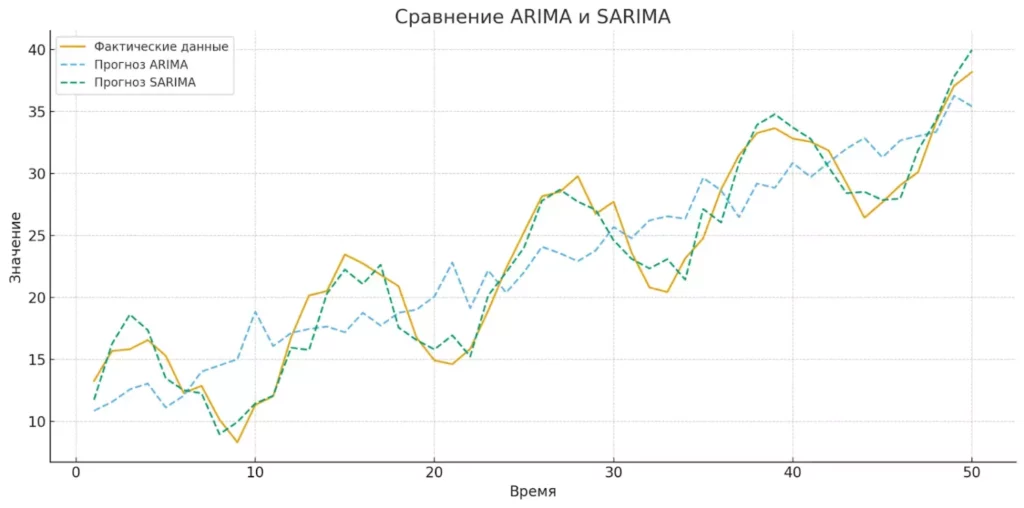
График показывает разницу между прогнозами моделей ARIMA и SARIMA. SARIMA лучше учитывает сезонные колебания, что делает её более точной для данных с повторяющимися паттернами.

Методы сглаживания

Простое экспоненциальное сглаживание. Экспоненциальное сглаживание основано на идее взвешенного усреднения, где более свежие наблюдения получают больший вес:

ŷ_{t+1} = αy_t + (1-α)ŷ_t

где α ∈ (0,1) — параметр сглаживания. При α близком к 1 модель быстро адаптируется к изменениям, при α близком к 0 — дает более консервативные прогнозы.

Модель Хольта-Винтерса. Метод Хольта-Винтерса расширяет экспоненциальное сглаживание для учета тренда и сезонности. Модель включает три компонента: уровень, тренд и сезонная составляющая, каждая из которых обновляется с помощью собственного параметра сглаживания.

Этот подход особенно популярен в бизнес-приложениях благодаря простоте реализации и интерпретации результатов.

Методы машинного обучения

Нейронные сети. Рекуррентные нейронные сети (RNN) и их усовершенствованные версии — LSTM (Long Short-Term Memory) и GRU (Gated Recurrent Units) — произвели революцию в прогнозировании временных рядов. LSTM особенно эффективны для работы с длинными последовательностями благодаря способности «помнить» важную информацию на больших временных интервалах.

Современные архитектуры, такие как Transformer и его модификации, показывают выдающиеся результаты в задачах прогнозирования, особенно для многомерных временных рядов.

Градиентный бустинг. Алгоритмы типа XGBoost, LightGBM и CatBoost адаптированы для работы с временными рядами через создание признаков, основанных на лагах, скользящих статистиках и календарных переменных. Эти методы особенно эффективны для данных с нелинейными зависимостями и взаимодействиями между различными факторами.

Специализированные решения. DeepAR, Prophet и N-BEATS представляют новое поколение методов, специально разработанных для временных рядов. Они сочетают преимущества глубокого обучения с пониманием специфики временных данных.

Prophet*, например, автоматически выделяет тренды, сезонность и праздничные эффекты, что делает его особенно удобным для бизнес-аналитиков без глубоких знаний в области машинного обучения.

*компания Meta признана экстремистской организацией, и ее деятельность запрещена в России.

Главная страница сервиса Prophet.

Выбор метода должен основываться на характеристиках данных, требованиях к точности, горизонте прогнозирования и доступных вычислительных ресурсах. Часто оптимальным решением становится ансамбль различных подходов, который объединяет сильные стороны разных методов.

Практические примеры применения

Теория приобретает смысл только в контексте реальных задач. Рассмотрим несколько практических сценариев, которые демонстрируют, как различные методы прогнозирования временных рядов применяются в современном бизнесе и науке.

Прогнозирование продаж интернет-магазина

Представим себе среднего размера e-commerce проект, специализирующийся на продаже электроники. Компания накопила три года ежедневных данных о продажах и хочет оптимизировать управление запасами, спрогнозировав спрос на следующий квартал.

Анализ данных выявляет несколько важных паттернов: четкую сезонность с пиками в предновогодний период и во время распродаж, недельную цикличность с провалами в выходные дни, и общий восходящий тренд. Присутствуют также аномальные всплески, связанные с вирусными публикациями в социальных сетях или акциями конкурентов.

Для такой задачи оптимальным решением становится комбинированный подход. SARIMA модель хорошо улавливает регулярные сезонные паттерны и базовый тренд. Дополнительно используется модель машинного обучения (например, LightGBM) с признаками, включающими информацию о маркетинговых кампаниях, праздничных днях, ценах конкурентов и внешних факторах (курс валют, индексы потребительского доверия). Финальный прогноз получается как взвешенная комбинация обеих моделей.

Результат: снижение издержек на складское хранение на 15% при одновременном сокращении случаев дефицита товаров на 25%. Особенно важно, что модель позволила заблаговременно подготовиться к сезонным пикам спроса.

Прогнозирование нагрузки на IT-инфраструктуру

Крупная технологическая компания сталкивается с необходимостью прогнозирования нагрузки на серверы для оптимального планирования ресурсов и предотвращения перегрузок. Данные собираются каждую минуту и включают метрики CPU, памяти, сетевого трафика и количества активных пользователей.

Специфика задачи заключается в наличии множественных временных масштабов: внутридневные циклы (пиковая активность в рабочие часы), недельные паттерны (снижение нагрузки в выходные), сезонные эффекты (рост активности в определенные периоды года) и непредсказуемые всплески из-за вирусного контента или технических проблем.

Здесь эффективным оказывается иерархический подход с использованием ансамбля моделей. На верхнем уровне LSTM сети анализируют долгосрочные тренды и сезонные паттерны. На среднем уровне модели типа Prophet обрабатывают недельные и дневные циклы. На нижнем уровне быстро адаптирующиеся модели экспоненциального сглаживания отслеживают краткосрочные флуктуации.

Критически важным становится режим реального времени: модели обновляются каждые несколько минут, и система автоматически масштабирует ресурсы на основе прогнозов. Результат: сокращение времени отклика приложений на 30% и экономия на инфраструктурных расходах до 20% за счет более эффективного использования ресурсов.

Анализ финансовых рынков

Hedge-фонд разрабатывает систему для прогнозирования волатильности валютных пар с целью оптимизации торговых стратегий. В отличие от предыдущих примеров, здесь приоритет отдается не точности точечных прогнозов, а правильной оценке рисков и неопределенности.

Финансовые временные ряды характеризуются кластеризацией волатильности (периоды высокой изменчивости следуют за периодами высокой изменчивости), толстыми хвостами распределений и нелинейными зависимостями. Классические методы часто оказываются недостаточными для учета этих особенностей.

Решение строится на основе GARCH семейства моделей для базового прогнозирования волатильности, дополненных ансамблем нейронных сетей, которые учитывают корреляции между различными активами, макроэкономические индикаторы и настроения рынка (анализ новостных потоков с помощью NLP). Особое внимание уделяется байесовским подходам, которые позволяют количественно оценить неопределенность прогнозов.

Ключевой особенностью стала интеграция альтернативных данных: спутниковые снимки для оценки экономической активности, анализ социальных сетей для определения настроений инвесторов, высокочастотные данные о торговых потоках.

Результат: повышение Sharpe ratio торговых стратегий на 40% и значительное снижение максимальных просадок в периоды рыночной турбулентности.

Энергетический сектор: прогнозирование потребления

Региональная энергетическая компания решает задачу прогнозирования электропотребления для оптимизации работы генерирующих мощностей и участия в энергетических торгах. Потребление электроэнергии демонстрирует сложную многомасштабную структуру: внутридневные пики, связанные с деловой активностью, недельные циклы, сезонные колебания и сильную зависимость от погодных условий.

Решение объединяет физические модели (учитывающие зависимость потребления от температуры, влажности, освещенности) со статистическими методами. Базовый прогноз строится с помощью SARIMA для регулярных компонент и дополняется моделями машинного обучения, которые учитывают нелинейные эффекты погодных условий, календарные особенности (праздники, школьные каникулы) и экономические факторы.

Результат: повышение точности краткосрочных прогнозов (на сутки вперед) до 97%, что позволило снизить затраты на балансирующую энергию на 12% и улучшить надежность энергоснабжения региона.

Эти примеры демонстрируют, что успешное применение прогнозирования временных рядов требует не только знания алгоритмов, но и глубокого понимания предметной области, творческого подхода к комбинированию различных методов и умения работать с неопределенностью и ограничениями реального мира.

Заключение

Прогнозирование временных рядов превратилось из узкоспециализированной статистической техники в фундаментальный инструмент современной аналитики данных. По мере того как цифровизация проникает во все сферы деятельности, умение извлекать инсайты из временных данных становится критически важным навыком для специалистов самых разных профилей. Подведем итоги:

• Прогнозирование временных рядов — это инструмент анализа данных. Он позволяет строить прогнозы на основе прошлых и текущих значений.
• Качество данных влияет на точность моделей. Подготовка, очистка и проверка временного ряда критически важны.
• Методы прогнозирования делятся на классические и современные. Используются ARIMA, SARIMA, Prophet и нейросети.
• Применение прогнозирования охватывает бизнес, науку, финансы и ИТ. Модели помогают принимать обоснованные решения.
• Глубокое понимание структуры ряда повышает точность. Анализ трендов, сезонности и шума улучшает результат прогнозирования.

Рекомендуем обратить внимание на подборку курсов по системной аналитике. Если вы только начинаете осваивать профессию аналитика, курсы помогут понять основы и научиться работать с реальными данными. В них есть как теоретическая, так и практическая часть.