Регрессионный анализ: что это, как работает и где применяется
Регрессионный анализ — это один из ключевых инструментов аналитики, который позволяет находить закономерности и прогнозировать результаты на основе данных. Он применяется в бизнесе, науке, экономике и машинном обучении, помогая понять, как изменение одной переменной влияет на другую. В этом курсе мы разбираем, что такое регрессионный анализ, как он работает и как его использовать для построения точных моделей прогнозирования.

Материал объясняет основные виды регрессии — линейную, множественную, логистическую и полиномиальную, — а также показывает, где этот метод эффективнее других. Мы также рассмотрим примеры из реальных задач и расскажем, какие инструменты помогут автоматизировать анализ.
- Инструменты регрессионного анализа
- Где применяется
- Как работает регрессионный анализ
- Чем отличается регрессия от корреляции
- Основные виды
- Условия и ограничения
- Этапы проведения регрессионного анализа
- Пример применения
- Какие инструменты использовать для регрессионного анализа
- Частые ошибки и как их избежать
- Рекомендуем посмотреть курсы по системной аналитике
- Заключение
Инструменты регрессионного анализа
В ходе регрессионного анализа строится математическая модель, описывающая природу взаимосвязи между независимыми и зависимыми variable. Это позволяет не только понять характер связи, но и делать прогнозы – например, как изменится спрос на товар при изменении цены.
Ключевые инструменты регрессионного анализа:
- Линейная регрессия
- Множественная регрессия
- Полиномиальная регрессия
- Логистическая регрессия
- Регуляризация (Ридж, Лассо)
На схеме представлена базовая идея регрессионного анализа. Изменения в независимых переменных (X) оказывают влияние на зависимую переменную (Y). Стрелка символизирует направленную связь, где независимые факторы служат причинами, а зависимая переменная — следствием
Какой бы сложностью не обладал регрессионный анализ в своем математическом аппарате, его цель проста: найти закономерности и построить model, которая максимально точно описывает реальные данные. В эпоху развития машинного обучения и искусственного интеллекта значимость этого метода только возрастает.
Где применяется
Регрессионный анализ — не просто теоретическая концепция, а инструмент, широко используемый в различных сферах. Давайте рассмотрим основные области его применения, где способность предсказывать одни variable на основе других превращается в существенное конкурентное преимущество.
Бизнес и маркетинг
В коммерческой сфере регрессионный анализ становится основой для принятия стратегических решений. Компании используют его для прогнозирования объемов продаж в зависимости от маркетинговых затрат, сезонности и других факторов. Например, розничная сеть может определить, как влияет расположение магазина, ассортимент и ценовая политика на конечную выручку.
Маркетологи применяют regression для оценки эффективности рекламных кампаний — насколько увеличились продажи в ответ на каждый вложенный в рекламу рубль? А также для сегментации клиентов и прогнозирования их поведения.
Экономика и финансы
В экономических исследованиях регрессионный анализ используется для выявления факторов, влияющих на макроэкономические показатели. Финансовые аналитики применяют regression для прогнозирования курсов валют, оценки риска инвестиций и управления портфелями активов.
Банки используют регрессионные model для оценки кредитоспособности заемщиков, выявляя зависимость между характеристиками клиента и вероятностью возврата кредита.
Медицина и биология
В медицинских исследованиях регрессионный анализ помогает выявлять факторы риска различных заболеваний. Например, можно определить, как образ жизни, генетические предрасположенности и окружающая среда влияют на вероятность развития сердечно-сосудистых заболеваний.
Фармацевтические компании используют регрессию для анализа эффективности лекарственных препаратов, оценивая зависимость между дозировкой и лечебным эффектом.
Data Science и машинное обучение
В сфере искусственного интеллекта регрессионный анализ — один из фундаментальных методов. Он используется как самостоятельно, так и в составе более сложных алгоритмов машинного обучения.
Модели regression помогают в обработке больших данных, обнаружении аномалий, прогнозировании временных рядов и создании рекомендательных систем — от прогноза погоды до рекомендаций товаров в интернет-магазинах.
Примечательно, что в эпоху глубокого обучения и нейронных сетей, регрессионный анализ сохраняет свою актуальность благодаря интерпретируемости результатов — мы можем не только получить прогноз, но и понять, почему model пришла к такому выводу.
Как работает регрессионный анализ
Для тех, кто не погружался в глубины статистики, регрессионный анализ может показаться сложным инструментом. Однако его основная идея достаточно проста: найти такую математическую формулу, которая наилучшим образом описывает взаимосвязь между variable. Давайте разберем ключевые элементы этого процесса.
| Термин | Объяснение |
|---|---|
| Зависимая переменная | Это показатель, который мы пытаемся предсказать или объяснить. В формулах обычно обозначается как y. Например, цена дома, которую мы хотим предсказать. |
| Независимая переменная | Фактор, который, как мы предполагаем, влияет на зависимую переменную. Обозначается как x. В примере с домом это может быть площадь, количество комнат, расположение. |
| Уравнение регрессии | Математическая формула, описывающая связь между переменными. Для линейной regression это y = b₀ + b₁x₁ + b₂x₂ + … + ε, где b — коэффициенты, а ε — случайная ошибка. |
| Коэффициенты регрессии | Числа, показывающие силу и направление влияния каждой независимой переменной. Например, b₁ = 5 означает, что увеличение x₁ на единицу приводит к увеличению y в среднем на 5 единиц. |
| Свободный член | Значение b₀, показывающее, чему равна зависимая переменная, когда все независимые variable равны нулю. |
| Случайная ошибка | Компонент ε, учитывающий влияние неизвестных или неучтенных факторов, а также случайные колебания. |
Процесс построения регрессионной model можно сравнить с настройкой музыкального инструмента — мы подбираем коэффициенты так, чтобы модель максимально точно «звучала» в унисон с реальными данными. Для этого используется метод наименьших квадратов, который минимизирует сумму квадратов отклонений прогнозируемых значений от фактических.
Важно понимать, что регрессия не просто находит связь между переменными, но и количественно оценивает эту связь. Это позволяет не только констатировать, что «площадь влияет на цену дома», но и сказать, что «увеличение площади на 10 кв. м приводит к повышению цены в среднем на 500 000 рублей».
Результат регрессионного анализа — model, которая позволяет как интерпретировать влияние факторов, так и делать прогнозы для новых наблюдений. Например, имея уравнение regression для цены дома, мы можем оценить стоимость жилья с определенными характеристиками, которое только выходит на рынок.
Чем отличается регрессия от корреляции
В аналитических исследованиях нередко возникает путаница между понятиями регрессии и корреляции. Оба метода работают с взаимосвязями между variable, однако имеют принципиальные различия в целях, подходах и интерпретации результатов.
| Аспект | Корреляция | Регрессия |
|---|---|---|
| Цель | Измерение силы и направления связи между переменными | Моделирование зависимости одной переменной от других и прогнозирование |
| Результат | Коэффициент корреляции (от -1 до +1) | Уравнение с коэффициентами, описывающее зависимость |
| Отношения переменных | Симметричные (переменные равноправны) | Асимметричные (выделяются зависимая и независимые переменные) |
| Причинность | Не устанавливает причинно-следственных связей | Предполагает влияние независимых переменных на зависимую |
| Прогнозирование | Не предназначена для прогнозирования | Позволяет делать прогнозы при известных значениях независимых переменных |
Важно понимать, что корреляция показывает лишь наличие статистической связи, но не объясняет ее природу. Классический пример — корреляция между продажами мороженого и количеством утонувших людей. Обе величины возрастают летом, но не потому что одна влияет на другую, а потому что существует третий фактор — жаркая погода.
В то же время regression идет дальше и пытается установить, как именно одна переменная влияет на другую. Она предполагает направленную связь: независимые variable рассматриваются как причины, а зависимая — как следствие. Регрессионная модель позволяет сказать: «если независимая переменная изменится на столько-то, то зависимая, скорее всего, изменится вот так».
Впрочем, и регрессия сама по себе не доказывает причинно-следственных связей. Для установления причинности требуются дополнительные исследования, включая контролируемые эксперименты. Как говорят статистики: «Корреляция не означает причинность, а regression не доказывает причинность».
Таким образом, корреляционный анализ можно рассматривать как первый шаг в исследовании связей между переменными, а регрессионный — как следующий этап, позволяющий построить математическую model этой связи и использовать ее для прогнозирования.
Основные виды
В арсенале современного аналитика существует множество вариаций регрессионного анализа, каждая из которых имеет свои особенности и области применения. Разберем основные виды, с которыми чаще всего приходится работать специалистам по данным.
Линейная регрессия
Самый базовый и распространенный вид regression, предполагающий линейную зависимость между variable. Уравнение имеет вид:
y = β₀ + β₁x + ε
где y — зависимая переменная, x — независимая, β₀ — свободный член, β₁ — коэффициент наклона прямой, ε — случайная ошибка.
Линейная регрессия привлекательна своей простотой и интерпретируемостью. График такой зависимости представляет собой прямую линию, которая наилучшим образом аппроксимирует наблюдения. Несмотря на кажущуюся примитивность, этот метод остается мощным инструментом для анализа данных и часто служит отправной точкой для более сложных model.
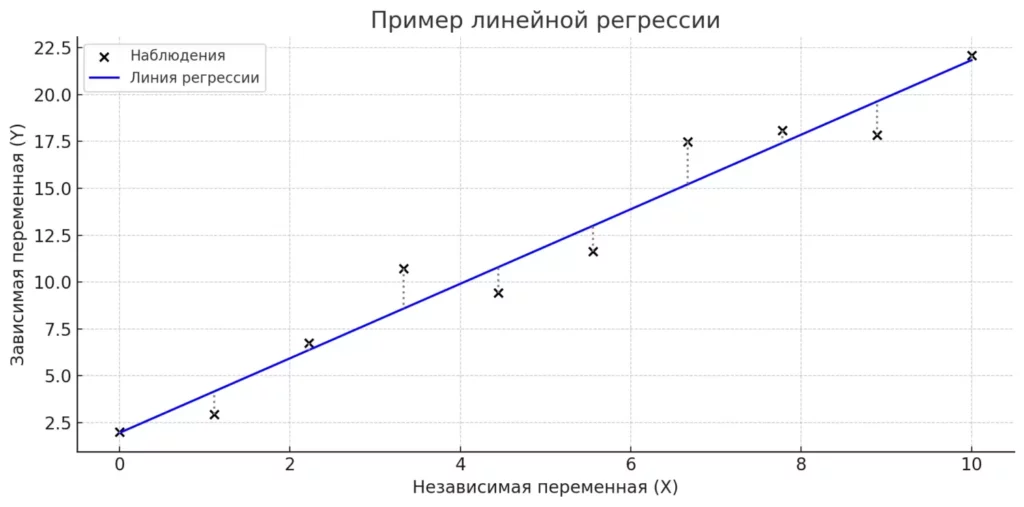
На графике показан пример работы линейной regression. Черные крестики обозначают фактические наблюдения (реальные данные), а синяя прямая линия — это линия регрессии, которая аппроксимирует зависимость между variable. Пунктирные серые линии иллюстрируют отклонения наблюдаемых значений от предсказанных моделью (остатки)
Множественная линейная регрессия
Расширение линейной regression на случай, когда независимых переменных несколько:
y = β₀ + β₁x₁ + β₂x₂ + … + βₙxₙ + ε
Этот метод позволяет учесть влияние множества факторов одновременно. Например, при оценке стоимости недвижимости можно учитывать площадь, количество комнат, этаж, удаленность от метро и другие характеристики. Каждый коэффициент βᵢ показывает, как изменится зависимая переменная при изменении соответствующей независимой переменной на единицу (при условии, что остальные переменные остаются неизменными).
Полиномиальная регрессия
Когда зависимость между variable нелинейна, на помощь приходит полиномиальная regression:
y = β₀ + β₁x + β₂x² + … + βₙxⁿ + ε
Здесь независимая переменная используется в различных степенях, что позволяет моделировать более сложные зависимости — параболические, кубические и т.д. Интересно, что математически полиномиальная регрессия может быть сведена к множественной линейной регрессии, если рассматривать каждую степень x как отдельную переменную.
Логистическая регрессия
Вопреки названию, логистическая регрессия используется для решения задач классификации, а не regression в чистом виде. Она моделирует вероятность того, что наблюдение принадлежит к определенному классу:
p(y=1) = 1 / (1 + e^(-(β₀ + β₁x₁ + … + βₙxₙ)))
Результат логистической регрессии — вероятность от 0 до 1. Этот метод широко применяется в медицине (вероятность заболевания), финансах (вероятность дефолта) и маркетинге (вероятность покупки).
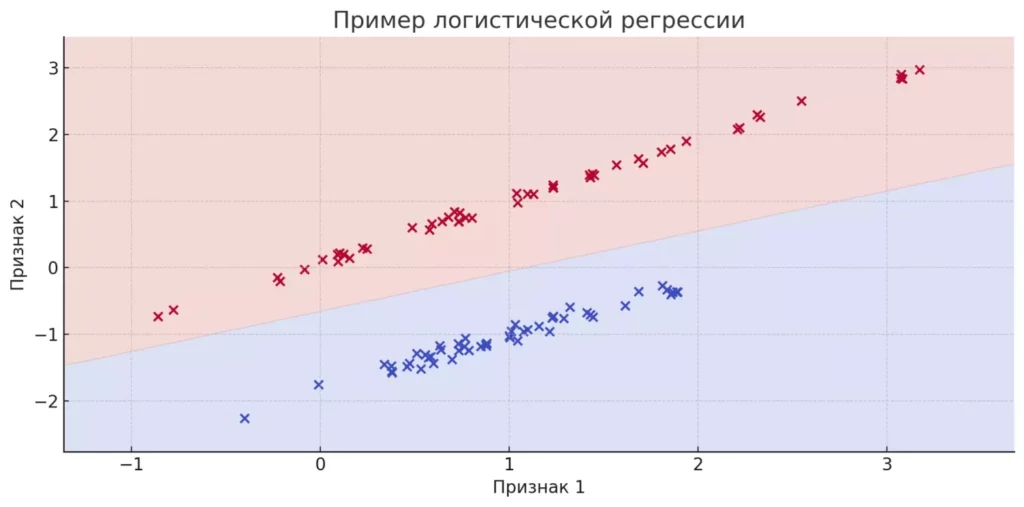
На графике изображен пример работы логистической регрессии для задачи бинарной классификации. Две группы точек различаются цветом: одна группа (например, класс 0) выделена синим цветом, другая (класс 1) — красным. Светло-синие и светло-красные области показывают зоны, где model прогнозирует принадлежность к тому или иному классу. Разделяющая линия на границе цветов — это граница принятия решений, определяемая логистической regression.
Другие виды регрессии
- Ридж-регрессия (L2-регуляризация) добавляет штраф за большие значения коэффициентов, что помогает бороться с мультиколлинеарностью и переобучением.
- Лассо-регрессия (L1-регуляризация) также штрафует за большие коэффициенты, но может полностью обнулять некоторые из них, тем самым выполняя отбор признаков.
- Эластичная сеть комбинирует подходы Ридж и Лассо для получения лучших результатов.
- Квантильная регрессия моделирует медиану или другие квантили распределения зависимой переменной, что делает ее устойчивой к выбросам.
- Нелинейная регрессия использует более сложные функциональные зависимости, которые не сводятся к линейным комбинациям variable.
Выбор конкретного вида regression зависит от природы исследуемых данных, типа решаемой задачи и требований к интерпретируемости модели. Часто приходится экспериментировать с разными видами регрессии, чтобы найти оптимальный баланс между точностью и сложностью model.
Условия и ограничения
Регрессионный анализ, при всей своей мощи и универсальности, не является панацеей. Для получения надежных и интерпретируемых результатов необходимо соблюдение ряда условий. Когда мы игнорируем эти предпосылки, model могут давать некорректные результаты, приводя к ошибочным выводам и прогнозам.
Линейность
Условие:
Зависимость между переменными должна быть линейной или приводимой к линейной форме.
Проблема при нарушении:
Если истинная зависимость нелинейна, линейная model будет систематически ошибаться. Представьте, что вы пытаетесь описать параболу прямой линией — очевидно, что ни в одной точке, кроме пересечений, эта аппроксимация не будет точной.
Решение:
Использовать нелинейные преобразования variable или нелинейные модели regression.
Отсутствие мультиколлинеарности
Условие:
Независимые переменные не должны сильно коррелировать между собой.
Проблема при нарушении:
Мультиколлинеарность приводит к нестабильности оценок коэффициентов регрессии. Небольшие изменения в данных могут приводить к значительным изменениям в model, что затрудняет интерпретацию.
Решение:
Исключить одну из коррелирующих variable, использовать Ридж-regression или метод главных компонент для преобразования переменных.
Нормальность остатков
Условие:
Остатки (разности между фактическими и предсказанными значениями) должны быть распределены нормально.
Проблема при нарушении:
Доверительные интервалы и статистические тесты для коэффициентов становятся ненадежными.
Решение:
Применить преобразования к зависимой переменной (например, логарифмирование) или использовать робастные методы оценки.
Гомоскедастичность
Условие:
Дисперсия остатков должна быть постоянной для всех значений независимых variable.
Проблема при нарушении:
Гетероскедастичность (непостоянная дисперсия) приводит к неэффективности оценок и неправильным стандартным ошибкам коэффициентов.
Решение:
Использовать взвешенный метод наименьших квадратов или робастные стандартные ошибки.
Независимость наблюдений
Условие:
Наблюдения должны быть независимыми друг от друга.
Проблема при нарушении:
Автокорреляция (в временных рядах) или пространственная корреляция приводят к неэффективным оценкам и неправильным выводам о статистической значимости.
Решение:
Применять методы для работы с временными рядами (ARIMA) или учитывать структуру зависимости в model.
Важно понимать, что в реальных задачах редко удается полностью соблюсти все условия. Регрессионный анализ оказывается достаточно устойчивым к умеренным нарушениям предпосылок. Однако при серьезных отклонениях необходимо либо модифицировать данные, либо выбирать альтернативные методы моделирования.
Проверка соблюдения условий регрессионного анализа — важный этап моделирования, которым не следует пренебрегать. Современные статистические пакеты предлагают множество диагностических инструментов, от графического анализа остатков до формальных статистических тестов, которые помогают выявить нарушения предпосылок.
Этапы проведения регрессионного анализа
Регрессионный анализ — это не просто применение формулы к набору данных, а целый процесс, требующий методичного подхода. Чтобы получить надежные и интерпретируемые результаты, необходимо пройти несколько ключевых этапов. Рассмотрим пошаговый алгоритм проведения регрессионного анализа.
- Постановка задачи и определение целей
Первый шаг — четко сформулировать, что именно мы хотим узнать. Какую зависимую переменную нужно предсказать? Какие факторы могут на нее влиять? Будем ли мы использовать model для прогнозирования или для понимания структуры зависимостей? Ответы на эти вопросы определят выбор подхода к анализу. - Сбор данных
На этом этапе собираются все необходимые данные для анализа. Важно убедиться, что выборка репрезентативна и достаточно велика для получения статистически значимых результатов. Недостаточный объем данных может привести к нестабильным оценкам коэффициентов. - Разведочный анализ данных
Перед построением модели необходимо тщательно изучить данные: построить графики распределений variable, диаграммы рассеяния, проверить наличие выбросов и пропущенных значений. Этот этап помогает выявить потенциальные проблемы и сформировать первоначальное представление о характере зависимостей. - Подготовка и преобразование данных
На основе разведочного анализа проводится обработка данных: заполнение пропусков, обработка выбросов, стандартизация или нормализация переменных, преобразование категориальных переменных в числовые. Иногда требуется трансформировать variable для достижения линейности зависимости (например, логарифмирование). - Выбор модели регрессии
Исходя из характера данных и поставленной задачи, выбирается тип регрессионной model: линейная, полиномиальная, логистическая или другая. Также определяется набор независимых variable, которые будут включены в модель. - Обучение модели
Модель «обучается» на подготовленных данных. Для этого используются различные алгоритмы, например, метод наименьших квадратов. В результате определяются значения коэффициентов regression, которые минимизируют ошибку между предсказанными и фактическими значениями. - Оценка качества модели
После обучения необходимо оценить, насколько хорошо model описывает данные. Для этого используются различные метрики: коэффициент детерминации (R²), среднеквадратичная ошибка (RMSE), средняя абсолютная ошибка (MAE) и другие. Также проводится анализ остатков для проверки соблюдения предпосылок регрессионного analysis. - Интерпретация результатов
На этом этапе анализируются полученные коэффициенты regression, их статистическая значимость и доверительные интервалы. Это позволяет понять, какие факторы оказывают наибольшее влияние на зависимую переменную и как именно. - Проверка модели на тестовых данных
Для оценки обобщающей способности модели часто используется кросс-валидация или проверка на отдельной тестовой выборке. Это помогает выявить переобучение модели и оценить, насколько хорошо она будет работать на новых данных. - Применение модели и мониторинг
Финальная model применяется для прогнозирования или analysis. Важно периодически оценивать ее актуальность, так как со временем характер зависимостей может измениться, и модель потребует переобучения или корректировки.
Следование этому структурированному подходу помогает максимизировать ценность регрессионного analysis и избежать типичных ошибок. Хотя в некоторых случаях отдельные этапы могут быть объединены или модифицированы, общая логика процесса остается неизменной.
Пример применения
Чтобы лучше понять, как работает регрессионный analysis на практике, рассмотрим конкретный пример. Представим, что мы занимаемся оценкой недвижимости и хотим создать модель для прогнозирования цен на квартиры.
Постановка задачи
У нас есть данные о продажах квартир в определенном городе. Наша цель — построить model, которая позволит оценивать стоимость квартир на основе их характеристик.
Исходные данные
Допустим, мы собрали информацию о следующих параметрах:
- Площадь квартиры (x₁) в квадратных метрах
- Количество комнат (x₂)
- Этаж (x₃)
- Расстояние до центра города (x₄) в километрах
- Цена квартиры (y) в тысячах рублей
Разведочный анализ
Начнем с визуализации данных. На диаграмме рассеяния видно, что существует положительная корреляция между площадью квартиры и ценой, отрицательная — между расстоянием до центра и ценой. Также заметим, что распределение цен имеет правостороннюю асимметрию, что подсказывает возможность логарифмического преобразования.
Выбор и построение модели
Начнем с построения множественной линейной regression:
y = β₀ + β₁x₁ + β₂x₂ + β₃x₃ + β₄x₄ + ε
Применив метод наименьших квадратов к нашим данным, получаем следующие оценки коэффициентов:
- β₀ = -3,33 (свободный член)
- β₁ = 5,33 (коэффициент при площади)
- β₂ = 13,33 (коэффициент при количестве комнат)
- β₃ = 2,5 (коэффициент при этаже)
- β₄ = -7,1 (коэффициент при расстоянии до центра)
Итоговое уравнение регрессии:
y ≈ -3,33 + 5,33x₁ + 13,33x₂ + 2,5x₃ — 7,1x₄
Интерпретация модели
Это уравнение можно интерпретировать следующим образом:
- Увеличение площади на 1 кв. м приводит к увеличению цены в среднем на 5,33 тыс. руб. (при прочих равных условиях)
- Дополнительная комната увеличивает цену в среднем на 13,33 тыс. руб.
- Каждый этаж выше добавляет к цене в среднем 2,5 тыс. руб.
- Каждый дополнительный километр от центра города снижает цену в среднем на 7,1 тыс. руб.
Оценка качества модели
Для нашей model коэффициент детерминации R² составил 0,82. Это означает, что модель объясняет 82% вариации цен на квартиры, что является достаточно хорошим показателем.
Применение модели для прогнозирования
Теперь мы можем использовать полученную model для оценки стоимости квартир. Например, для квартиры со следующими характеристиками:
- Площадь: 60 кв. м
- Количество комнат: 2
- Этаж: 5
- Расстояние до центра: 3 км
Подставляем эти значения в уравнение:
y ≈ -3,33 + 5,33 × 60 + 13,33 × 2 + 2,5 × 5 — 7,1 × 3 ≈ 334,97
Таким образом, предполагаемая стоимость этой квартиры составляет около 335 тыс. руб.
Ограничения модели
Важно отметить, что наша model имеет ряд ограничений:
- Она учитывает только количественные факторы, игнорируя такие аспекты, как состояние дома, инфраструктура района и т.д.
- Модель предполагает линейную зависимость, хотя в реальности она может быть более сложной.
- Прогнозы model становятся менее надежными для квартир с характеристиками, значительно отличающимися от средних в обучающей выборке.
Этот пример демонстрирует, как регрессионный analysis позволяет не только построить модель для прогнозирования, но и количественно оценить влияние различных факторов на целевую переменную. В реальных задачах процесс может быть более сложным, включая дополнительные этапы преобразования данных, отбора признаков и проверки качества model.
Какие инструменты использовать для регрессионного анализа
В современном мире аналитики данных имеют в распоряжении широкий спектр инструментов для проведения регрессионного analysis — от простых электронных таблиц до специализированных статистических пакетов и библиотек программирования. Выбор инструмента зависит от сложности задачи, объема данных и уровня технической подготовки аналитика.
| Инструмент | Преимущества | Ограничения | Пример использования |
|---|---|---|---|
| Microsoft Excel | Доступность, интуитивно понятный интерфейс, не требует навыков программирования | Ограниченные возможности для сложных моделей, проблемы с большими объемами данных | =ЛИНЕЙН(B2:B100;A2:A100;ИСТИНА;ИСТИНА) для построения линейной регрессии |
| Python (scikit-learn) | Гибкость, мощные возможности визуализации, интеграция с другими инструментами analysis данных | Требует знания программирования, более высокий порог вхождения | from sklearn.linear_model import LinearRegression
`model = LinearRegression()` `model.fit(X, y)` |
| Python (statsmodels) | Подробная статистическая информация, фокус на статистической интерпретации | Требует знания программирования и статистики | import statsmodels.api as sm
`model = sm.OLS(y, sm.add_constant(X))` `results = model.fit()` |
| R | Специализированный язык для статистического анализа, богатая экосистема пакетов | Специфический синтаксис, менее универсален чем Python | model <- lm(price ~ area + rooms, data = housing_data)
`summary(model)` |
| SPSS | Удобный графический интерфейс, не требует глубоких знаний программирования | Высокая стоимость лицензии, менее гибкий в сравнении с языками программирования | Через меню: Analyze > Regression > Linear |
| Tableau | Мощные возможности визуализации, интерактивные дашборды | Ограниченная функциональность для сложного статистического analysis | Использование встроенной функции линейного тренда для аналитики |
| PowerBI | Интеграция с экосистемой Microsoft, доступность для бизнес-пользователей | Ограниченные возможности для глубокого статистического анализа | Создание прогнозов с использованием встроенных аналитических функций |
Для начинающих аналитиков Excel может стать отличной отправной точкой — он позволяет быстро построить простые регрессионные model и визуализировать результаты. По мере роста сложности задач и объема данных стоит обратить внимание на специализированные инструменты.
Для тех, кто готов инвестировать время в изучение программирования, Python предлагает наилучший баланс между доступностью и функциональностью. Библиотека scikit-learn ориентирована на машинное обучение и предлагает широкий набор инструментов для регрессионного analysis, в то время как statsmodels фокусируется на статистической интерпретации.
R традиционно считается языком статистиков и предлагает богатый набор пакетов для регрессионного analysis, включая специализированные инструменты для различных видов regression, диагностики и визуализации.
Для бизнес-пользователей, которым нужно быстро создавать интерактивные отчеты и дашборды на основе регрессионного analysis, платформы бизнес-аналитики, такие как Tableau и PowerBI, могут быть оптимальным выбором, хотя их возможности для глубокого статистического анализа ограничены.
В конечном счете, выбор инструмента должен соответствовать конкретной задаче, доступным ресурсам и навыкам пользователя. Часто наилучшим подходом является комбинация нескольких инструментов на разных этапах analysis.
Частые ошибки и как их избежать
При проведении регрессионного analysis даже опытные специалисты могут сталкиваться с типичными проблемами, которые способны привести к некорректным выводам. Знание этих подводных камней помогает выстроить правильную методологию и получить надежные результаты.
Переобучение модели
Ошибка:
Модель слишком хорошо «запоминает» обучающие данные, включая шум, но плохо обобщает закономерности на новых данных.
Признаки:
Очень высокий R² на обучающей выборке, но низкая точность на тестовой; большое количество variable относительно объема данных.
Решение:
Разделять данные на обучающую и тестовую выборки; использовать кросс-валидацию; применять регуляризацию (Ridge, Lasso); сокращать количество переменных в model .
Игнорирование мультиколлинеарности
Ошибка:
Включение в модель сильно коррелирующих друг с другом независимых variable.
Признаки:
Нестабильные коэффициенты regression; коэффициенты меняют знак при небольших изменениях данных; высокие стандартные ошибки коэффициентов.
Решение:
Рассчитывать коэффициенты корреляции между переменными и VIF (фактор инфляции дисперсии); исключать или объединять сильно коррелирующие variable; применять методы снижения размерности (PCA).
Игнорирование влияния выбросов
Ошибка:
Включение экстремальных значений, которые могут искажать результаты regression.
Признаки:
Значительное изменение коэффициентов при удалении нескольких наблюдений; необычно высокие значения остатков для некоторых наблюдений.
Решение:
Визуализировать данные для выявления выбросов; использовать робастные методы regression; трансформировать переменные (например, логарифмирование) для уменьшения влияния выбросов.
Неправильная спецификация модели
Ошибка:
Выбор неподходящего типа регрессионной model или неверный набор переменных.
Признаки:
Систематические паттерны в остатках; низкий R² несмотря на теоретически обоснованные переменные.
Решение:
Использовать разведочный analysis данных для понимания характера зависимостей; тестировать различные функциональные формы (линейные, логарифмические, полиномиальные); включать взаимодействия между переменными, если это имеет смысл.
Ошибки при интерпретации результатов
Ошибка:
Путаница между корреляцией и причинно-следственной связью; некорректная интерпретация коэффициентов.
Признаки:
Выводы о причинно-следственных связях без дополнительных доказательств; неучет контекста при интерпретации.
Решение:
Помнить, что regression показывает ассоциации, но не доказывает причинность; учитывать возможное влияние пропущенных variable; проверять, соответствуют ли результаты теоретическим ожиданиям и предыдущим исследованиям.
Недостаточная проверка предпосылок
Ошибка:
Игнорирование требований к данным для применения регрессионного analysis.
Признаки:
Некорректные доверительные интервалы и p-значения; ненадежные прогнозы.
Решение:
Проводить формальные тесты на нормальность остатков, гомоскедастичность, отсутствие автокорреляции; визуализировать остатки для выявления нарушений предпосылок.
При проведении регрессионного анализа важно помнить, что это не механический процесс, а аналитический метод, требующий критического мышления на каждом этапе. Комбинирование статистических тестов, визуализации данных и предметных знаний позволяет избежать типичных ошибок и получить надежные и интерпретируемые результаты.
Теоретическое понимание регрессионного analysis — это важный первый шаг, но для полноценного овладения методом необходима практика под руководством опытных специалистов. Если вы заинтересованы в углублении своих знаний и навыков в области аналитики данных, стоит обратить внимание на специализированные образовательные программы. Курсы системного аналитика помогут не только освоить регрессионный анализ, но и изучить другие важные методы и инструменты работы с данными. На странице лучших курсов системного аналитика вы найдете образовательные программы различного уровня сложности, которые помогут вам перейти от теории к практике и стать востребованным специалистом по анализу данных.
Рекомендуем посмотреть курсы по системной аналитике
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Аналитик данных
|
Eduson Academy
83 отзыва
|
Цена
Ещё -5% по промокоду
99 760 ₽
|
От
8 313 ₽/мес
Беспроцентная. На 1 год.
|
Длительность
6 месяцев
|
Старт
6 января
|
Ссылка на курс |
|
Системный и бизнес-анализ в разработке ПО. Интенсив
|
Level UP
36 отзывов
|
Цена
75 000 ₽
|
От
18 750 ₽/мес
|
Длительность
1 месяц
|
Старт
26 декабря
|
Ссылка на курс |
|
Системный аналитик PRO
|
Нетология
45 отзывов
|
Цена
с промокодом kursy-online
79 800 ₽
140 000 ₽
|
От
3 500 ₽/мес
Рассрочка на 2 года.
|
Длительность
10 месяцев
|
Старт
13 января
|
Ссылка на курс |
|
Системный аналитик с нуля
|
Stepik
33 отзыва
|
Цена
4 500 ₽
|
|
Длительность
1 неделя
|
Старт
в любое время
|
Ссылка на курс |
|
Системный аналитик с нуля до PRO
|
Eduson Academy
83 отзыва
|
Цена
Ещё -11% по промокоду
119 760 ₽
257 760 ₽
|
От
9 980 ₽/мес
10 740 ₽/мес
|
Длительность
6 месяцев
|
Старт
в любое время
|
Ссылка на курс |
Заключение
Регрессионный analysis — универсальный и мощный инструмент, который находит применение в различных областях: от бизнес-аналитики до научных исследований. Несмотря на свою математическую основу, он остается интуитивно понятным методом для понимания взаимосвязей между variable и построения прогнозов.
В нашем обзоре мы рассмотрели основные концепции регрессионного analysis, различные его виды и области применения. Мы увидели, что правильный подход к построению регрессионных model включает тщательный analysis данных, выбор подходящего типа regression, проверку предпосылок и интерпретацию результатов.
Важно помнить, что regression — это не просто технический метод, но и способ мышления о данных и взаимосвязях в них. Умение видеть ограничения моделей и интерпретировать результаты в контексте предметной области часто оказывается важнее, чем техническое совершенство самой model.
С развитием машинного обучения и искусственного интеллекта появляются все более сложные алгоритмы прогнозирования. Однако классический регрессионный анализ сохраняет свою ценность благодаря интерпретируемости и простоте использования. Он продолжает оставаться фундаментальным инструментом в арсенале каждого аналитика данных.
Освоение регрессионного analysis — важный шаг на пути к пониманию более сложных методов анализа данных и машинного обучения. Начните с простых model, постепенно увеличивая их сложность, и вы обнаружите, что этот метод может дать удивительно глубокое понимание закономерностей в данных вашей сферы деятельности.

Как работать с модулем random в Python
Хотите понять, зачем нужен модуль random Python и как выбрать нужное распределение? Получите краткие советы по настройке seed и применению функций для реальных задач.

Альтернативы Docker: полный обзор зарубежных и российских решений
Ищете альтернативы Docker и не знаете, что выбрать? В статье вы найдете обзор инструментов для контейнеризации, сравнение их возможностей и практические советы для разных задач.

Sublime Text — что это за редактор кода и как им пользоваться
Хотите понять, sublime text как пользоваться в работе разработчика? В статье собраны полезные примеры, настройки и приёмы, которые сделают работу быстрее и удобнее.

Infrastructure as Code: автоматизация для DevOps
Infrastructure as Code позволяет описывать инфраструктуру кодом, автоматизируя процессы и снижая риски ошибок. Как внедрить и что выбрать?