Что такое деление в Python и как оно работает
В мире программирования деление — это нечто большее, чем простая математическая операция. Для разработчика на Python понимание различных способов дробления открывает целый арсенал инструментов для решения разнообразных задач: от финансовых расчетов до алгоритмической оптимизации. В этом курсе мы детально рассмотрим все аспекты деления в Python и научимся применять их в реальных сценариях разработки.

Python предлагает три основных оператора деления, каждый со своими особенностями: обычное (/), целочисленное (//) и получение остатка (%). Эти операторы взаимодействуют с тремя типами чисел: целыми (int), с плавающей точкой (float) и комплексными (complex).
Почему это важно? Представьте, что вы разрабатываете финансовое приложение. При работе с деньгами разница между 5/2 = 2.5 и 5//2 = 2 может означать не просто математическую неточность, а реальную финансовую ошибку. Или, возможно, вы создаете алгоритм распределения ресурсов, где остаток (%) поможет равномерно распределить задачи между исполнителями.
Понимание нюансов дробления в Python — это не академическое упражнение, а практический навык, который делает код более точным, эффективным и свободным от неожиданных ошибок.
- Типы чисел и влияние типа на результат
- Комплексные числа (complex)
- Целочисленное (//)
- Остаток (%)
- Деление на ноль и как его избежать
- Сокращённая запись операций деления (/=, //=, %=)
- Частые ошибки при делении и советы
- Заключение
Типы чисел и влияние типа на результат
Прежде чем погрузиться в операторы деления, важно понять, с какими числовыми типами мы имеем дело в Python. Тип операндов (чисел, участвующих в дроблении) напрямую влияет на тип результата, что может иметь критическое значение для работы алгоритма.
Целые числа (int)
Целые числа в Python представляют собой положительные и отрицательные числа без дробной части. Уникальной особенностью Python является отсутствие ограничения на размер целых чисел — они могут быть произвольно большими, ограниченными лишь доступной памятью.
x = 42 y = -17 huge_number = 10**100 # Гугол - число с 100 нулями
Числа с плавающей точкой (float)
Числа с плавающей точкой представляют значения с дробной частью. В Python они соответствуют стандарту IEEE 754, что приводит к интересным особенностям при вычислениях:
precise = 1.5 scientific = 2.5e3 # 2500.0 (научная нотация)
Важно отметить, что работа с float может приводить к незначительным погрешностям из-за особенностей представления дробных чисел в двоичной системе:
print(0.1 + 0.2) # 0.30000000000000004, а не 0.3
Комплексные числа (complex)
Комплексные числа содержат действительную и мнимую части. В Python они определяются как a + bj, где a и b — действительные числа, а j — мнимая единица:
z = 3 + 4j
При дроблении комплексных чисел результатом также будет комплексное число, что отражает математические правила операций с комплексными числами.
Как тип влияет на деление
Когда мы используем оператор дробления в Python, тип результата определяется сложным взаимодействием типов операндов и используемого оператора:
- При обычном (/) двух целых чисел результат всегда будет float, даже если деление происходит без остатка: 4 / 2 даст 2.0, а не 2.
- При целочисленном (//) тип результата соответствует типу операндов: 5 // 2 даст 2 (тип int), но 5.0 // 2 или 5 // 2.0 дадут 2.0 (тип float).
- При вычислении остатка (%) правила аналогичны целочисленному делению.
Это поведение, введенное в Python 3, обеспечивает более предсказуемые результаты по сравнению с Python 2, где дробление целых чисел всегда давало целый результат, что могло приводить к неожиданным ошибкам в расчетах.
Обычное (/)
Оператор обычного деления (/) в Python выполняет стандартную математическую операцию с сохранением дробной части. Этот оператор — базовый инструмент для любых вычислений, где требуется точный результат.
Примеры использования
Рассмотрим, как работает обычное дробление с разными типами чисел:
print(10 / 5) # 2.0 print(5 / 2) # 2.5 print(1 / 3) # 0.3333333333333333 print(-7 / 2) # -3.5
Заметьте интересную особенность: даже если результат деления — целое число (как в случае 10 / 5), Python все равно возвращает его в формате float (с плавающей точкой). Это единообразное поведение помогает избежать ошибок, которые могли бы возникнуть при смешении типов данных.
| Операнды | Выражение | Результат | Тип результата |
|---|---|---|---|
| int / int | 5 / 2 | 2.5 | float |
| float / int | 5.0 / 2 | 2.5 | float |
| int / float | 5 / 2.0 | 2.5 | float |
| float / float | 5.0 / 2.0 | 2.5 | float |
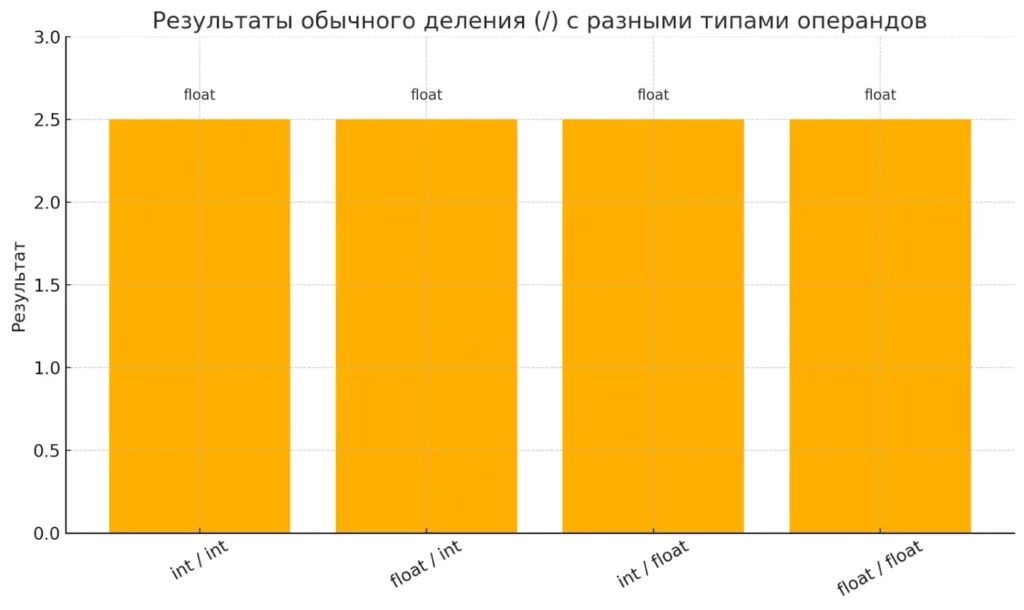
График показывает, что несмотря на различия типов операндов, результат обычного деления / всегда имеет тип float. Это подчёркивает единообразие поведения оператора / в Python 3.
Влияние версии Python 2 vs 3
В этом месте важно отметить существенное различие между Python 2 и Python 3. В Python 2 деление двух целых чисел давало целочисленный результат:
# Python 2 print(5 / 2) # 2 (целочисленный результат)
Это поведение часто приводило к ошибкам, особенно когда разработчики ожидали получить точный результат со всеми десятичными знаками. В Python 3 эта проблема была решена — теперь оператор / всегда выполняет «истинное деление» и возвращает результат с плавающей точкой.
Точность и округление (round)
При работе с дроблением в Python необходимо учитывать особенности представления чисел с плавающей точкой. Как мы уже упоминали, из-за представления чисел в двоичной системе некоторые десятичные дроби невозможно представить точно:
print(0.1 + 0.2) # 0.30000000000000004
Для решения проблем с точностью Python предлагает функцию round(), которая округляет число до указанного количества десятичных знаков:
print(round(1 / 3, 2)) # 0.33 print(round(0.1 + 0.2, 1)) # 0.3 print(round(123.456789, 2)) # 123.46
Для задач, требующих высокой точности (например, финансовых расчетов), рекомендуется использовать модуль decimal, который обеспечивает более точное представление десятичных дробей:
from decimal import Decimal
print(Decimal('0.1') + Decimal('0.2')) # 0.3
Обычное дробление — универсальный инструмент для большинства математических операций в Python. Однако в некоторых случаях, особенно когда нам нужно работать только с целыми частями чисел или остатками от деления, на сцену выходят другие операторы, которые мы рассмотрим в следующих разделах.
Целочисленное (//)
Оператор целочисленного дробления (//) — это инструмент, который позволяет получить результат деления без дробной части. В отличие от обычного, этот оператор возвращает только целую часть частного, отбрасывая любой остаток. В программировании такой подход часто необходим для работы с дискретными величинами, распределением ресурсов или при операциях с индексами и ключами.
Примеры положительных и отрицательных чисел
Рассмотрим, как работает целочисленное деление в различных сценариях:
print(10 // 3) # 3 print(7 // 2) # 3 print(5 // 5) # 1
Здесь важно отметить, что оператор // всегда округляет результат в сторону отрицательной бесконечности (математически это называется «округление вниз» или «целочисленное деление с округлением вниз»). Это особенно заметно при работе с отрицательными числами:
print(-7 // 2) # -4 (а не -3.5, округленное до -3) print(7 // -2) # -4 (а не -3.5, округленное до -3)
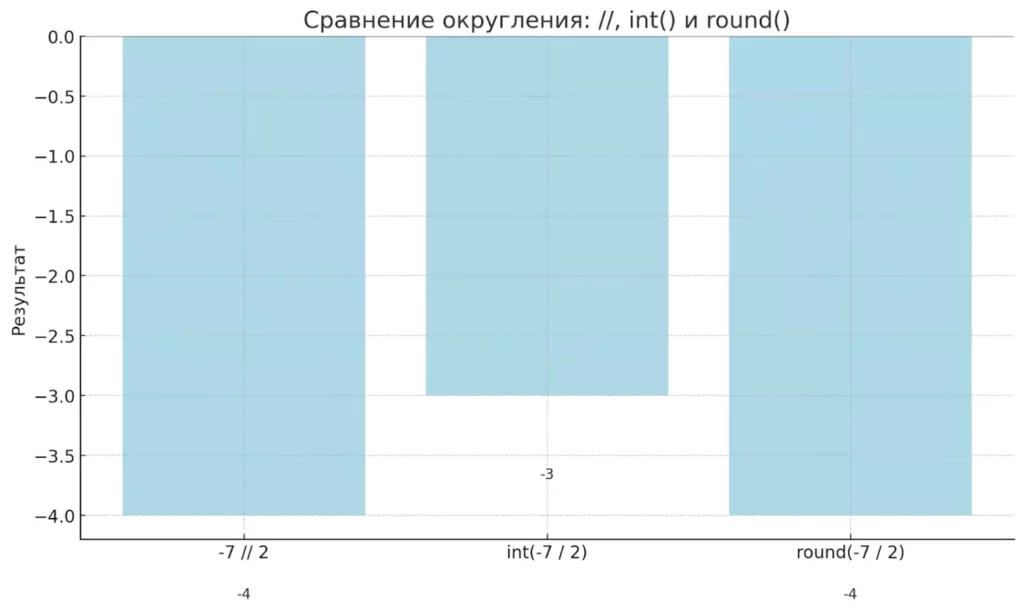
Разные подходы к округлению дробного результата в Python: // округляет вниз (в сторону минус бесконечности), int() — отбрасывает дробную часть, round() — округляет по стандартным правилам.
Данная особенность может стать источником ошибок, если не учитывать, что результат округляется именно вниз, а не по стандартным правилам округления к ближайшему целому. Рассмотрим сравнительную таблицу:
| Выражение | Полный результат | Целочисленное |
|---|---|---|
| 7 // 2 | 3.5 | 3 |
| -7 // 2 | -3.5 | -4 |
| 7 // -2 | -3.5 | -4 |
Что происходит с float типами
Когда в операции целочисленного деления участвует хотя бы одно число с плавающей точкой, Python сохраняет тип float для результата, но все равно отбрасывает дробную часть:
print(10.0 // 3) # 3.0 print(10 // 3.0) # 3.0 print(10.5 // 3.5) # 3.0
Это поведение согласуется с общим правилом: если один из операндов имеет тип float, результат также будет иметь тип float, даже если значение — целое число.
Целочисленное особенно полезно в следующих сценариях:
- Разбиение на группы:
Когда нужно узнать, сколько групп определенного размера можно сформировать
items = 23 group_size = 5 full_groups = items // group_size # 4 полные группы
- Преобразование времени:
Например, при конвертации секунд в минуты и часы
seconds = 3665 minutes = seconds // 60 # 61 минута hours = minutes // 60 # 1 час
- Индексация в двумерных массивах:
Для определения строки по линейному индексу
linear_index = 15 columns = 4 row = linear_index // columns # 3-я строка (индексация с 0)
- Работа с битами и байтами:
Когда нужно разделить большие числа на байты или биты
Целочисленное деление — мощный инструмент, который дополняет стандартное деление и часто используется в связке с операцией получения остатка (%), о которой мы поговорим далее.
Остаток (%)
Оператор получения остатка от деления (%), также известный как оператор модуля, является ключевым инструментом в арсенале Python-разработчика. Он возвращает остаток, который получается после выполнения целочисленного дробления первого операнда на второй. Эта, казалось бы, простая операция, на практике имеет широчайший спектр применений — от проверки четности чисел до создания сложных алгоритмов шифрования.
Как работает % с положительными и отрицательными числами
Для положительных чисел принцип работы оператора % интуитивно понятен:
print(10 % 3) # 1 (10 = 3 * 3 + 1) print(8 % 4) # 0 (8 = 4 * 2 + 0) print(7 % 2) # 1 (7 = 2 * 3 + 1)
Однако при работе с отрицательными числами поведение оператора % может показаться неочевидным:
print(-10 % 3) # 2 (а не -1) print(10 % -3) # -2 (а не 1)
Чтобы понять это поведение, необходимо помнить формулу: a % b = a — (b * (a // b)). Python гарантирует, что знак результата всегда совпадает со знаком делителя (второго операнда), а абсолютное значение результата всегда меньше абсолютного значения делителя.
| Операция | Результат | Объяснение |
|---|---|---|
| 10 % 3 | 1 | 10 = 3 * 3 + 1 |
| -10 % 3 | 2 | -10 = 3 * (-4) + 2 |
| 10 % -3 | -2 | 10 = (-3) * (-4) + (-2) |
| -10 % -3 | -1 | -10 = (-3) * 3 + (-1) |
Практическое применение
Остаток от деления — невероятно полезный инструмент в повседневном программировании. Вот лишь некоторые из распространенных применений:
- Проверка четности числа
def is_even(number): return number % 2 == 0 # True для четных чисел
- Циклическая индексация
Создание бесконечных циклов с возвратом к началу после достижения предела:
# Индексы 0, 1, 2, 3, 0, 1, 2, 3, ... for i in range(10): index = i % 4 print(index, end=' ') # 0 1 2 3 0 1 2 3 0 1
- Форматирование времени
Конвертация секунд в часы, минуты и секунды:
total_seconds = 3665
hours = total_seconds // 3600
minutes = (total_seconds % 3600) // 60
seconds = total_seconds % 60
print(f"{hours}:{minutes}:{seconds}") # 1:1:5
- Алгоритмы шифрования
Многие криптографические алгоритмы используют операцию модуля, например, RSA:
# Упрощенный пример шифрования message = 42 encrypted = (message ** public_key) % n
- Распределение задач
Распределение заданий между исполнителями:
def assign_task(task_id, worker_count): return task_id % worker_count # К какому работнику направить задачу
Хеширование
В реализациях хеш-таблиц для определения индекса в массиве:
def hash_function(key, table_size): return hash(key) % table_size
Проверка делимости
Является ли число кратным другому числу:
def is_divisible(number, divisor): return number % divisor == 0
Паттерны и последовательности
Для создания повторяющихся паттернов в игровой логике или генеративном искусстве.
Оператор получения остатка от деления — это гораздо больше, чем просто способ найти остаток. Это мощный инструмент для решения широкого спектра задач, от базовых проверок четности до сложных алгоритмов. Сочетая его с другими операторами дробления, мы получаем полный арсенал средств для эффективной разработки на Python.
Деление на ноль и как его избежать
В математике деление на ноль неопределено — попытка представить, сколько раз ноль помещается в любом числе, лишена смысла. Python, как язык, придерживающийся математических принципов, обрабатывает такие ситуации соответствующим образом.
Деление и ZeroDivisionError
Когда вы пытаетесь использовать любой из операторов (/, // или %) с нулем в качестве делителя, Python генерирует исключение ZeroDivisionError:
print(10 / 0) # ZeroDivisionError: division by zero print(10 // 0) # ZeroDivisionError: integer division or modulo by zero print(10 % 0) # ZeroDivisionError: integer division or modulo by zero
Такое поведение не является ошибкой в языке — наоборот, это защитный механизм, предотвращающий потенциально опасные ситуации в программе. Неконтролируемое деление на ноль может привести к непредсказуемым результатам или даже сбоям в системах, где важна точность вычислений.
Обработка ошибок (пример try-except)
В реальных приложениях, особенно тех, где данные приходят от пользователя или из внешних источников, важно предусмотреть возможность дробления на ноль. Python предоставляет элегантный способ обработки таких ситуаций через механизм исключений:
def safe_division(numerator, denominator):
try:
result = numerator / denominator
return result
except ZeroDivisionError:
print("Ошибка: деление на ноль невозможно")
return None
# Пример использования
print(safe_division(10, 2)) # 5.0
print(safe_division(10, 0)) # Ошибка: деление на ноль невозможно
# None
Этот подход позволяет программе продолжить выполнение даже при возникновении исключения, вместо аварийного завершения.
Проверка делителя перед операцией (советы)
Альтернативный и часто более эффективный подход — это предварительная проверка делителя перед выполнением операции деления:
def divide_safely(numerator, denominator):
if denominator == 0:
print("Предупреждение: попытка деления на ноль")
return None
return numerator / denominator
Для более сложных сценариев можно комбинировать оба подхода:
def robust_division(a, b, default=None):
if b == 0:
return default
try:
return a / b
except Exception as e:
print(f"Произошла непредвиденная ошибка: {e}")
return default
При выборе подхода к обработке деления на ноль следует руководствоваться контекстом задачи:
- Если деление на ноль — это однозначно ошибка в логике программы, лучше позволить исключению проявиться для быстрого выявления проблемы.
- Если деление на ноль может возникнуть в результате действий пользователя, предпочтительнее использовать проверку или обработку исключений.
- В критических системах часто применяют комбинацию обоих подходов для максимальной надежности.
Грамотная обработка ситуаций деления на ноль — это маркер качественного кода и признак опытного разработчика на Python.
Сокращённая запись операций деления (/=, //=, %=)
В стремлении к элегантному и лаконичному коду Python предлагает сокращенные формы записи для всех операторов деления. Эти операторы объединяют операцию деления и присваивания, что позволяет значительно упростить некоторые распространенные паттерны программирования.
Примеры всех трёх сокращённых операторов
Рассмотрим стандартные и сокращенные формы записи для каждого типа деления:
| Стандартная запись | Сокращённая запись | Описание |
|---|---|---|
| a = a / b | a /= b | Обычное деление с присваиванием |
| a = a // b | a //= b | Целочисленное деление с присваиванием |
| a = a % b | a %= b | Остаток от деления с присваиванием |
На практике это выглядит следующим образом:
# Обычное деление x = 10 x /= 2 print(x) # 5.0 # Целочисленное деление y = 10 y //= 3 print(y) # 3 # Остаток от деления z = 10 z %= 3 print(z) # 1
Сокращенная форма записи не только экономит символы, но и потенциально повышает производительность, так как обращение к переменной происходит только один раз.
Когда это удобно — список ситуаций
Сокращенные операторы особенно полезны в следующих случаях:
- Итеративные алгоритмы Когда значение постепенно изменяется с каждой итерацией:
# Быстрое нахождение наибольшего общего делителя (алгоритм Евклида) def gcd(a, b): while b: a, b = b, a % b return a
- Нормализация данных. Приведение значений к определенному диапазону или шкале:
# Нормализация значений к диапазону [0, 1] for i in range(len(values)): values[i] /= maximum
- Финансовые расчеты Расчет процентов, налогов, скидок:
# Применение налога к стоимости total_price = 100 total_price *= 1.20 # Добавление 20% налога
- Анимации и графика Постепенное изменение координат или размеров:
# Плавное уменьшение размера объекта def shrink_object(): object_size = 100 while object_size > 10: object_size /= 1.1 draw_object(object_size) time.sleep(0.05)
- Обработка циклических значений Работа с углами, временем, координатами в циклических системах:
# Гарантирование, что угол в пределах [0, 360) градусов angle %= 360
- Инкрементальное обновление статистики Когда необходимо постепенно обновлять средние значения или другие статистические показатели:
# Расчет экспоненциального скользящего среднего def update_ema(current_ema, new_value, alpha=0.1): current_ema *= (1 - alpha) current_ema += alpha * new_value return current_ema
Сокращенная запись операторов деления — это не просто синтаксический сахар. Это эффективный инструмент, который делает код более читаемым и менее подверженным ошибкам, особенно в случаях, когда одна и та же переменная участвует в операции и сохраняет результат. Сочетая эти операторы с пониманием нюансов различных типов деления, разработчик может создавать более эффективный и выразительный код на Python.
Частые ошибки при делении и советы
При работе с операторами деления в Python даже опытные разработчики могут сталкиваться с неочевидными ситуациями. Знание типичных ошибок и понимание их причин поможет избежать неприятных сюрпризов в коде.Основные ошибки при делении в Python и способы их предотвращения. Быстрая шпаргалка, которая пригодится в любом проекте.
Основные ошибки при делении в Python и способы их предотвращения. Быстрая шпаргалка, которая пригодится в любом проекте.
Таблица распространенных ошибок и их решений
| Ошибка | Почему возникает | Как избежать |
|---|---|---|
| Неожиданный результат при дроблении отрицательных чисел | Оператор // округляет к отрицательной бесконечности, а не к нулю | Помнить, что -7 // 2 = -4, а не -3. При необходимости использовать int(a/b) для округления к нулю |
| Потеря точности дробных числах | Двоичное представление десятичных дробей часто неточно | Использовать round() или модуль decimal для финансовых расчетов |
| ZeroDivisionError при делении на ноль | Попытка дробления на ноль математически неопределена | Проверять делитель перед операцией или использовать try-except |
| Неверный тип результата | Вы ожидаете int, но получаете float после дробления | Понимать, что оператор / всегда возвращает float. Использовать // для целочисленного деления |
| Неожиданные результаты при использовании % с отрицательными числами | Оператор % следует математическим правилам, а не интуитивным ожиданиям | Знать, что результат a % b имеет знак делителя b. Использовать abs() при необходимости |
| Ошибки при использовании целочисленного дробления для индексации | Оператор // может давать результат на 1 меньше ожидаемого из-за округления вниз | Проверять граничные случаи и учитывать направление округления |
| Непреднамеренное изменение типа при использовании /= | Переменная может изменить тип с int на float | Учитывать, что сокращенные операторы влияют на тип переменной так же, как обычные |
Дополнительные рекомендации
Будьте осторожны с округлением
Если результат деления должен быть целым, но округленным по обычным правилам (а не с отбрасыванием дробной части), используйте round() вместо //:
a = -3.6 print(round(a)) # -4 (округление к ближайшему целому) print(int(a)) # -3 (отбрасывание дробной части) print(a // 1) # -4 (округление вниз)
Проверяйте граничные случаи
Тестируйте операции деления с крайними значениями, особенно с нулем и отрицательными числами.
Документируйте предположения
Если ваш код зависит от определенного поведения операторов деления, явно документируйте это в комментариях или документации.
Используйте правильные типы данных
Для финансовых расчетов и других приложений, требующих точности, используйте decimal.Decimal вместо стандартных float.
Понимание нюансов деления в Python не только помогает избежать ошибок, но и позволяет использовать мощь этих операторов для создания более элегантных и эффективных решений. Помните, что каждый из операторов деления имеет свое специфическое применение, и выбор правильного инструмента для конкретной задачи — ключ к написанию качественного кода.
Заключение
В этой статье мы рассмотрели три ключевых оператора деления в Python: обычное деление (/), целочисленное деление (//) и получение остатка от деления (%). Каждый из них играет важную роль в арсенале Python-разработчика и имеет свои уникальные случаи применения.
Давайте подытожим основные моменты. Понимание нюансов работы с различными типами чисел и операторами деления позволяет:
- Избегать неочевидных ошибок, особенно при работе с отрицательными числами.
- Писать более эффективный и читаемый код с использованием сокращенных операторов (/=, //=, %=).
- Корректно обрабатывать исключительные ситуации, такие как деление на ноль.
- Использовать мощь операторов деления для решения широкого спектра задач — от проверки четности до циклической индексации и шифрования.
Хотите прокачать навыки Python-разработки? Посмотрите подборку курсов по Python — от основ до профессионального уровня!

Операторы в Java: что это, виды и примеры для новичков
Операторы в Java — это не просто знаки «+» и «==». Это инструменты, от которых зависит логика и поведение вашей программы. Разберем, как они устроены, когда их лучше не использовать и какие из них чаще всего приводят к ошибкам.

Как стандарты верстки влияют на успех веб-разработки
Стандарты верстки — это не просто требования, а основа качественного веб-разработки. Узнайте, как правильно применять их на практике и избежать частых ошибок.

Unity в 2025 году: какие технологии и тренды определяют будущее геймдева
ИИ, облачные технологии и гибридно-казуальные игры – ключевые направления развития Unity. Разбираем, как изменится разработка игр и что важно учитывать в новых проектах.

Капча против ботов: гениальное решение или пережиток?
Что такое капча, зачем она нужна, и почему мы всё ещё вынуждены щёлкать по картинкам с автобусами? В статье — ответы, примеры и немного иронии.