Двумерные массивы в Python: что это, как создать и работать с ними

Двумерный массив — это структура данных, которая представляет собой таблицу с строками и столбцами, где каждый элемент имеет два индекса: один для строки, другой для столбца. В математике такие структуры называют матрицами, а в программировании — двумерными массивами или сетками данных.
- Как выглядят массивы и где применяются
- Как работают списки в Python и почему двумерный массив — это список списков
- Способы создания двумерных массивов в Python
- Инициализация двумерных массивов значениями
- Как вводить двумерные массивы от пользователя
- Как вывести двумерный массив
- Доступ к элементам двумерного массива
- Основные операции над двумерными массивами
- Полезные практические примеры
- Заключение
- Рекомендуем посмотреть курсы по Python
Как выглядят массивы и где применяются
В Python двумерные массивы обычно реализуют через список, где каждый элемент внешней структуры содержит вложенную последовательность, представляющую строку таблицы. Давайте разберёмся, как это выглядит на практике:
# Визуальное представление таблицы: # й ц у # к е н # г ш щ # Python-представление: matrix = [['й', 'ц', 'у'], ['к', 'е', 'н'], ['г', 'ш', 'щ']]
Где применяются двумерные массивы? Область их использования весьма обширна:
- Игровые поля — шахматная доска, поле для крестиков-ноликов, карты для стратегий.
- Табличные данные — электронные таблицы, базы данных, расписания.
- Обработка изображений — пиксели изображения можно представить как матрицу значений.
- Графы и сети — матрицы смежности для представления связей между узлами.
- Научные вычисления — математические операции с матрицами, системы уравнений.
- Машинное обучение — представление наборов данных, весовые матрицы нейросетей.
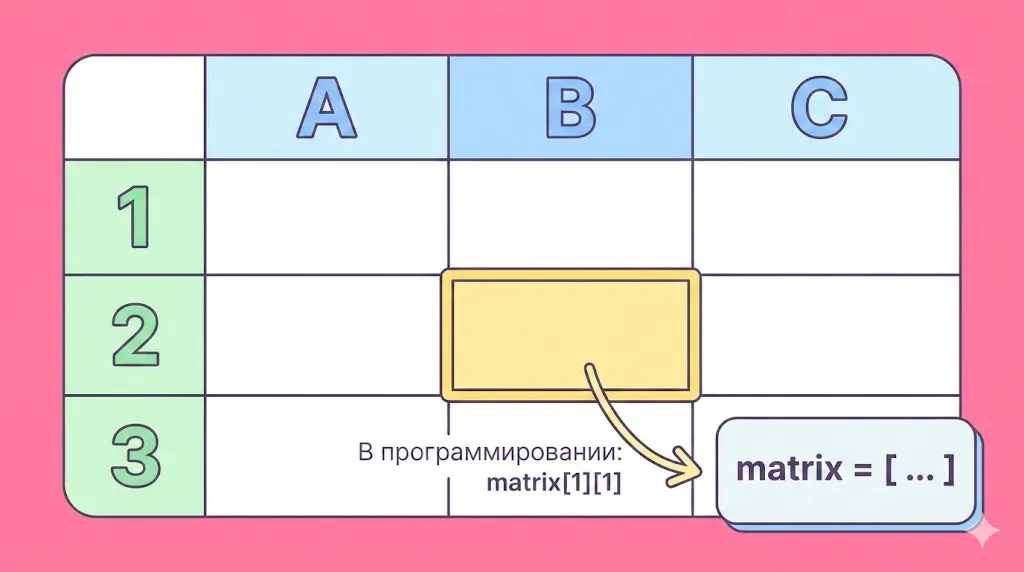
Электронные таблицы — самый простой аналог двумерных массивов. Каждая ячейка имеет свой адрес, который в программировании соответствует индексам строки и столбца.
Рассмотрим простой пример доступа к элементам:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] print(matrix[0][0]) # Выведет 1 (первая строка, первый столбец) print(matrix[2][2]) # Выведет 9 (третья строка, третий столбец) print(matrix[1][0]) # Выведет 4 (вторая строка, первый столбец)
Важное примечание: в Python встроенные списки — это не то же самое, что матрицы из библиотеки NumPy. Такая структура более гибкая (строки могут иметь разную длину), но менее эффективна для математических операций. Для серьёзных вычислений лучше использовать NumPy, но для базовых задач и обучения встроенных списков вполне достаточно.
Как работают списки в Python и почему двумерный массив — это список списков
Чтобы понять устройство двумерных массивов, нужно сначала разобраться с обычными списками. Список в Python — это упорядоченная коллекция элементов, где каждый элемент имеет свой индекс, начиная с нуля. Двумерный массив — это естественное расширение этой концепции: мы создаём список, элементами которого являются другие списки.
Представьте себе книжный шкаф: каждая полка — это строка (внутренний список), а книги на полке — это элементы. Весь шкаф целиком — это двумерный массив.
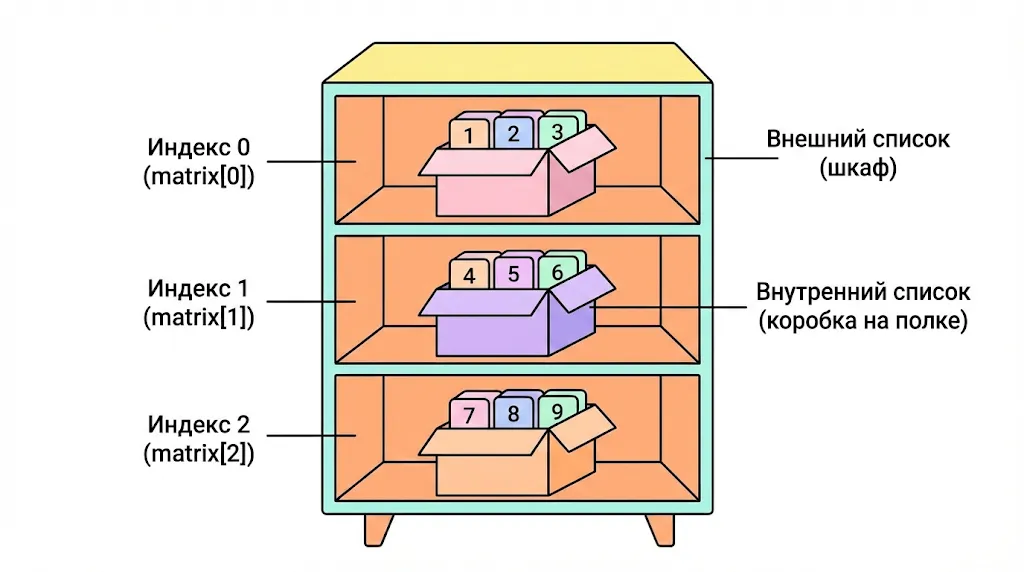
Представьте двумерный массив как книжный шкаф. Сам шкаф — это внешний список, каждая полка — это индекс, а стоящая на ней коробка — это вложенный список, содержащий данные.
Ключевые свойства списков, важные для понимания двумерных массивов:
- Списки могут содержать элементы любого типа, включая другие списки.
- Индексация начинается с нуля.
- Списки изменяемы — можно добавлять, удалять и изменять элементы.
- Длина строк (вложенных списков) может различаться.
Доступ к элементам двумерного массива осуществляется через два индекса:
matrix = [[10, 20, 30], [40, 50, 60], [70, 80, 90]] # Первый индекс -- номер строки, второй -- номер столбца element = matrix[1][2] # Строка 1, столбец 2 → результат: 60 # Можно получить целую строку, используя только первый индекс row = matrix[0] # Получим [10, 20, 30] # Доступ по шагам: temp = matrix[2] # Сначала получаем третью строку: [70, 80, 90] value = temp[1] # Затем второй элемент из неё: 80
Различие между строкой и столбцом:
- Строка — это элемент внешнего списка, доступный напрямую через один индекс: matrix[i].
- Столбец — это набор элементов с одинаковым вторым индексом из разных строк: нужно перебрать все строки и взять элемент с нужным индексом.
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Получить вторую строку -- просто: second_row = matrix[1] # [4, 5, 6] # Получить второй столбец -- нужен цикл: second_column = [matrix[i][1] for i in range(len(matrix))] # [2, 5, 8]
Именно эта асимметрия между строками и столбцами определяет многие особенности работы с двумерными массивами в Python.
Способы создания двумерных массивов в Python
Существует несколько подходов к созданию двумерных массивов, каждый из которых имеет свои преимущества и области применения. Давайте рассмотрим основные методы и разберёмся, когда какой из них стоит использовать.
Ручное создание (список списков)
Самый простой и наглядный способ — явно указать все элементы:
# Создание таблицы 3x3 с буквами matrix = [['а', 'б', 'в'], ['г', 'д', 'е'], ['ж', 'з', 'и']] # Создание таблицы с числами numbers = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
Этот метод применяется, когда:
- Массив небольшой и его содержимое заранее известно.
- Нужна максимальная читаемость кода.
- Данные имеют смысловую структуру (например, игровое поле).
Создание через циклы
Когда размер массива определяется динамически или нужно заполнить его по определённому правилу, используются циклы.
Создание пустой матрицы с заданными размерами:
rows = 3 cols = 4 matrix = [] for i in range(rows): row = [] for j in range(cols): row.append(0) matrix.append(row) print(matrix) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Добавление строк через append:
rows = 3 cols = 3 matrix = [] for i in range(rows): matrix.append([0] * cols) print(matrix) # [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
Генерация данных с вычислениями:
# Создание таблицы умножения size = 5 multiplication_table = [] for i in range(1, size + 1): row = [] for j in range(1, size + 1): row.append(i * j) multiplication_table.append(row) # Результат: # [[1, 2, 3, 4, 5], # [2, 4, 6, 8, 10], # [3, 6, 9, 12, 15], # [4, 8, 12, 16, 20], # [5, 10, 15, 20, 25]]
Создание через генераторы списков
Генераторы списков (list comprehensions) — это наиболее компактный и pythonic способ создания двумерных массивов. Они сочетают создание и заполнение в одну строку.
Базовый синтаксис:
rows = 4 cols = 3 matrix = [[1] * cols for i in range(rows)] print(matrix) # [[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1]]
Упрощённый вариант для одинаковых значений:
rows = 4 cols = 3 matrix = [[1] * cols for i in range(rows)] print(matrix) # [[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1]]
Генерация с вычислениями:
# Матрица, где каждый элемент равен сумме индексов matrix = [[i + j for j in range(4)] for i in range(3)] # Результат: [[0, 1, 2, 3], [1, 2, 3, 4], [2, 3, 4, 5]] # Матрица с произведением индексов matrix = [[i * j for j in range(5)] for i in range(5)]
Распространённая ошибка при создании матриц
Одна из самых частых ошибок начинающих — попытка создать матрицу через умножение списка списков:
# НЕПРАВИЛЬНО! Не делайте так: rows = 3 cols = 4 matrix = [[0] * cols] * rows # Проблема: изменение одной строки изменит все строки matrix[0][0] = 5 print(matrix) # [[5, 0, 0, 0], [5, 0, 0, 0], [5, 0, 0, 0]]
Почему это происходит? Оператор умножения * rows создаёт не копии списка, а несколько ссылок на один и тот же объект в памяти. Все «строки» указывают на один список, поэтому изменение любой из них влияет на остальные.
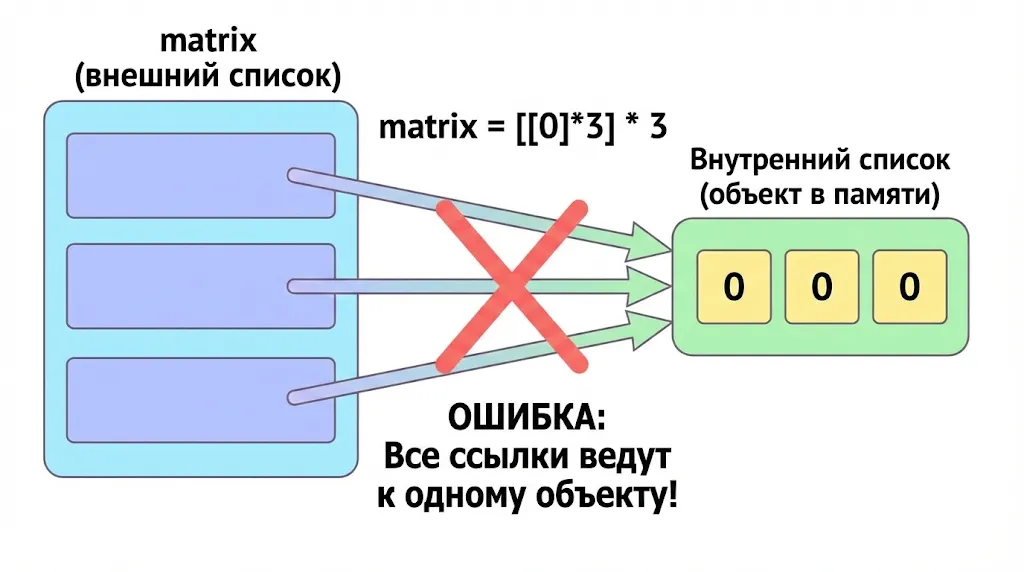
При использовании умножения списков вы создаете не копии, а множество ссылок на один и тот же объект в памяти. Изменение одной «строки» неминуемо приведет к изменению всех остальных.
Правильная альтернатива:
# ПРАВИЛЬНО: rows = 3 cols = 4 matrix = [[0] * cols for _ in range(rows)] # Теперь каждая строка -- отдельный объект matrix[0][0] = 5 print(matrix) # [[5, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Плюсы и минусы различных методов:
- Ручное создание: максимальная наглядность, но неудобно для больших массивов.
- Циклы: понятная логика, хорошо для обучения, но многословно.
- Генераторы: компактность, скорость выполнения, pythonic стиль, но требует привыкания.
Таблица: когда применять каждый метод
| Метод | Когда применять |
|---|---|
| Ручной список | Маленькие массивы с известным содержимым |
| Циклы | Сложная логика заполнения, обучение основам |
| Генераторы | Стандартные задачи, когда нужна компактность |
| [[0]*cols]*rows | НИКОГДА — это ошибка! |
Инициализация двумерных массивов значениями
После создания структуры массива часто требуется заполнить его конкретными значениями. Рассмотрим основные паттерны инициализации, которые встречаются в практической работе.
Заполнение одинаковыми значениями:
Мы уже видели базовый способ заполнения нулями или единицами. Давайте расширим эту идею:
# Матрица из нулей zeros = [[0 for j in range(4)] for i in range(3)] # Матрица из единиц ones = [[1] * 5 for i in range(5)] # Матрица из произвольного значения rows, cols = 4, 3 default_value = 42 matrix = [[default_value] * cols for _ in range(rows)] print(matrix) # [[42, 42, 42], [42, 42, 42], [42, 42, 42], [42, 42, 42]]
Заполнение последовательностью:
Часто нужно создать матрицу с последовательными числами — для тестирования, отладки или решения конкретных задач:
# Последовательное заполнение построчно rows, cols = 3, 4 counter = 1 matrix = [] for i in range(rows): row = [] for j in range(cols): row.append(counter) counter += 1 matrix.append(row) print(matrix) # [[1, 2, 3, 4], # [5, 6, 7, 8], # [9, 10, 11, 12]] # Тот же результат через генератор matrix = [[i * cols + j + 1 for j in range(cols)] for i in range(rows)]
Заполнение случайными числами:
Для тестирования алгоритмов, симуляций и экспериментов часто требуются случайные данные:
import random # Случайные целые числа в диапазоне rows, cols = 4, 5 matrix = [[random.randint(1, 100) for j in range(cols)] for i in range(rows)] # Случайные числа с плавающей точкой matrix_float = [[random.uniform(0, 1) for j in range(cols)] for i in range(rows)] # Случайный выбор из списка значений choices = ['X', 'O', '-'] game_field = [[random.choice(choices) for j in range(3)] for i in range(3)] print(game_field) # Возможный результат: [['X', 'O', '-'], ['O', 'X', 'X'], ['-', 'O', 'X']]
Частые паттерны заполнения:
- Диагональная матрица — единицы на главной диагонали, остальное — нули.
- Шахматный порядок — чередование двух значений.
- Граничное заполнение — особые значения по краям матрицы.
- Заполнение по формуле — значение зависит от позиции элемента.
- Случайное заполнение с ограничениями — например, сумма элементов строки должна равняться определённому значению.
Примеры реализации некоторых паттернов:
# Единичная матрица (диагональная) size = 4 identity = [[1 if i == j else 0 for j in range(size)] for i in range(size)] # [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]] # Шахматный порядок rows, cols = 5, 5 chess = [[1 if (i + j) % 2 == 0 else 0 for j in range(cols)] for i in range(rows)]
Выбор способа инициализации зависит от конкретной задачи: для учебных примеров подойдут простые последовательности, для реальных приложений — случайные или вычисляемые значения, а для научных расчётов часто используются специализированные паттерны вроде диагональных или разреженных матриц.
Как вводить двумерные массивы от пользователя
В реальных программах часто возникает необходимость получить данные двумерного массива от пользователя. Это может быть ввод игрового поля, таблицы результатов или набора данных для обработки. Рассмотрим различные подходы к вводу и обработке возможных ошибок.
Построчный ввод через input()
Классический подход — запросить у пользователя количество строк, а затем построчно считать данные:
# Ввод количества строк
rows = int(input("Введите количество строк: "))
matrix = []
# Построчный ввод
for i in range(rows):
row = list(map(int, input(f"Введите строку {i+1} через пробел: ").split()))
matrix.append(row)
print("Полученный массив:", matrix)
# Пример взаимодействия:
# Введите количество строк: 3
# Введите строку 1 через пробел: 1 2 3
# Введите строку 2 через пробел: 4 5 6
# Введите строку 3 через пробел: 7 8 9
# Полученный массив: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Разберём, что происходит в этом коде:
- input().split() разбивает введённую строку по пробелам.
- map(int, …) преобразует каждый элемент в целое число.
- list() создаёт список из результатов map.
Ввод через генератор списков
Тот же результат можно получить более компактным способом:
rows = int(input("Введите количество строк: "))
matrix = [list(map(int, input().split())) for i in range(rows)]
print(matrix)
Этот вариант короче и элегантнее, но менее нагляден для начинающих. Выбор между развёрнутым и компактным вариантом зависит от приоритетов: читаемость кода или краткость.
Проверка количества элементов
На практике пользователи часто допускают ошибки при вводе: вводят разное количество элементов в строках, используют недопустимые символы или пропускают значения. Давайте добавим базовую проверку:
rows = int(input("Введите количество строк: "))
cols = int(input("Введите количество столбцов: "))
matrix = []
for i in range(rows):
while True:
try:
row = list(map(int, input(f"Строка {i+1} ({cols} чисел): ").split()))
if len(row) != cols:
print(f"Ошибка: нужно ввести ровно {cols} чисел. Попробуйте снова.")
continue
matrix.append(row)
break
except ValueError:
print("Ошибка: введите только целые числа. Попробуйте снова.")
print("Массив успешно создан:", matrix)
Типовые ошибки пользователей при вводе:
- Неверное количество элементов — ввели больше или меньше значений, чем требуется.
- Неправильный тип данных — ввели буквы вместо чисел.
- Лишние пробелы — множественные пробелы между числами (обычно не проблема благодаря split()).
- Пустая строка — нажали Enter без ввода данных.
- Использование запятых вместо пробелов — пользователи иногда вводят «1,2,3» вместо «1 2 3».
Пример обработки запятых как разделителей:
row_input = input("Введите числа (через пробел или запятую): ")
# Заменяем запятые на пробелы, затем разбиваем
row = list(map(int, row_input.replace(',', ' ').split()))
Важно помнить: чем больше проверок вы добавляете, тем надёжнее программа, но тем сложнее становится код. В учебных задачах часто используется упрощённый ввод без проверок, но в реальных приложениях валидация данных критически важна.
Как вывести двумерный массив
После создания или обработки двумерного массива необходимо представить его пользователю в читаемом виде. Python предлагает несколько способов вывода, каждый из которых подходит для разных ситуаций.
Вывод через вложенные циклы
Классический способ — использовать два вложенных цикла для перебора строк и элементов:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] for i in range(len(matrix)): for j in range(len(matrix[i])): print(matrix[i][j], end=' ') print() # Переход на новую строку после каждой строки матрицы # Вывод: # 1 2 3 # 4 5 6 # 7 8 9
Этот подход даёт максимальный контроль: можно легко добавить нумерацию, форматирование или условную логику вывода.
Вывод через обобщённые циклы (for row in matrix)
Более pythonic способ — итерироваться непосредственно по элементам, а не по индексам:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Вывод построчно for row in matrix: for element in row: print(element, end=' ') print() # Альтернативный вариант с выводом целых строк for row in matrix: print(row) # Вывод: # [1, 2, 3] # [4, 5, 6] # [7, 8, 9]
Второй вариант проще, но выводит строки в формате списков Python с квадратными скобками и запятыми, что не всегда удобно для чтения.
Форматированный вывод через join()
Метод join() позволяет создать аккуратный вывод без лишних символов:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for row in matrix:
print(' '.join(map(str, row)))
# Вывод:
# 1 2 3
# 4 5 6
# 7 8 9
Здесь map(str, row) преобразует все числа в строки, а ‘ ‘.join() объединяет их через пробел. Можно использовать другой разделитель:
# Вывод с табуляцией (удобно для широких чисел)
for row in matrix:
print('\t'.join(map(str, row)))
# Вывод в формате CSV
for row in matrix:
print(','.join(map(str, row)))
Как вывести только строку или только столбец
Иногда требуется вывести не весь массив, а конкретную строку или столбец.
Вывод конкретной строки:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
# Вывести вторую строку (индекс 1)
row_index = 1
for element in matrix[row_index]:
print(element, end=' ')
print()
# Или проще:
print(' '.join(map(str, matrix[row_index])))
# Вывод: 4 5 6
Вывод конкретного столбца:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
# Вывести второй столбец (индекс 1)
col_index = 1
for row in matrix:
print(row[col_index], end=' ')
print()
# Или через генератор списков:
column = [row[col_index] for row in matrix]
print(' '.join(map(str, column)))
# Вывод: 2 5 8
Обратите внимание на асимметрию: получить строку просто (matrix[row_index]), а для столбца нужно перебирать все строки. Это прямое следствие того, что Python хранит двумерные массивы как списки строк, а не универсальную матричную структуру.
Выбор метода вывода зависит от контекста: для отладки подойдёт простой print(matrix), для пользовательского интерфейса — форматированный вывод через join(), а для специфичных задач — циклы с дополнительной логикой.
Доступ к элементам двумерного массива
Понимание системы индексации — ключ к эффективной работе с двумерными массивами. Давайте разберёмся, как обращаться к различным элементам и структурам внутри матрицы.
Базовая индексация [i][j]:
Доступ к элементу осуществляется через два индекса: первый указывает на строку, второй — на столбец. Важно помнить, что нумерация начинается с нуля:
matrix = [[10, 20, 30], [40, 50, 60], [70, 80, 90]] # Первый элемент первой строки print(matrix[0][0]) # 10 # Последний элемент последней строки print(matrix[2][2]) # 90 # Элемент из второй строки, третьего столбца print(matrix[1][2]) # 60
Объяснение структуры индексов:
Можно представить доступ к элементу как двухэтапный процесс:
- matrix[i] — получаем строку с индексом i (это список)
- [j] — из этой строки берём элемент с индексом j
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Двухэтапный доступ row = matrix[1] # Получаем [4, 5, 6] element = row[2] # Получаем 6 # Эквивалентно одному выражению element = matrix[1][2] # 6
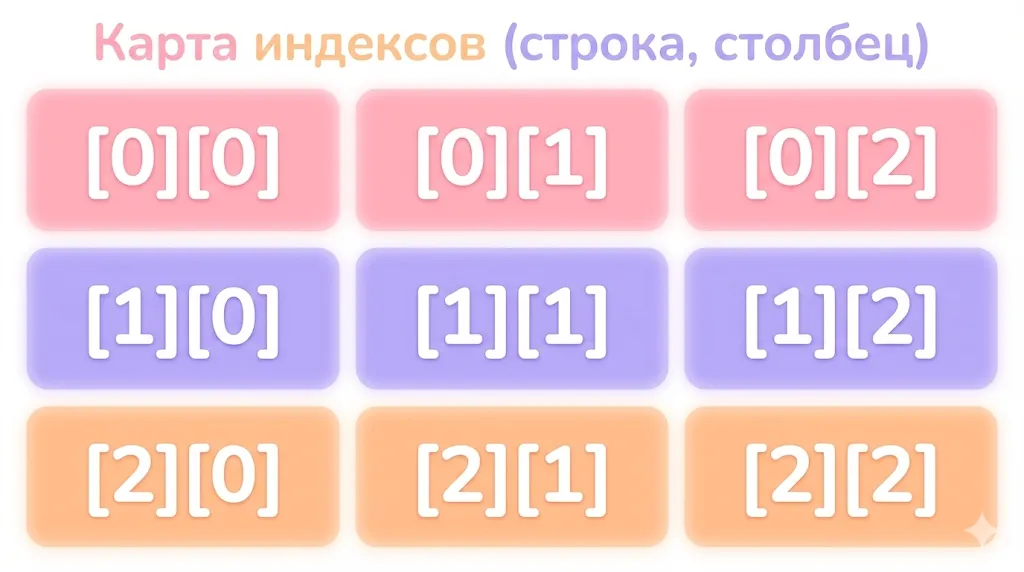
Эта схема помогает запомнить порядок индексов: сначала указывается номер строки, затем номер столбца. Помните, что в Python нумерация начинается с нуля.
Работа с границами матрицы:
Выход за пределы массива вызывает ошибку IndexError. Чтобы избежать этого, нужно проверять границы:
matrix = [[1, 2, 3], [4, 5, 6]]
rows = len(matrix) # Количество строк: 2
cols = len(matrix[0]) # Количество столбцов: 3
# Безопасный доступ с проверкой
i, j = 1, 2
if 0 <= i < rows and 0 <= j < cols:
print(matrix[i][j]) # 6
else:
print("Индекс вне границ")
# Использование отрицательных индексов
print(matrix[-1][-1]) # 6 (последний элемент последней строки)
print(matrix[-2][-3]) # 1 (первый элемент первой строки, считая с конца)
Получение строки и столбца:
matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]] # Получить целую строку second_row = matrix[1] # [5, 6, 7, 8] # Получить столбец (требует перебора) third_column = [row[2] for row in matrix] # [3, 7, 11] # Получить диагональ (главную) main_diagonal = [matrix[i][i] for i in range(min(len(matrix), len(matrix[0])))] # [1, 6, 11]
Варианты доступа к элементам:
- Прямой доступ — matrix[i][j] для конкретного элемента.
- Доступ к строке — matrix[i] возвращает список.
- Доступ к столбцу — требует генератора или цикла.
- Срезы строки — matrix[i][start:end] для части строки.
- Отрицательные индексы — доступ с конца массива.
Мини-таблица: типы доступа
| Операция | Синтаксис | Результат |
|---|---|---|
| Элемент | matrix[1][2] | Одно значение |
| Строка | matrix[1] | Список (строка) |
| Столбец | [row[2] for row in matrix] | Список (столбец) |
| Часть строки | matrix[1][0:2] | Срез списка |
| Диагональ | [matrix[i][i] for i in range(n)] | Список значений |
Важно помнить: при работе с элементами двумерного массива всегда учитывайте возможность выхода за границы, особенно если индексы вычисляются динамически или зависят от пользовательского ввода.
Основные операции над двумерными массивами
Работа с двумерными массивами не ограничивается созданием и выводом — в реальных задачах требуется выполнять различные операции: поиск, сортировку, вычисления и модификацию данных. Рассмотрим наиболее распространённые операции.
Обход и перебор
Базовая операция — перебор всех элементов массива для их обработки или анализа:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
# Классический обход с индексами
for i in range(len(matrix)):
for j in range(len(matrix[i])):
print(f"Элемент [{i}][{j}] = {matrix[i][j]}")
# Обход без индексов
for row in matrix:
for element in row:
print(element, end=' ')
print()
# Получение всех элементов в один список
all_elements = [element for row in matrix for element in row]
print(all_elements) # [1, 2, 3, 4, 5, 6, 7, 8, 9]
Поиск значений
Часто требуется найти максимальное, минимальное значение или проверить наличие конкретного элемента:
matrix = [[15, 3, 8], [21, 5, 12], [9, 18, 6]]
# Поиск максимума
max_value = matrix[0][0]
max_position = (0, 0)
for i in range(len(matrix)):
for j in range(len(matrix[i])):
if matrix[i][j] > max_value:
max_value = matrix[i][j]
max_position = (i, j)
print(f"Максимум: {max_value} в позиции {max_position}") # Максимум: 21 в позиции (1, 0)
# Поиск минимума через генератор
all_elements = [element for row in matrix for element in row]
min_value = min(all_elements)
print(f"Минимум: {min_value}") # Минимум: 3
# Поиск конкретного элемента
target = 12
found = False
for i in range(len(matrix)):
for j in range(len(matrix[i])):
if matrix[i][j] == target:
print(f"Найдено {target} в позиции [{i}][{j}]")
found = True
break
if found:
break
Суммирование элементов
Вычисление сумм — частая задача при анализе данных:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
# Сумма всей матрицы
total_sum = sum(sum(row) for row in matrix)
print(f"Общая сумма: {total_sum}") # 45
# Сумма конкретной строки
row_index = 1
row_sum = sum(matrix[row_index])
print(f"Сумма строки {row_index}: {row_sum}") # 15
# Сумма конкретного столбца
col_index = 2
col_sum = sum(row[col_index] for row in matrix)
print(f"Сумма столбца {col_index}: {col_sum}") # 18
# Суммы всех строк
row_sums = [sum(row) for row in matrix]
print(f"Суммы строк: {row_sums}") # [6, 15, 24]
# Суммы всех столбцов
col_count = len(matrix[0])
col_sums = [sum(row[j] for row in matrix) for j in range(col_count)]
print(f"Суммы столбцов: {col_sums}") # [12, 15, 18]
Сортировка
Сортировка двумерных массивов может выполняться по-разному в зависимости от задачи:
matrix = [[5, 2, 8], [1, 9, 3], [6, 4, 7]] # Сортировка каждой строки отдельно sorted_rows = [sorted(row) for row in matrix] print(sorted_rows) # [[2, 5, 8], [1, 3, 9], [4, 6, 7]] # Сортировка с изменением исходного массива for row in matrix: row.sort() print(matrix) # [[2, 5, 8], [1, 3, 9], [4, 6, 7]] # Полная сортировка: собрать все элементы, отсортировать, разбить обратно matrix = [[5, 2, 8], [1, 9, 3], [6, 4, 7]] rows = len(matrix) cols = len(matrix[0]) # Собираем все элементы all_elements = [element for row in matrix for element in row] all_elements.sort() # Разбиваем обратно на строки sorted_matrix = [] for i in range(rows): row = all_elements[i * cols : (i + 1) * cols] sorted_matrix.append(row) print(sorted_matrix) # [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Изменение и удаление элементов
Двумерные массивы в Python изменяемы, что позволяет модифицировать их содержимое:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Заменить значение matrix[1][1] = 50 print(matrix) # [[1, 2, 3], [4, 50, 6], [7, 8, 9]] # Удалить строку del matrix[0] print(matrix) # [[4, 50, 6], [7, 8, 9]] # Удалить элемент из строки (нарушает прямоугольность матрицы!) matrix[0].pop(1) print(matrix) # [[4, 6], [7, 8, 9]] # Добавить новую строку matrix.append([10, 11, 12]) print(matrix) # [[4, 6], [7, 8, 9], [10, 11, 12]] # Заменить все элементы, удовлетворяющие условию matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] for i in range(len(matrix)): for j in range(len(matrix[i])): if matrix[i][j] % 2 == 0: # Чётные числа matrix[i][j] = 0 print(matrix) # [[1, 0, 3], [0, 5, 0], [7, 0, 9]]
Пошаговая инструкция для типовых операций:
- Найти максимум: перебрать все элементы, сравнивая с текущим максимумом.
- Посчитать сумму: использовать вложенные sum() или цикл с накоплением.
- Отсортировать строки: применить sorted() или .sort() к каждой строке.
- Изменить элементы: обратиться по индексу и присвоить новое значение.
- Удалить строку: использовать del matrix[i] или matrix.pop(i).
- Отфильтровать значения: создать новую матрицу через генератор с условием.
Эти операции составляют основу работы с двумерными массивами и применяются в самых разных задачах — от анализа данных до реализации игровой логики.
Полезные практические примеры
Теория становится понятнее, когда мы видим её применение на конкретных задачах. Рассмотрим несколько практических примеров, которые часто встречаются в реальной работе с двумерными массивами.
Транспонирование матрицы:
Транспонирование — это операция, при которой строки и столбцы меняются местами. Элемент matrix[i][j] становится элементом transposed[j][i]:
matrix = [[1, 2, 3], [4, 5, 6]] # Транспонирование через генератор списков rows = len(matrix) cols = len(matrix[0]) transposed = [[matrix[i][j] for i in range(rows)] for j in range(cols)] print(transposed) # [[1, 4], # [2, 5], # [3, 6]] # Альтернативный способ через встроенную функцию zip transposed2 = [list(row) for row in zip(*matrix)] print(transposed2) # Тот же результат
Разворот строк и столбцов:
Иногда требуется отразить матрицу по горизонтали или вертикали:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Разворот строк (зеркало по горизонтали) reversed_rows = matrix[::-1] print(reversed_rows) # [[7, 8, 9], # [4, 5, 6], # [1, 2, 3]] # Разворот столбцов (зеркало по вертикали) reversed_cols = [row[::-1] for row in matrix] print(reversed_cols) # [[3, 2, 1], # [6, 5, 4], # [9, 8, 7]] # Поворот на 90 градусов по часовой стрелке rotated = [[matrix[rows-1-j][i] for j in range(rows)] for i in range(cols)]
Подсчёт элементов по условию:
Часто нужно посчитать, сколько элементов удовлетворяют определённому условию:
matrix = [[12, 5, 18, 3],
[7, 21, 9, 14],
[6, 11, 25, 8]]
# Подсчёт чётных чисел
even_count = sum(1 for row in matrix for element in row if element % 2 == 0)
print(f"Чётных чисел: {even_count}") # 6
# Подсчёт элементов больше 10
above_ten = sum(1 for row in matrix for element in row if element > 10)
print(f"Элементов больше 10: {above_ten}") # 5
# Подсчёт элементов в каждой строке по условию
counts_per_row = [sum(1 for element in row if element > 10) for row in matrix]
print(f"В каждой строке: {counts_per_row}") # [2, 2, 1]
Нахождение среднего значения по строкам:
Практическая задача анализа данных — вычислить среднее значение для каждой строки:
matrix = [[10, 20, 30, 40],
[15, 25, 35, 45],
[5, 15, 25, 35]]
# Среднее по каждой строке
averages = [sum(row) / len(row) for row in matrix]
print(f"Средние значения: {averages}") # [25.0, 30.0, 20.0]
# Среднее по каждому столбцу
cols = len(matrix[0])
col_averages = [sum(row[j] for row in matrix) / len(matrix) for j in range(cols)]
print(f"Средние по столбцам: {col_averages}") # [10.0, 20.0, 30.0, 40.0]
# Общее среднее по всей матрице
total_avg = sum(sum(row) for row in matrix) / sum(len(row) for row in matrix)
print(f"Общее среднее: {total_avg}") # 25.0
Поиск седловой точки:
Седловая точка — элемент, который является минимумом в своей строке и максимумом в своём столбце (или наоборот):
matrix = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
# Поиск седловой точки (минимум в строке, максимум в столбце)
for i in range(len(matrix)):
for j in range(len(matrix[i])):
element = matrix[i][j]
# Проверяем: минимум в строке?
if element == min(matrix[i]):
# Проверяем: максимум в столбце?
column = [row[j] for row in matrix]
if element == max(column):
print(f"Седловая точка: {element} в позиции [{i}][{j}]")
Создание матрицы расстояний:
Представим задачу: есть список координат точек, нужно построить матрицу расстояний между ними:
import math
points = [(0, 0), (3, 4), (6, 8)]
# Создаём матрицу расстояний
n = len(points)
distance_matrix = [[0.0] * n for _ in range(n)]
for i in range(n):
for j in range(n):
x1, y1 = points[i]
x2, y2 = points[j]
distance = math.sqrt((x2 - x1)**2 + (y2 - y1)**2)
distance_matrix[i][j] = round(distance, 2)
# Вывод матрицы
for row in distance_matrix:
print([f"{x:6.2f}" for x in row])
# [ 0.00 5.00 10.00]
# [ 5.00 0.00 5.00]
# [ 10.00 5.00 0.00]
Список типовых задач для практики:
- Найти сумму элементов на главной и побочной диагоналях
- Определить, является ли матрица симметричной
- Найти строку с максимальной суммой элементов
- Заполнить матрицу по спирали
- Проверить, содержит ли она дубликаты
- Найти все локальные максимумы (элементы больше всех соседей)
- Создать матрицу смежности для графа
Эти примеры демонстрируют, что двумерные массивы — это не просто абстрактная структура данных, а практический инструмент для решения реальных задач: от обработки табличных данных до реализации алгоритмов на графах и матрицах.
Заключение
Мы разобрали основы работы с двумерными массивами в Python — от базовых концепций до практических примеров применения. Теперь вы должны уметь создавать матрицы различными способами, заполнять их данными, выводить в удобном формате и выполнять типовые операции: поиск, сортировку, суммирование и модификацию элементов. Подведем итоги:
- Двумерный массив в python — это список списков. Такая структура позволяет хранить данные в виде строк и столбцов.
- Создать матрицу можно вручную, через циклы или генераторы списков. Выбор способа зависит от задачи и объёма данных.
- Важно избегать ошибки с умножением списков. Иначе все строки будут ссылаться на один и тот же объект.
- Доступ к элементам осуществляется через два индекса. Строки получать проще, чем столбцы.
Если вы только начинаете осваивать профессию python-разработчик, рекомендуем обратить внимание на подборку курсов по python. В программах есть теоретическая и практическая часть, чтобы вы могли закрепить навыки работы с массивами на реальных примерах.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
скоро
|
Подробнее |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 марта
|
Подробнее |
|
Fullstack-разработчик на Python
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
175 800 ₽
308 367 ₽
|
От
5 139 ₽/мес
|
Длительность
18 месяцев
|
Старт
29 января
|
Подробнее |
|
Python-разработчик
|
Академия Синергия
35 отзывов
|
Цена
с промокодом KURSHUB
91 560 ₽
228 900 ₽
|
От
3 179 ₽/мес
4 552 ₽/мес
|
Длительность
6 месяцев
|
Старт
3 февраля
|
Подробнее |
|
Профессия Python-разработчик
|
Skillbox
218 отзывов
|
Цена
Ещё -20% по промокоду
74 507 ₽
149 015 ₽
|
От
6 209 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
30 января
|
Подробнее |

Maven: как ускорить разработку и избежать ошибок?
Если вы хотите автоматизировать сборку Java-проектов и тратить меньше времени на рутину, познакомьтесь с Maven – инструментом, который меняет подход к разработке.

Профессии, где нужна математика: полное руководство
Если вы рассматриваете профессии, связанные с математикой, и хотите понять, куда двигаться дальше, этот материал поможет разобраться в нюансах рынка. Какие навыки реально нужны? Что выбрать новичку? Разберёмся простым языком и без лишней теории.

Лучшие панели управления хостингом и бесплатные альтернативы cPanel в 2025 году
Если ищете удобные панели управления хостингом 2025 и не знаете, с чего начать, этот материал поможет разобраться. Какие функции действительно важны, на что смотреть при выборе и почему одни решения удобнее других? Разберём всё простым языком и без лишних терминов.

Почему классическая терапия не работает — и что делать
Что такое схема-терапия и почему её сравнивают с «рефакторингом психики»? Рассказываем, как она помогает справиться с детскими травмами и глубинными установками.