Метод главных компонент (PCA): что это, как работает и зачем он нужен
В эпоху больших данных мы сталкиваемся с парадоксом: чем больше информации мы собираем, тем сложнее её анализировать. Представьте, что вам нужно изучить характеристики автомобилей, учитывая сотни параметров — от мощности двигателя до цвета обивки салона. Как найти действительно важные закономерности в этом информационном хаосе?
Метод главных компонент (Principal Component Analysis, PCA) — это математический инструмент, который помогает выделить самое важное из массива данных, отбросив шум и избыточность. По сути, PCA находит скрытые закономерности в данных и создаёт упрощённую модель, сохраняющую максимум полезной информации при минимуме переменных.
Зачем это нужно? Снижение размерности данных решает сразу несколько задач: ускоряет обработку информации, делает возможной визуализацию сложных данных и помогает выявить неочевидные связи между параметрами. В дальнейших разделах мы разберём математику метода, рассмотрим алгоритм работы и покажем практические примеры применения МГП в различных сферах.
- Когда и зачем применять метод главных компонент
- Как работает метод главных компонент
- Как выбрать количество главных компонент
- Модификации метода
- Ограничения и подводные камни
- Пример использования на реальных данных
- Чем МГП отличается от факторного анализа?
- Альтернативы: когда нужны другие методы
- Заключение
- Рекомендуем посмотреть курсы по системной аналитике
Когда и зачем применять метод главных компонент
Метод главных компонент решает три ключевые задачи современного анализа данных. Во-первых, снижение размерности — когда у нас есть десятки или сотни взаимосвязанных параметров, PCA помогает выделить наиболее информативные комбинации. Во-вторых, визуализация многомерных данных — проецируя сложные наборы на плоскость, мы можем увидеть структуру данных глазами. В-третьих, шумоподавление — метод естественным образом фильтрует случайные флуктуации, сохраняя основные тенденции.
В бизнесе МГП активно применяется в финансовом анализе для оценки рисков портфелей, в маркетинге — для сегментации клиентов по поведенческим паттернам, в производстве — для контроля качества продукции. Научные исследования используют метод в биоинформатике для анализа генетических данных, в нейронауке — для обработки сигналов мозга, в климатологии — для выявления долгосрочных трендов.
Когда подходит:
- Данные имеют линейные зависимости.
- Переменные коррелируют между собой.
- Нужна быстрая предобработка для машинного обучения.
- Требуется визуализация высокомерных данных.
Когда не стоит применять:
- Данные содержат важные нелинейные зависимости.
- Интерпретируемость исходных признаков критичана.
- Данные дискретные или категориальны.
- Шум в данных имеет структурированный характер МГП.
Важно понимать: МГП — не универсальное решение, а специализированный инструмент для конкретного класса задач.
Как работает метод главных компонент
Представим, что наши данные — это облако точек в многомерном пространстве. PCA ищет такие направления в этом пространстве, вдоль которых данные «растянуты» максимально сильно. Эти направления и называются главными компонентами — новыми осями координат, которые лучше всего описывают структуру наших данных.
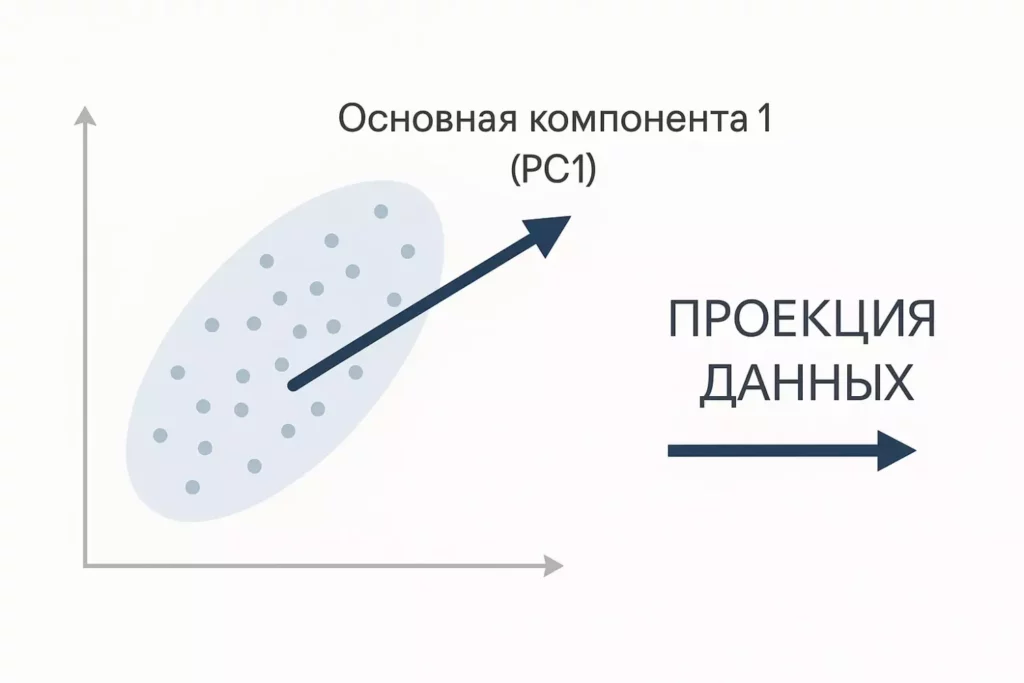
PCA находит направление максимальной вариативности (PC1) и проектирует на него данные — это и есть первая главная компонента.
Общая идея метода заключается в замене исходных признаков на новые ортогональные оси. Если исходные переменные могли быть взаимосвязаны (например, объём двигателя и расход топлива), то главные компоненты всегда независимы друг от друга. Первая главная компонента содержит максимальную долю информации о различиях в данных, вторая — максимум из оставшейся вариативности, и так далее.
Математическую основу составляет ковариационная матрица — она описывает, как переменные связаны между собой. Из этой матрицы мы извлекаем собственные векторы и собственные значения. Собственные векторы указывают направления главных компонент, а собственные значения показывают, сколько информации содержится в каждом направлении.
Альтернативный подход использует сингулярное разложение (SVD) исходной матрицы данных. С математической точки зрения это даёт тот же результат, но часто работает быстрее и численно стабильнее, особенно для больших наборов данных.
| Шаг | Описание | Зачем нужно |
|---|---|---|
| 1. Центрирование | Вычитаем среднее значение из каждой переменной | Убираем смещение, фокусируемся на вариативности |
| 2. Ковариационная матрица | Вычисляем связи между переменными | Понимаем структуру зависимостей |
| 3. Собственные векторы | Находим направления максимальной дисперсии | Определяем новые оси координат |
| 4. Сортировка | Упорядочиваем компоненты по значимости | Выбираем наиболее информативные направления |
| 5. Проекция | Переводим данные в новую систему координат | Получаем упрощённое представление |
Ключевое преимущество МГП — его способность автоматически выявлять скрытые закономерности в данных, которые не всегда очевидны при анализе исходных переменных.
Пошаговый алгоритм PCA
Разберём детально каждый этап применения метода главных компонент, чтобы понять, что происходит «под капотом» алгоритма.
- Центрирование и нормализация данных. Первый шаг — приведение всех переменных к единому масштабу. Мы вычитаем из каждого значения среднее по соответствующей переменной, получая данные с нулевым средним. Если переменные измеряются в разных единицах (например, возраст в годах и доход в рублях), обязательно применяем стандартизацию — делим на стандартное отклонение.
- Построение ковариационной матрицы. Вычисляем матрицу, которая показывает, как связаны между собой все пары переменных. Диагональные элементы содержат дисперсии отдельных переменных, а остальные — ковариации между парами. Эта матрица описывает «форму» нашего облака данных в многомерном пространстве.
- Нахождение собственных векторов и значений. Решаем характеристическое уравнение для ковариационной матрицы. Собственные векторы показывают направления главных компонент, а собственные значения — насколько важна каждая компонента. В современных реализациях часто используется SVD-разложение как более численно стабильная альтернатива.
- Выбор количества компонент. Анализируем долю объяснённой дисперсии для каждой компоненты. Обычно оставляем столько компонент, чтобы сохранить 80-95% исходной информации. Этот выбор — компромисс между простотой модели и полнотой описания данных.
- Построение новых признаков. Проецируем исходные данные на выбранные главные компоненты, умножая центрированную матрицу данных на матрицу собственных векторов. Результат — новый набор данных в пространстве меньшей размерности, где каждая переменная представляет собой линейную комбинацию исходных признаков.
Как выбрать количество главных компонент
Один из самых важных практических вопросов при применении PCA — сколько компонент оставить? Слишком много компонент сводят на нет преимущества метода, слишком мало — теряют критически важную информацию.
Метод «сломанной трости» (scree plot) предлагает строить график собственных значений и искать «излом» — точку, где значения резко уменьшаются. Визуально это напоминает согнутую палку, отсюда и название. Компоненты до излома считаются значимыми, после — шумом.
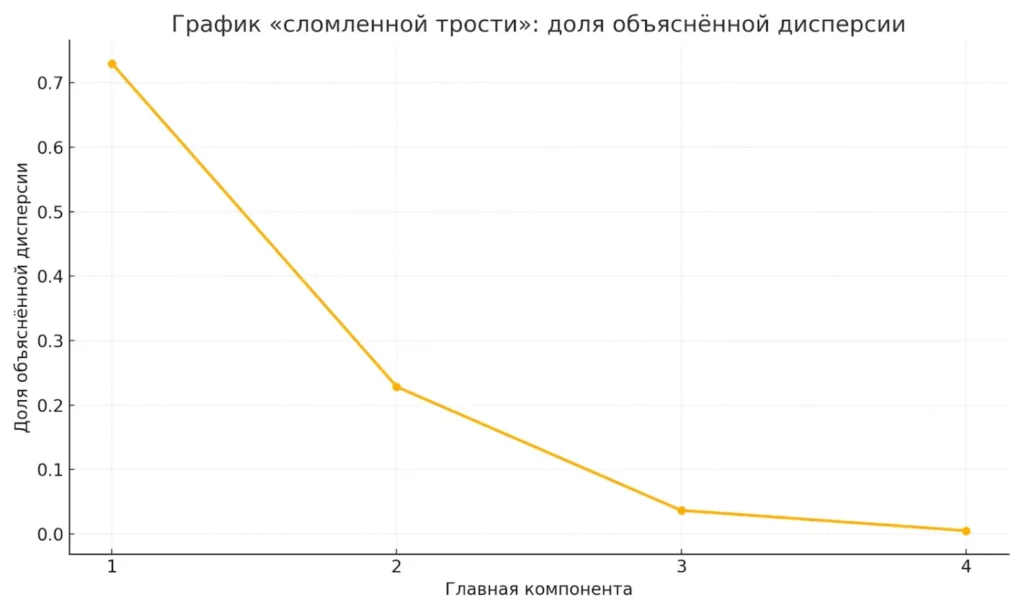
График показывает, какую долю дисперсии объясняет каждая главная компонента. Помогает определить оптимальное количество компонент для анализа.
Критерий Кайзера рекомендует оставлять только те компоненты, собственные значения которых больше единицы (для стандартизированных данных). Логика проста: компонента должна объяснять больше вариативности, чем одна исходная переменная.
Анализ доли объяснённой дисперсии — наиболее популярный подход. Мы вычисляем, какой процент общей вариативности данных сохраняет каждая компонента. Стандартные пороги: 80% для разведочного анализа, 90-95% для серьёзных исследований.
Что происходит при неправильном выборе? Слишком много компонент приводят к переобучению — модель запоминает шум вместо закономерностей. Слишком мало компонент могут пропустить важные паттерны в данных, особенно если они проявляются в последующих компонентах.
На практике мы рекомендуем использовать комбинацию методов: сначала построить scree plot для визуальной оценки, затем проверить критерий накопленной дисперсии. Финальное решение часто зависит от конкретной задачи — для визуализации достаточно 2-3 компонент, для предобработки данных может потребоваться больше.
Модификации метода
Классический — лишь начало семейства методов снижения размерности. Развитие вычислительных технологий и понимание ограничений стандартного подхода привели к созданию специализированных модификаций для решения конкретных задач.
Тензорный расширяет метод на многомерные массивы данных. Если классический PCA работает с двумерными матрицами, то тензорная версия обрабатывает данные произвольной размерности — например, временные ряды изображений или многоканальные сигналы. Это особенно актуально в компьютерном зрении и обработке видео.
Робастный учитывает наличие выбросов в данных. Стандартный метод чувствителен к аномальным значениям, которые могут исказить направления главных компонент. Робастная версия разделяет данные на низкоранговую матрицу (основной сигнал) и разреженную матрицу (выбросы), что критично для анализа данных с измерительными ошибками.
Kernel решает проблему нелинейных зависимостей. Метод неявно переводит данные в пространство более высокой размерности с помощью ядерных функций, где нелинейные связи становятся линейными. Затем применяется обычный PCA. Популярные ядра: полиномиальное, радиальное (RBF), сигмоидное.
Интересно сравнить МГП с автоэнкодерами — нейросетевой альтернативой. Линейный автоэнкодер математически эквивалентен PCA, но нелинейные версии могут выявлять более сложные паттерны. Однако они требуют больше вычислительных ресурсов и менее интерпретируемы.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Классический | Простота, интерпретируемость | Только линейные зависимости |
| Kernel | Учёт нелинейностей | Сложность выбора ядра |
| Робастный | Устойчивость к выбросам | Вычислительная сложность |
Выбор конкретной модификации зависит от природы данных и решаемой задачи.
Ограничения и подводные камни
Несмотря на популярность и элегантность, метод главных компонент имеет существенные ограничения, которые важно понимать перед применением.
- Чувствительность к масштабированию — основная проблема практического использования. Если одна переменная измеряется в рублях (миллионы), а другая в процентах (0-100), то первая автоматически получит больший вес при построении компонент. Решение кажется очевидным — стандартизация, но здесь возникает дилемма: нормализация может «уравнять» действительно важные и второстепенные переменные.
- Игнорирование нелинейных зависимостей ограничивает применимость метода в реальных задачах. PCA ищет только линейные комбинации переменных, пропуская сложные взаимосвязи. Классический пример — данные в форме подковы или спирали, где основная структура нелинейна, но МГП этого не увидит.
- Потеря интерпретируемости создаёт проблемы в бизнес-приложениях. Главные компоненты представляют собой абстрактные комбинации исходных переменных, которые сложно объяснить заказчику или регулятору. Если исходные признаки имели понятный смысл (возраст, доход, стаж), то «первая главная компонента» — это математическая абстракция.
Важно помнить: PCA может давать обманчивые результаты при работе с категориальными данными, временными рядами с трендом или данными с пропущенными значениями.
Показательный пример неудачного применения — попытка применить PCA к данным классификации, где классы расположены концентрическими окружностями. Первые главные компоненты будут описывать общее расположение точек, полностью игнорируя границы между классами. В результате снижение размерности сделает классификацию невозможной, хотя в исходном пространстве задача решается легко.
Перед применением МГП стоит задать себе вопрос: действительно ли наши данные имеют линейную структуру, и готовы ли мы пожертвовать интерпретируемостью ради упрощения?
Пример использования на реальных данных
Рассмотрим практическое применение метода на классическом наборе данных Iris — характеристиках цветков ириса. Этот пример демонстрирует весь процесс от подготовки данных до интерпретации результатов.
Подготовка данных и импорт библиотек:
import numpy as np import pandas as pd from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler from sklearn.datasets import load_iris import matplotlib.pyplot as plt # Загружаем данные iris = load_iris() data = pd.DataFrame(iris.data, columns=iris.feature_names) target = iris.target
Стандартизация — критически важный шаг:
scaler = StandardScaler() data_scaled = scaler.fit_transform(data)
Исходные данные содержат четыре признака: длину и ширину лепестков, длину и ширину чашелистиков. Измерения проводились в сантиметрах, но диапазоны значений различаются, поэтому стандартизация обязательна.
Применение и анализ результатов:
# Создаем модель PCA
pca = PCA()
data_pca = pca.fit_transform(data_scaled)
# Анализируем объясненную дисперсию
explained_variance = pca.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_variance)
print("Доля объясненной дисперсии по компонентам:")
for i, ratio in enumerate(explained_variance):
print(f"PC{i+1}: {ratio:.3f} ({ratio*100:.1f}%)")
Результаты показывают:
- PC1: 0.729 (72.9%) — основная компонента.
- PC2: 0.229 (22.9%) — вторая по важности.
- Вместе первые две компоненты объясняют 95.8% вариативности.
Визуализация результатов:
plt.figure(figsize=(10, 8))
colors = ['red', 'green', 'blue']
target_names = iris.target_names
for target_value, color, name in zip([0, 1, 2], colors, target_names):
indices = target == target_value
plt.scatter(data_pca[indices, 0], data_pca[indices, 1],
c=color, label=name, alpha=0.7)
plt.xlabel(f'PC1 ({explained_variance[0]*100:.1f}% variance)')
plt.ylabel(f'PC2 ({explained_variance[1]*100:.1f}% variance)')
plt.title('PCA: Iris Dataset Projection')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
График показывает отличное разделение трёх видов ирисов в пространстве главных компонент. Особенно хорошо отделяется Iris-setosa, а два других вида частично пересекаются — что соответствует биологической реальности.
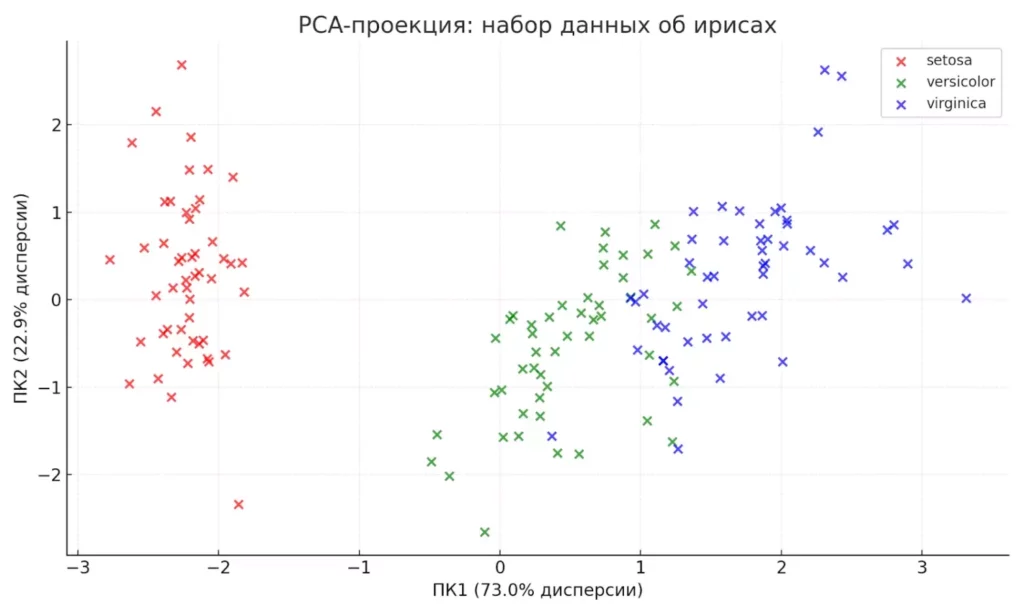
Данные ирисов после снижения размерности с 4 до 2 компонент. Хорошо видно, как метод разделяет три вида цветков.
Этот пример демонстрирует ключевые преимущества PCA: снижение размерности с 4 до 2 переменных при сохранении 95% информации и получение наглядной визуализации сложных биологических данных.
Чем МГП отличается от факторного анализа?
Метод главных компонент часто путают с факторным анализом — действительно, оба метода работают с корреляционными структурами данных и снижают размерность. Однако их цели и математический аппарат принципиально различаются.
Цель МГП — максимально точно воспроизвести исходную дисперсию данных с помощью меньшего числа переменных. Метод не делает предположений о скрытых причинах, просто ищет оптимальные линейные комбинации наблюдаемых переменных.
Цель факторного анализа — найти небольшое число латентных (скрытых) факторов, которые объясняют корреляции между наблюдаемыми переменными. Предполагается, что за измеряемыми характеристиками стоят более фундаментальные причины.
| Критерий | PCA | Факторный анализ |
|---|---|---|
| Математическая модель | Детерминистическая | Стохастическая (с ошибками) |
| Фокус | Максимизация объясненной дисперсии | Объяснение корреляций |
| Предположения | Минимальные | Наличие латентных факторов |
| Уникальная дисперсия | Включается в компоненты | Выделяется отдельно |
| Интерпретация | Искусственные оси | Содержательные факторы |
Когда применять: для предобработки данных в машинном обучении, снижения вычислительной сложности, визуализации многомерных данных, сжатия информации без потери качества.
Когда применять факторный анализ: для психометрических исследований (выявление черт личности), социологических опросов (скрытые установки), экономического анализа (макроэкономические индикаторы), везде, где важно найти содержательную интерпретацию скрытых причин.
На практике выбор между методами определяется исследовательской задачей: нужна ли нам просто эффективная система координат (PCA) или мы ищем объяснение природы изучаемого явления (факторный анализ)?
Альтернативы: когда нужны другие методы
Метод главных компонент — не единственное решение задач снижения размерности. Развитие машинного обучения предложило множество альтернатив, каждая из которых имеет свои преимущества в конкретных ситуациях.
Автоэнкодеры представляют нейросетевой подход к сжатию данных. В отличие от PCA, они могут выявлять нелинейные зависимости и работать с любыми типами данных — от изображений до текстов. Вариационные автоэнкодеры (VAE) дополнительно позволяют генерировать новые образцы, похожие на исходные данные.
t-SNE (t-distributed Stochastic Neighbor Embedding) специализируется на визуализации — создании двумерных карт многомерных данных. Метод превосходно сохраняет локальную структуру, показывая кластеры и группировки, но глобальные расстояния могут искажаться. Стал стандартом для визуализации в биоинформатике и анализе социальных сетей.
UMAP (Uniform Manifold Approximation and Projection) — современная альтернатива t-SNE, которая лучше сохраняет глобальную структуру данных и работает значительно быстрее. Особенно эффективен для больших наборов данных и интерактивной визуализации.
SOM (Self-Organizing Maps) создают топологические карты данных, где похожие объекты располагаются рядом. Метод популярен в маркетинге для сегментации клиентов и в нейронауке для анализа активности мозга.
| Метод | Преимущества | Недостатки | Лучшее применение |
|---|---|---|---|
| PCA | Простота, интерпретируемость | Только линейные связи | Предобработка, быстрая визуализация |
| t-SNE | Отличная визуализация кластеров | Медленный, искажает расстояния | Разведочный анализ |
| Autoencoder | Нелинейности, любые данные | Сложность настройки | Глубокое обучение |
| UMAP | Скорость, сохранение структуры | Новизна метода | Большие данные |
Выбор метода зависит от задачи: для быстрой предобработки берём PCA, для красивой визуализации — t-SNE или UMAP, для работы с изображениями — автоэнкодеры. Понимание сильных и слабых сторон каждого подхода — ключ к успешному анализу данных.
Заключение
Метод главных компонент остаётся одним из фундаментальных инструментов анализа данных, несмотря на появление более сложных альтернатив. Его главные преимущества — математическая элегантность, вычислительная эффективность и предсказуемость результатов.
Основные выводы:
- PCA упрощает структуру данных. Он делает их компактнее и удобнее для анализа.
- Метод работает только при наличии корреляций. Если признаки независимы или нелинейны — эффект минимален.
- Выбор количества компонент — ключ к балансу между точностью и простотой.
- Модификации PCA расширяют его возможности. Это важно для работы с шумом и сложными структурами.
- Визуализация результатов — сильная сторона PCA. Она помогает интерпретировать данные и принимать решения.
Если вы только начинаете осваивать аналитику данных, рекомендуем обратить внимание на подборку курсов по системной аналитике. В курсах есть и теоретическая часть, и практика: от обработки датасетов до визуализации главных компонент.
Рекомендуем посмотреть курсы по системной аналитике
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Аналитик данных
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
105 900 ₽
|
От
8 825 ₽/мес
Беспроцентная. На 1 год.
|
Длительность
6 месяцев
|
Старт
3 февраля
|
Ссылка на курсПодробнее |
|
Системный и бизнес-анализ в разработке ПО. Интенсив
|
Level UP
36 отзывов
|
Цена
75 000 ₽
|
От
18 750 ₽/мес
|
Длительность
1 месяц
|
Старт
23 января
|
Ссылка на курсПодробнее |
|
Системный аналитик PRO
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
79 800 ₽
140 000 ₽
|
От
3 500 ₽/мес
Рассрочка на 2 года.
|
Длительность
10 месяцев
|
Старт
13 февраля
|
Ссылка на курсПодробнее |
|
Системный аналитик с нуля
|
Stepik
33 отзыва
|
Цена
4 500 ₽
|
|
Длительность
1 неделя
|
Старт
в любое время
|
Ссылка на курсПодробнее |
|
Системный аналитик с нуля до PRO
|
Eduson Academy
100 отзывов
|
Цена
Ещё -10% по промокоду
125 900 ₽
257 760 ₽
|
От
10 492 ₽/мес
10 740 ₽/мес
|
Длительность
6 месяцев
|
Старт
в любое время
|
Ссылка на курсПодробнее |

Онбординг персонала: как не отпугнуть новичка в первый день?
Как сделать так, чтобы новый сотрудник не сбежал через неделю? Разбираем, что такое онбординг персонала, какие этапы он включает и как он влияет на адаптацию.

Почему ваши уведомления в iOS бесят — и как это исправить
Уведомления в iOS могут быть полезными, а не назойливыми. В этом гайде — примеры, техники и тонкости, о которых забывают даже опытные разработчики.

Что такое тестирование на отказоустойчивость и зачем оно нужно
Что делать, если база данных откажет, а сервер перегреется? Расскажем, как работает тестирование отказоустойчивости и как оно помогает избежать катастроф даже при серьёзных сбоях.

Что такое модуль числа и зачем он нужен в Excel
Хотите понять, зачем нужен модуль в Excel и как он помогает анализировать данные без лишних формул? В этой статье разберём всё на простых примерах с функцией ABS и покажем, где её применение особенно удобно.