Что такое метод математической индукции и как он работает
В мире аналитики и программирования существует множество инструментов, позволяющих проверить гипотезы и оптимизировать алгоритмы. Один из таких инструментов — метод математической индукции — незаменим, когда речь идет о доказательстве утверждений для всех натуральных чисел. В этом курсе мы разберемся, что представляет собой математическая индукция, как она работает и в каких случаях может стать незаменимым помощником для специалистов в сфере технологий и аналитики.

Этот метод активно применяется в Data Science, бизнес-аналитике и программировании для проверки корректности моделей прогнозирования и алгоритмов. Возможно, вы уже неосознанно использовали его принципы в работе, даже не подозревая об этом.
- Что такое математическая индукция
- Индукция vs дедукция — в чём разница
- Как работает метод математической индукции
- Примеры применения математической индукции
- Где применяется математическая индукция в реальной жизни
- Как научиться использовать индукцию на практике
- Краткое резюме
- Рекомендуем посмотреть курсы по системной аналитике
Что такое математическая индукция
Математическая индукция — это метод доказательства, который позволяет установить истинность некоторого утверждения для всех натуральных чисел. По своей сути, он напоминает принцип падающих костяшек домино: если мы убедимся, что первая костяшка падает, и что падение любой костяшки приводит к падению следующей, то логично заключить, что упадут все костяшки в ряду, сколько бы их ни было.
В более формальном виде, мы доказываем два ключевых момента: (1) утверждение верно для начального числа (обычно 1 или 0) и (2) если утверждение верно для некоторого произвольного числа k, то оно также верно для числа k+1. Эти два условия вместе гарантируют, что утверждение будет верно для всех натуральных чисел, начиная с исходного.
Это мощный математический инструмент, который особенно полезен, когда нам необходимо доказать закономерность для бесконечного множества чисел. Вместо того чтобы проверять каждое число отдельно (что невозможно для бесконечности), мы создаем своеобразную цепную реакцию доказательств, где каждое последующее звено автоматически подтверждается предыдущим.
При этом математическая индукция — не просто теоретический инструмент. Она находит применение в различных сферах: от проверки корректности рекурсивных алгоритмов в программировании до построения прогностических моделей в аналитике. Владение этим методом позволяет специалистам в области технологий эффективно решать широкий спектр задач, требующих доказательства последовательных зависимостей.
Индукция vs дедукция — в чём разница
В процессе аналитического мышления мы часто используем два противоположных подхода: индукцию и дедукцию. Хотя оба метода служат для получения логических выводов, путь рассуждений в них диаметрально противоположен.
Дедукция движется от общего к частному: мы начинаем с известного правила или закона и применяем его к конкретной ситуации. Этот метод широко использовал знаменитый литературный детектив Шерлок Холмс, хотя, вопреки распространенному мнению, его метод чаще основывался именно на индукции.
Индукция же строится от частного к общему: на основе наблюдений за отдельными случаями формулируются общие правила. Математическая индукция представляет собой формализованный вариант такого подхода, где вместо приблизительных выводов мы получаем строгое доказательство.
| Индукция | Дедукция |
|---|---|
| От частного к общему | От общего к частному |
| «Все наблюдаемые вороны черные, значит, все вороны черные» | «Все вороны черные, эта птица — ворона, значит, она черная» |
| Расширяет знания, но результат может быть неточным | Дает достоверные выводы при верных исходных утверждениях |
| Используется для выдвижения гипотез и теорий | Применяется для практического применения законов |
| В математической индукции формализуется через доказательство базы и шага | В математике применяется через аксиомы и теоремы |
Важно понимать, что, в отличие от обычной индукции в логике, математическая индукция является строгим методом доказательства и не допускает вероятностных выводов. Она гарантирует абсолютную достоверность утверждения для всех натуральных чисел, если правильно выполнены все этапы доказательства.
Как работает метод математической индукции
Метод математической индукции представляет собой четко структурированный процесс, который при правильном применении становится мощным инструментом доказательства. Разберем пошагово, как работает этот метод, чтобы вы могли уверенно использовать его для решения своих задач.
Шаг 1. Формулировка утверждения
На этом этапе мы четко определяем, что именно намерены доказать. Утверждение должно быть сформулировано для всех натуральных чисел, начиная с некоторого значения. Например: «Для любого натурального числа n ≥ 1 выполняется равенство 1 + 2 + 3 + … + n = n(n+1)/2».
Формулировка должна быть предельно точной — любая неопределенность может привести к ошибкам в доказательстве. Обратите внимание на область применения утверждения: иногда она начинается с нуля, иногда с единицы или другого натурального числа.
Шаг 2. Базовый шаг (n = 1)
Здесь мы проверяем, верно ли наше утверждение для начального значения (обычно n = 1 или n = 0). Это фундамент всего доказательства — та первая костяшка домино, которая должна упасть.
Для базового шага просто подставляем начальное значение в нашу формулу и проверяем результат. Если для n = 1 утверждение истинно, мы переходим к следующему шагу. Если нет — доказательство невозможно, и утверждение неверно.
Шаг 3. Индукционное предположение
На этом этапе мы делаем ключевое допущение: предполагаем, что наше утверждение верно для некоторого произвольного, но фиксированного натурального числа k. Важно понимать, что мы не доказываем это предположение — мы принимаем его как гипотезу для следующего шага.
Это похоже на ситуацию, когда мы говорим: «Допустим, что костяшка с номером k уже упала». Мы не пытаемся доказать, что она упала — мы лишь используем это предположение, чтобы показать, что упадет и следующая костяшка.
Шаг 4. Индукционный шаг (n → n+1)
Здесь происходит основное доказательство. Мы должны показать, что если утверждение верно для числа k, то оно будет верно и для числа k+1. Это критически важный момент — мы устанавливаем связь между соседними числами.
Технически это выглядит так: мы начинаем с формулы для k+1 и путем алгебраических преобразований пытаемся свести ее к формуле для k, которую мы приняли как верную на шаге 3. Если нам удается доказать, что из истинности утверждения для k следует его истинность для k+1, то с учетом базового шага мы доказали утверждение для всех натуральных чисел в заданном диапазоне.
Именно этот момент обеспечивает «эффект домино» — убедившись, что каждое число «передает эстафету» следующему, мы доказываем всю цепочку целиком.
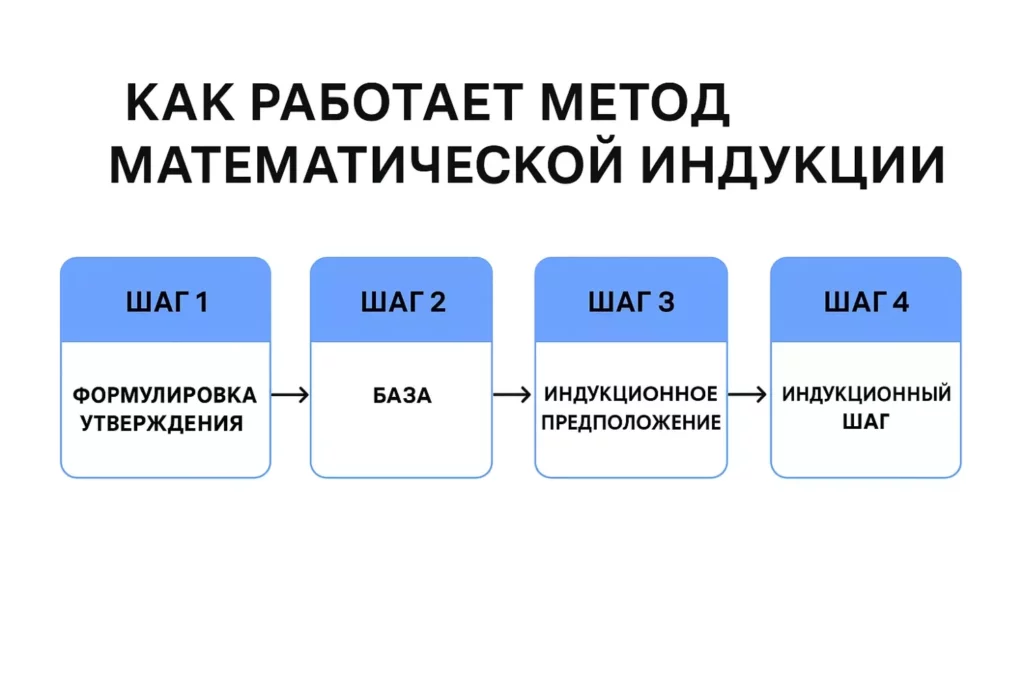
Диаграмма представляет собой схему из четырёх блоков, иллюстрирующих пошаговый процесс математической индукции
Корректное выполнение всех четырех шагов гарантирует математическую строгость доказательства. В отличие от эмпирических методов, где мы могли бы проверить утверждение для нескольких значений и предположить его общую истинность, метод математической индукции дает абсолютную уверенность в результате для всех натуральных чисел.
Примеры применения математической индукции
Пример 1: сумма натуральных чисел
Рассмотрим классический пример, который часто встречается в учебниках и демонстрирует все шаги метода математической индукции. Мы докажем формулу для суммы первых n натуральных чисел.
Утверждение:
Для любого натурального числа n ≥ 1 сумма 1 + 2 + 3 + … + n равна n(n+1)/2.
Шаг 1. Формулировка утверждения
Мы хотим доказать, что для всех натуральных n ≥ 1: 1 + 2 + 3 + … + n = n(n+1)/2
Шаг 2. Базовый шаг (n = 1)
Проверим истинность утверждения для n = 1: Левая часть: 1 Правая часть: 1(1+1)/2 = 1·2/2 = 1
Левая часть равна правой, значит, для n = 1 утверждение верно.
Шаг 3. Индукционное предположение
Предположим, что для некоторого k ≥ 1 утверждение верно, то есть: 1 + 2 + 3 + … + k = k(k+1)/2
Шаг 4. Индукционный шаг (k → k+1)
Нужно доказать, что утверждение верно для k+1, то есть: 1 + 2 + 3 + … + k + (k+1) = (k+1)(k+2)/2
Рассмотрим левую часть этого равенства: 1 + 2 + 3 + … + k + (k+1)
По индукционному предположению: 1 + 2 + 3 + … + k = k(k+1)/2
Значит: 1 + 2 + 3 + … + k + (k+1) = k(k+1)/2 + (k+1)
Преобразуем правую часть: k(k+1)/2 + (k+1) = (k(k+1) + 2(k+1))/2 = (k+1)(k+2)/2
Итак, мы доказали, что: 1 + 2 + 3 + … + k + (k+1) = (k+1)(k+2)/2
Что и требовалось доказать. Таким образом, формула суммы первых n натуральных чисел n(n+1)/2 верна для всех натуральных чисел n ≥ 1.
Пример 2: применение в программировании и аналитике
В мире разработки и анализа данных математическая индукция часто применяется для проверки корректности алгоритмов, особенно рекурсивных. Рассмотрим практический пример с алгоритмом вычисления факториала.
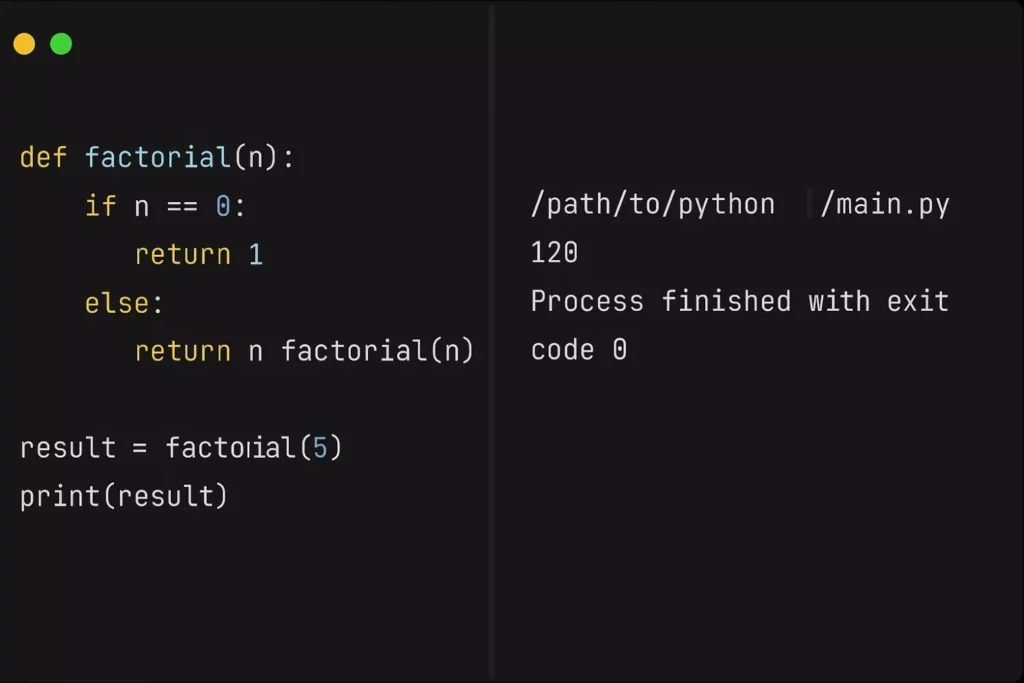
Скриншот демонстрирует окно IDE (интегрированной среды разработки) с открытым кодом на Python. Слева показана реализация рекурсивной функции factorial(n), включающая базовый случай для n = 0 и рекурсивный вызов для остальных значений. Ниже расположен вызов функции с аргументом 5 и вывод результата.
Утверждение:
Рекурсивная функция для вычисления факториала корректно работает для всех натуральных чисел n ≥ 0.
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
Шаг 1. Формулировка утверждения
Мы утверждаем, что функция factorial(n) правильно вычисляет n! для всех n ≥ 0.
Шаг 2. Базовый шаг (n = 0)
При n = 0 функция возвращает 1, что соответствует определению 0! = 1. База индукции верна.
Шаг 3. Индукционное предположение
Предположим, что для некоторого k ≥ 0 функция factorial(k) правильно вычисляет k!.
Шаг 4. Индукционный шаг (k → k+1)
Нам нужно доказать, что factorial(k+1) правильно вычисляет (k+1)!.
По определению функции: factorial(k+1) = (k+1) * factorial(k)
По индукционному предположению factorial(k) = k!
Следовательно: factorial(k+1) = (k+1) * k! = (k+1)!
Что и требовалось доказать. Таким образом, мы убедились, что наша рекурсивная функция корректно вычисляет факториал для всех натуральных чисел n ≥ 0.
В данном примере математическая индукция позволила нам не только убедиться в корректности алгоритма, но и понять механизм его работы. Это особенно ценно при анализе сложных рекурсивных процессов, когда каждый шаг зависит от предыдущих вычислений.
Где применяется математическая индукция в реальной жизни
В то время как математическая индукция может показаться сугубо теоретическим инструментом, её практическое применение гораздо шире, чем можно предположить. Этот метод доказательства находит применение во многих сферах современных технологий и бизнеса.
В сфере информационных технологий математическая индукция служит фундаментальным инструментом для проверки корректности алгоритмов. Разработчики используют её для доказательства того, что созданный ими код будет работать для любого объёма входных данных. Особенно ценно это при работе с рекурсивными функциями и структурами данных, такими как деревья или графы.
В Data Science индукция позволяет математически обосновать модели машинного обучения и предсказательные алгоритмы. Когда аналитик создаёт модель прогнозирования, критически важно удостовериться, что она будет работать корректно для всех возможных временных периодов и объёмов данных. Индукция предоставляет строгий математический фреймворк для подобных проверок.
В финансовом секторе метод математической индукции применяется для моделирования долгосрочных процессов, например, оценки роста инвестиций или прогнозирования доходности. Если формула расчёта доказана с помощью индукции, мы можем быть уверены, что она верна для любого количества периодов.
В бизнес-аналитике индукция служит инструментом для проверки различных гипотез о росте показателей. Например, аналитик может использовать этот метод, чтобы математически обосновать прогноз роста клиентской базы при заданных условиях или убедиться, что планируемый объём производства сможет удовлетворить растущий спрос.
В маркетинге индукция может применяться для моделирования виральности контента или прогнозирования LTV (пожизненной ценности клиента). Если мы можем математически доказать, что каждый новый пользователь приводит в среднем более одного нового пользователя, мы можем с уверенностью говорить о виральном росте.
Даже в таких областях, как логистика и управление цепями поставок, математическая индукция находит применение для оптимизации маршрутов и распределения ресурсов, когда нужно доказать оптимальность решения для произвольного количества узлов или точек.

Горизонтальная иллюстрация демонстрирует ключевые области, где применяется математическая индукция
Все эти примеры демонстрируют, что математическая индукция — не просто теоретический конструкт, а практический инструмент, который помогает специалистам в различных областях принимать обоснованные решения и разрабатывать надёжные алгоритмы и модели.
Как научиться использовать индукцию на практике
Овладение методом математической индукции открывает широкие возможности для профессионального роста специалистов в области технологий и аналитики. К счастью, существует множество ресурсов, которые помогут вам развить эти навыки.
Для начинающих мы рекомендуем обратить внимание на онлайн-курсы, которые охватывают основы дискретной математики. Практически все качественные программы по математике для инженеров и аналитиков включают разделы, посвященные методу математической индукции:
- Курс «Математика в анализе данных», который за шесть месяцев последовательно знакомит с линейной алгеброй, математическим анализом и другими разделами, необходимыми для аналитика
- Специализация «Дискретная математика для информатиков» на популярных образовательных платформах
- Интерактивные курсы на Khan Academy в разделе «Дискретная математика»
Если вы предпочитаете учиться по книгам, стоит обратить внимание на следующие издания:
- «Дискретная математика для программистов» Р. Грэхема, Д. Кнута и О. Паташника
- «Конкретная математика» Д. Кнута — классический учебник, где индукция рассматривается в контексте решения реальных алгоритмических задач
- «Дискретная математика и её приложения» К. Россена — содержит множество примеров применения индукции в компьютерных науках
Для тех, кто предпочитает практический подход, существуют сборники задач с подробными решениями:
- Project Euler — интернет-проект, содержащий множество математических и программистских задач
- Leetcode и HackerRank — разделы с алгоритмическими задачами, многие из которых можно решить или проанализировать с помощью индукции
Регулярная практика — ключ к успеху. Начните с простых примеров, подобных тем, что мы рассмотрели в статье, и постепенно переходите к более сложным задачам. Постоянное применение метода математической индукции в реальных проектах поможет довести навык до автоматизма.
Краткое резюме
Подводя итоги, метод математической индукции представляет собой мощный инструмент, который открывает перед аналитиками, программистами и специалистами в области Data Science широкие возможности для доказательства утверждений и проверки алгоритмов. Мы рассмотрели основные принципы этого метода, включая формулировку утверждения, базовый шаг, индукционное предположение и индукционный переход.
В отличие от эмпирических методов, которые опираются на конечное число наблюдений, математическая индукция даёт нам строгое доказательство для бесконечного множества случаев. Это особенно ценно в мире технологий, где масштабы данных и количество итераций могут быть огромными.
Применение метода математической индукции выходит далеко за рамки теоретической математики и находит своё место в разработке алгоритмов, аналитике данных, финансовом моделировании, маркетинге и многих других сферах.
Чтобы начать успешно применять этот метод, не требуется глубокого погружения в математические теории — достаточно понять основной принцип и отработать его на практических примерах. Постепенно переходя от простых задач к более сложным, вы сможете сделать метод математической индукции неотъемлемой частью своего профессионального инструментария.
Математическая индукция — важный инструмент в арсенале системного аналитика. Освоение этого метода наряду с другими математическими концепциями значительно повышает эффективность работы с алгоритмами и моделями данных. Если вы хотите комплексно развиваться в аналитике и получить все необходимые навыки для профессии, рекомендуем изучить лучшие курсы системного аналитика, где представлены программы от ведущих образовательных платформ. Эти курсы включают в себя не только математические основы, но и практические инструменты для работы с данными, проектирования систем и бизнес-анализа.
Рекомендуем посмотреть курсы по системной аналитике
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Аналитик данных
|
Eduson Academy
110 отзывов
|
Цена
109 900 ₽
|
От
9 158 ₽/мес
Беспроцентная. На 1 год.
|
Длительность
6 месяцев
|
Старт
3 марта
|
Подробнее |
|
Системный аналитик PRO
|
Нетология
46 отзывов
|
Цена
79 800 ₽
140 000 ₽
с промокодом kursy-online
|
От
3 500 ₽/мес
Рассрочка на 2 года.
|
Длительность
10 месяцев
|
Старт
13 марта
|
Подробнее |
|
Системный аналитик с нуля
|
Stepik
33 отзыва
|
Цена
4 500 ₽
|
|
Длительность
1 неделя
|
Старт
в любое время
|
Подробнее |
|
Системный аналитик с нуля до PRO
|
Eduson Academy
110 отзывов
|
Цена
129 900 ₽
257 760 ₽
Ещё -10% по промокоду
|
От
10 825 ₽/мес
10 740 ₽/мес
|
Длительность
6 месяцев
|
Старт
в любое время
|
Подробнее |

Как ИИ делает роботов умнее: от беспилотников до медицины
Сегодня роботы не просто выполняют команды — они анализируют окружающий мир и обучаются. Узнайте, как искусственный интеллект позволяет им работать эффективнее и что ждёт нас дальше.

Webflow: конструктор сайтов или полноценный инструмент веб-разработки?
Webflow — это больше, чем просто конструктор. Он объединяет дизайн, код и хостинг в одной платформе, позволяя создавать сложные проекты без программирования.

SQL-индексы: что это и как правильно применять в базе данных
Зачем нужны индексы в SQL и почему они могут как ускорить, так и замедлить работу базы? В статье — разбор всех видов индексов, практические советы и примеры кода.

Что такое Data Literacy — зачем нужна грамотность в работе с данными
Хотите понять, почему умение читать и анализировать данные становится базовым навыком XXI века? В этой статье мы простыми словами объясним, что такое data literacy, зачем она нужна и как развить её с нуля.