Методы сортировки: полный разбор и сравнение алгоритмов от пузырьковой до быстрой
Сортировка данных — одна из фундаментальных операций в программировании, которая лежит в основе бесчисленного множества приложений. От поисковых систем до баз данных, от рекомендательных алгоритмов до финансовых платформ — везде требуется упорядочивание информации. Однако за кажущейся простотой этой задачи скрывается целый мир различных подходов, каждый из которых обладает своими особенностями, преимуществами и ограничениями.

Она представляет собой процесс упорядочивания элементов массива или списка согласно определенному критерию — чаще всего по возрастанию или убыванию значений. На первый взгляд эта операция может показаться тривиальной, однако её значение для современных вычислительных систем трудно переоценить. По сути, сортировка является базовым строительным блоком для множества более сложных алгоритмов и структур данных.
Иллюстрация показывает базовую суть сортировки — переход от хаотичных данных к упорядоченному массиву. Помогает быстро понять смысл операции без погружения в алгоритмы.
Рассмотрим практические сценарии, где она играет ключевую роль:
- Поисковые системы и базы данных — упорядоченные данные позволяют применять бинарный поиск, что снижает время поиска с O(n) до O(log n)
- E-commerce платформы — сортировка товаров по цене, рейтингу или популярности напрямую влияет на пользовательский опыт.
- Финансовые приложения — упорядочивание транзакций по дате, сумме или статусу необходимо для анализа и отчетности.
- Социальные сети — ранжирование постов в ленте новостей основано на сложных алгоритмах.
- Аналитика и визуализация данных — построение графиков и диаграмм требует предварительной сортировки массивов значений.
Понимание различных методов необходимо разработчикам по нескольким причинам. Во-первых, выбор неподходящего алгоритма может критически снизить производительность приложения — особенно при работе с большими объемами данных. Во-вторых, знание внутренних механизмов помогает оптимизировать существующий код и избегать типичных ошибок. Наконец, многие способы демонстрируют фундаментальные принципы программирования — рекурсию, разделение задач, работу с памятью — которые применимы далеко за пределами самой сортировки.
- Основные критерии сравнения
- Примитивные (базовые) алгоритмы сортировки
- Сортировка выбором (Selection Sort)
- Продвинутые алгоритмы
- Быстрая сортировка (Quick Sort)
- Пирамидальная сортировка (Heap Sort)
- Примеры кода реализаций алгоритмов
- Сравнение по ключевым параметрам
- Углублённые аспекты работы
- Гибридные и практические алгоритмы, используемые в реальных языках
- Заключение
- Рекомендуем посмотреть курсы по Python
Основные критерии сравнения
Прежде всего необходимо определить критерии, по которым мы будем их оценивать. Эффективность сортировки не сводится к одному параметру — различные аспекты могут иметь разный приоритет в зависимости от конкретной задачи.
Временная сложность. Это основной показатель производительности, который измеряет количество операций в зависимости от размера входных данных. Мы различаем три сценария:
- Лучший случай — минимальное время выполнения при наиболее благоприятных входных данных (например, уже отсортированный массив).
- Средний случай — ожидаемое время для типичных, случайных данных.
- Худший случай — максимальное время при наихудшем расположении элементов.
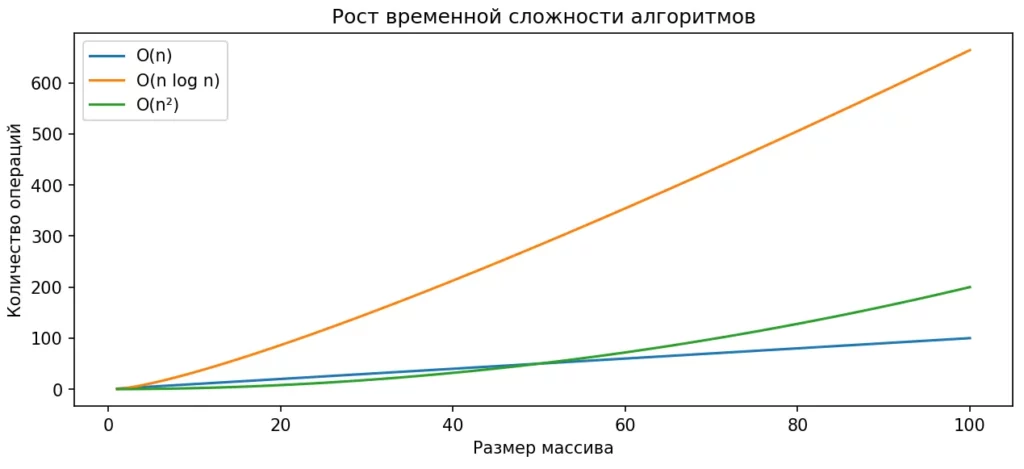
График показывает, как растёт количество операций при увеличении размера массива. Видно, почему алгоритмы с O(n²) быстро становятся непригодными, а O(n log n) остаются эффективными даже на больших данных.
Пространственная сложность. Определяет объем дополнительной памяти, необходимой для работы алгоритма. Здесь выделяют:
- In-place — требуется O(1) дополнительной памяти, сортируют массив «на месте».
- Out-of-place — создаются дополнительные структуры данных, что увеличивает потребление памяти.
Стабильность. Стабильный алгоритм сохраняет относительный порядок элементов с одинаковыми ключами. Если два элемента равны, они останутся в той же последовательности, что и до сортировки. Это критично при многоуровневой сортировке — например, когда нужно сначала отсортировать по дате, затем по приоритету.
Адаптивность. Адаптивный эффективнее работает на частично отсортированных данных, приближая временную сложность к оптимальной O(n). Неадаптивные алгоритмы выполняют одинаковое количество операций независимо от начального порядка элементов.
Метод сравнения. Большинство алгоритмов используют операции сравнения элементов (<, >, =). Однако существуют и несравнительные методы, такие как поразрядная сортировка, которые могут достигать линейной сложности O(n) при определенных условиях.
Примитивные (базовые) алгоритмы сортировки
Базовые служат фундаментом для понимания более сложных методов. Несмотря на их относительную неэффективность на больших массивах, они обладают простотой реализации и могут быть оптимальными для специфических сценариев — например, при работе с малыми объемами данных или когда важна минимальная сложность кода.

Иллюстрация показывает, как человек работает с неупорядоченными данными и приводит их в логичный порядок с помощью сортировки. Такой переход от хаоса к структуре наглядно отражает суть алгоритмов сортировки и их практическую пользу.
Пузырьковая (Bubble Sort)
Получила свое название из-за того, что элементы постепенно «всплывают» к своим позициям, подобно пузырькам воздуха в воде. Алгоритм работает следующим образом: на каждой итерации происходит последовательное попарное сравнение соседних элементов, и если порядок нарушен — они меняются местами. В результате после первого прохода наибольший элемент гарантированно оказывается в конце массива.
Ключевые особенности:
- Алгоритм повторяет проходы по массиву, с каждым разом сокращая диапазон проверки на один элемент (поскольку последние элементы уже отсортированы).
- Возможна оптимизация с флагом: если за весь проход не произошло ни одного обмена — массив уже отсортирован, и алгоритм завершается досрочно.
Сложность: O(n²) в среднем и худшем случае, O(n) в лучшем случае при использовании оптимизации. Пространственная сложность — O(1), алгоритм работает in-place.
Стабильность: стабильный алгоритм, поскольку равные элементы не меняются местами.
Когда использовать: пузырьковая сортировка оправдана только для учебных целей или при работе с очень малыми массивами (до 10-15 элементов), где простота реализации важнее производительности. В производственном коде практически не применяется из-за низкой эффективности.
Сортировка выбором (Selection Sort)
Основана на интуитивно понятной идее: на каждом шаге алгоритм находит минимальный элемент в неотсортированной части массива и перемещает его в начало этой части. Процесс повторяется до тех пор, пока весь массив не будет упорядочен. По сути, мы постепенно формируем отсортированную часть слева, расширяя её на один элемент с каждой итерацией.
Ключевые особенности:
- Алгоритм выполняет минимальное количество обменов элементов — максимум n-1 перестановок для массива из n элементов. Это может быть преимуществом, если операция обмена ресурсоёмкая.
- Неадаптивность: алгоритм всегда выполняет одинаковое количество сравнений независимо от начального порядка данных.
- Нестабильность: при перемещении минимального элемента в начало может нарушаться относительный порядок равных элементов.
Сложность: O(n²) во всех случаях — лучшем, среднем и худшем. Это делает сортировку выбором предсказуемой, но неэффективной. Пространственная сложность составляет O(1).
Сортировка выбором редко применяется в практических задачах из-за квадратичной временной сложности и отсутствия адаптивности. Однако она может быть полезна в системах с ограниченной памятью, где критично минимальное количество операций записи, или в качестве вспомогательного инструмента для обучения базовым концепциям алгоритмов.
Сортировка вставками (Insertion Sort)
Работает по принципу, знакомому каждому, кто когда-либо раскладывал карты в руке во время игры. Алгоритм поддерживает отсортированную часть массива слева и последовательно берет элементы из неотсортированной части, вставляя каждый на подходящую позицию в отсортированный фрагмент. Для этого элемент сравнивается с предыдущими и «сдвигается» влево до тех пор, пока не найдет свое место.
Ключевые особенности:
- Адаптивность — это главное преимущество. На частично отсортированных данных сложность приближается к O(n), поскольку требуется минимальное количество сдвигов.
- Стабильность: алгоритм сохраняет относительный порядок равных элементов, так как вставка происходит после элементов с таким же значением.
- Эффективность на малых массивах: благодаря низким константам и простоте реализации сортировка вставками часто быстрее более сложных алгоритмов на массивах до 10-20 элементов.
Сложность: O(n²) в среднем и худшем случае (когда массив отсортирован в обратном порядке), O(n) в лучшем случае (массив уже отсортирован). Пространственная сложность — O(1).
Плюсы и минусы: сортировка вставками оптимальна для небольших массивов, почти отсортированных данных и онлайн-сортировки (когда элементы поступают последовательно). Именно поэтому она используется в гибридных алгоритмах вроде TimSort в качестве завершающего этапа для мелких подмассивов. Однако на больших случайных данных её производительность значительно уступает продвинутым методам.
Продвинутые алгоритмы
Продвинутые представляют качественный скачок в эффективности по сравнению с базовыми методами. Они используют более сложные стратегии — рекурсивное разделение задачи, специальные структуры данных, оптимизированные схемы работы с памятью. Временная сложность их составляет O(n log n) в среднем или лучшем случае, что делает их применимыми для работы с массивами из тысяч и миллионов элементов.
Быстрая сортировка (Quick Sort)
Она заслуженно считается одним из наиболее эффективных алгоритмов общего назначения и широко применяется в стандартных библиотеках многих языков программирования. Он основан на стратегии «разделяй и властвуй» (divide and conquer): массив рекурсивно разбивается на части относительно выбранного опорного элемента (pivot).
Принцип работы: На каждом шаге рекурсии выбирается pivot, после чего массив разделяется на три части: элементы меньше pivot, равные pivot и больше pivot. Затем алгоритм рекурсивно применяется к левой и правой частям. Когда подмассив содержит один элемент или пуст — рекурсия завершается.
Выбор опорного элемента: От выбора pivot критически зависит производительность. Простейший вариант — брать первый, последний или средний элемент — может привести к деградации до O(n²) на отсортированных или почти отсортированных данных. Более надежная стратегия — рандомизация выбора pivot или метод «медианы трёх» (выбор медианы среди первого, среднего и последнего элементов).
Сложность: средняя временная сложность составляет O(n log n), худшая — O(n²) при неудачном выборе pivot. Пространственная сложность — O(log n) для рекурсивного стека вызовов. Алгоритм работает in-place, не требуя дополнительных массивов.
Стабильность: нестабильный алгоритм, поскольку в процессе разделения элементы могут перемещаться на значительные расстояния.
Когда использовать: быстрая сортировка оптимальна для больших массивов случайных данных, где средняя производительность важнее гарантий худшего случая. Она особенно эффективна благодаря хорошей локальности обращений к памяти, что положительно влияет на работу кеша процессора.
Сортировка слиянием (Merge Sort)
Это классический пример применения парадигмы «разделяй и властвуй», который гарантирует предсказуемую производительность независимо от характера входных данных. Алгоритм рекурсивно делит массив пополам до тех пор, пока не получатся подмассивы из одного элемента, а затем последовательно объединяет (сливает) их обратно, сохраняя упорядоченность.
Принцип работы:
На этапе разделения массив рекурсивно делится на две равные части до достижения базового случая (массив из одного элемента считается отсортированным). Затем начинается обратный процесс — слияние: два отсортированных подмассива объединяются в один отсортированный массив путём последовательного сравнения элементов с начала каждого подмассива и выбора меньшего.
Ключевые особенности:
- Стабильность: при слиянии равные элементы берутся сначала из левого подмассива, что сохраняет их относительный порядок.
- Гарантированная сложность O(n log n) во всех случаях — лучшем, среднем и худшем. Это делает алгоритм предсказуемым и надежным для критичных систем.
- Хорошо подходит для параллелизации: независимые подмассивы могут сортироваться одновременно на разных процессорных ядрах.
Сложность: временная сложность O(n log n) во всех случаях. Пространственная сложность — O(n), поскольку требуется дополнительный массив для хранения результата слияния. Это основной недостаток.
Примеры применимости: сортировка слиянием оптимальна, когда критична стабильность и гарантированная производительность — например, при сортировке связных списков (где она может работать in-place), в системах реального времени или при обработке внешних данных (external sorting), когда массив не помещается в оперативную память. Многие языки программирования используют вариации merge sort для стабильной сортировки объектов.
Пирамидальная сортировка (Heap Sort)
Представляет собой алгоритм, основанный на структуре данных «двоичная куча» (binary heap). Куча — это специальное двоичное дерево, в котором выполняется свойство упорядоченности: в max-heap значение каждого родительского узла больше или равно значениям его потомков, а в min-heap — меньше или равно. Это свойство позволяет эффективно извлекать максимальный (или минимальный) элемент.
Принцип работы:
Алгоритм состоит из двух основных фаз. Сначала из исходного массива строится max-heap — процесс, называемый «heapify». Затем начинается этап сортировки: корень кучи (максимальный элемент) меняется местами с последним элементом массива и помещается в конец отсортированной части. Размер кучи уменьшается на единицу, после чего куча восстанавливается. Процесс повторяется до тех пор, пока размер кучи не станет равным единице.
Ключевые особенности:
- Нестабильность: в процессе построения и перестройки кучи элементы перемещаются на значительные расстояния, что нарушает относительный порядок равных элементов.
- Всегда O(n log n): независимо от входных данных, алгоритм выполняет одинаковое количество операций, что обеспечивает предсказуемость.
- In-place сортировка с O(1) дополнительной памяти — значительное преимущество перед merge sort.
Сложность: временная сложность O(n log n) во всех случаях. Построение кучи требует O(n) времени, а каждое из n извлечений корня — O(log n). Пространственная сложность составляет O(1).
Когда использовать: пирамидальная сортировка имеет смысл в системах с жёсткими ограничениями по памяти, где недопустимо использование дополнительных структур данных, характерных для merge sort. Также она полезна, когда требуется гарантированная производительность O(n log n) без риска деградации до O(n²), как у quick sort. Однако на практике heap sort часто уступает quick sort из-за худшей локальности обращений к памяти и больших констант.
Примеры кода реализаций алгоритмов
Теоретическое понимание необходимо дополнить практическими примерами их реализации. Мы рассмотрим код на Python — языке, чья читаемость позволяет сосредоточиться на логике, а не на синтаксических деталях. Каждая реализация снабжена комментариями, поясняющими ключевые моменты.
Примеры реализации простых алгоритмов
Bubble Sort (Пузырьковая)
def bubble_sort(arr): n = len(arr) for i in range(n): swapped = False # Флаг для оптимизации # Последние i элементов уже на своих местах for j in range(0, n - i - 1): if arr[j] > arr[j + 1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] swapped = True # Если обменов не было -- массив отсортирован if not swapped: break return arr
Insertion Sort (Сортировка вставками)
def insertion_sort(arr): for i in range(1, len(arr)): key = arr[i] # Элемент для вставки j = i - 1 # Сдвигаем элементы вправо, пока не найдем позицию while j >= 0 and arr[j] > key: arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key return arr
Selection Sort (Сортировка выбором)
def selection_sort(arr): n = len(arr) for i in range(n): # Находим индекс минимального элемента min_idx = i for j in range(i + 1, n): if arr[j] < arr[min_idx]: min_idx = j # Меняем местами найденный минимум с первым элементом arr[i], arr[min_idx] = arr[min_idx], arr[i] return arr
Примеры реализации продвинутых алгоритмов
Quick Sort (Быстрая)
def quick_sort(arr): if len(arr) <= 1: return arr # Выбираем pivot (можно использовать random для лучшей производительности) pivot = arr[len(arr) // 2] # Разделяем массив на три части left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] # Рекурсивно сортируем левую и правую части return quick_sort(left) + middle + quick_sort(right)
Merge Sort (Сортировка слиянием)
def merge_sort(arr): if len(arr) <= 1: return arr # Делим массив пополам mid = len(arr) // 2 left = merge_sort(arr[:mid]) right = merge_sort(arr[mid:]) # Сливаем отсортированные половины return merge(left, right) def merge(left, right): result = [] i = j = 0 # Сравниваем элементы из обеих частей while i < len(left) and j < len(right): if left[i] <= right[j]: # <= для стабильности result.append(left[i]) i += 1 else: result.append(right[j]) j += 1 # Добавляем оставшиеся элементы result.extend(left[i:]) result.extend(right[j:]) return result
Heap Sort (Пирамидальная)
def heap_sort(arr): n = len(arr) # Строим max-heap for i in range(n // 2 - 1, -1, -1): heapify(arr, n, i) # Извлекаем элементы из кучи for i in range(n - 1, 0, -1): arr[0], arr[i] = arr[i], arr[0] # Корень в конец heapify(arr, i, 0) # Восстанавливаем кучу return arr def heapify(arr, n, i): largest = i left = 2 * i + 1 right = 2 * i + 2 # Находим наибольший элемент среди родителя и потомков if left < n and arr[left] > arr[largest]: largest = left if right < n and arr[right] > arr[largest]: largest = right # Если наибольший элемент не корень -- меняем и продолжаем if largest != i: arr[i], arr[largest] = arr[largest], arr[i] heapify(arr, n, largest)
Сравнение по ключевым параметрам
Выбор оптимального алгоритма сортировки требует комплексной оценки его характеристик в различных условиях. Мы систематизировали ключевые параметры всех рассмотренных вариантов, чтобы упростить процесс принятия решения.
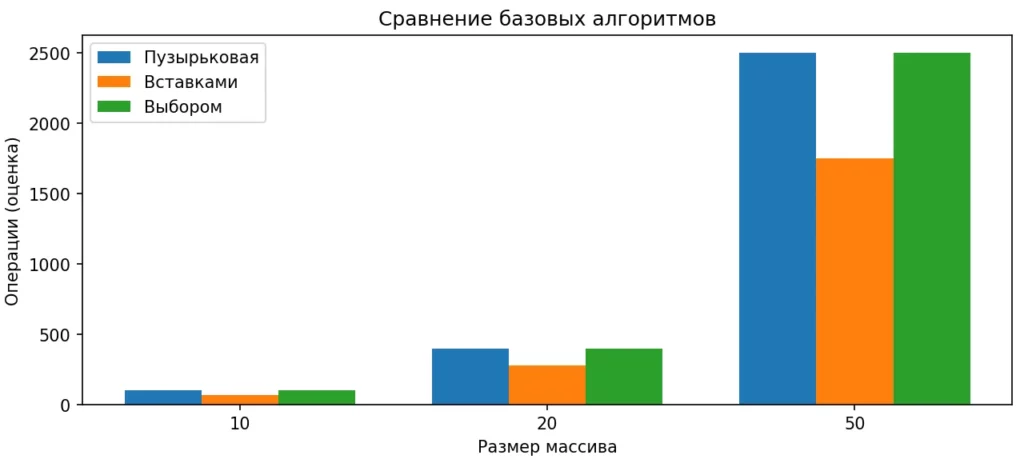
Диаграмма иллюстрирует оценочное количество операций для пузырьковой сортировки, сортировки вставками и выбором. Наглядно видно, почему эти методы плохо масштабируются при росте массива.
Таблица сравнения сложности, памяти и стабильности
| Алгоритм | Лучший случай | Средний случай | Худший случай | Память | Стабильность |
|---|---|---|---|---|---|
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) | ✓ |
| Selection Sort | O(n²) | O(n²) | O(n²) | O(1) | ✗ |
| Insertion Sort | O(n) | O(n²) | O(n²) | O(1) | ✓ |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) | ✗ |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) | ✓ |
| Heap Sort | O(n log n) | O(n log n) | O(n log n) | O(1) | ✗ |
Как видно из таблицы, не существует универсального алгоритма, который превосходил бы остальные по всем параметрам одновременно. Merge Sort гарантирует O(n log n) и стабильность, но требует дополнительной памяти. Quick Sort в среднем работает быстрее всех, но может деградировать до O(n²). Heap Sort сочетает гарантированную производительность с минимальным использованием памяти, но нестабилен и на практике часто медленнее Quick Sort из-за худшей работы с кешем процессора.
Как выбрать алгоритм под конкретную задачу
Выбор алгоритма сортировки должен основываться на анализе конкретных требований и ограничений вашей задачи. Рассмотрим типичные сценарии и оптимальные решения для каждого из них.
- Малые массивы (до 50 элементов).Для небольших объемов данных накладные расходы на рекурсию и сложную логику продвинутых алгоритмов могут перевесить их теоретическое преимущество. Insertion Sort показывает отличную производительность благодаря низким константам и простоте реализации. Именно поэтому гибридные алгоритмы переключаются на сортировку вставками при достижении небольших подмассивов.
- Большие массивы случайных данных. Quick Sort остается лидером для этого сценария. При правильном выборе pivot (рандомизация или медиана трёх) алгоритм демонстрирует превосходную производительность благодаря эффективной работе с кешем процессора и минимальным накладным расходам. Современные реализации в стандартных библиотеках обычно основаны именно на быстрой сортировке.
- Почти отсортированные данные. Здесь безусловным победителем становится Insertion Sort с его адаптивностью и сложностью O(n) в лучшем случае. Если данные поступают последовательно и уже частично упорядочены (например, логи с временными метками), сортировка вставками может оказаться в десятки раз быстрее любого другого метода.
- Жёсткие ограничения по памяти. Когда дополнительная память критична, выбор ограничивается in-place алгоритмами. Heap Sort обеспечивает гарантированную O(n log n) производительность с O(1) дополнительной памяти, что делает его оптимальным для встроенных систем и работы с большими массивами в условиях ограниченных ресурсов.
- Требуется стабильность. Если важно сохранить относительный порядок равных элементов — например, при многоуровневой сортировке объектов — необходимо выбирать между Merge Sort, Insertion Sort или Bubble Sort. Для больших массивов Merge Sort остается единственным практичным вариантом, несмотря на затраты памяти.
- Гарантированная производительность. В системах реального времени или критичных приложениях, где недопустимы непредсказуемые задержки, следует избегать Quick Sort из-за возможной деградации до O(n²). Merge Sort или Heap Sort гарантируют O(n log n) независимо от входных данных.
- Частые повторные сортировки. Если данные требуют многократной сортировки с небольшими изменениями между итерациями, адаптивные алгоритмы вроде Insertion Sort могут значительно сократить общее время обработки.
Углублённые аспекты работы
За пределами теоретической сложности существует ряд практических факторов, которые существенно влияют на реальную производительность алгоритмов сортировки. Понимание этих аспектов позволяет делать более обоснованный выбор и избегать неожиданных проблем с производительностью.
- Адаптивность и её практическое значение. Адаптивные алгоритмы способны использовать существующую упорядоченность в данных для ускорения работы. Insertion Sort — яркий пример: на массиве, где только несколько элементов находятся не на своих местах, он работает почти за линейное время. В реальных приложениях данные редко бывают полностью случайными — логи событий, временные ряды, результаты предыдущих обработок часто содержат частичную упорядоченность, которую адаптивные алгоритмы эффективно используют.
- Влияние архитектуры процессора и кеша. Современные процессоры работают намного быстрее с данными, находящимися в кеше. Алгоритмы с хорошей локальностью обращений к памяти (когда обрабатываются соседние элементы) получают значительное преимущество. Quick Sort превосходит Heap Sort в практических тестах именно благодаря лучшей cache-friendly природе, несмотря на теоретически одинаковую сложность O(n log n). Heap Sort часто обращается к элементам, находящимся далеко друг от друга в памяти, что приводит к частым промахам кеша.
- Особенности поведения в реальных условиях. Константы в нотации Big O, которые мы обычно игнорируем при теоретическом анализе, на практике имеют огромное значение. Merge Sort теоретически выполняет меньше сравнений, чем Quick Sort, но операции копирования массивов при слиянии добавляют накладные расходы. Quick Sort, несмотря на большее количество сравнений, работает преимущественно со свопами, что быстрее при работе с примитивными типами данных.
- Влияние типа данных. Для простых типов (целые числа, числа с плавающей точкой) операции сравнения и обмена выполняются очень быстро. Однако при сортировке сложных объектов или строк операция сравнения может стать узким местом. Selection Sort с его минимальным количеством перестановок может оказаться предпочтительнее, если объекты велики, а их копирование затратно.
- Стабильность как практическое требование. В системах баз данных и при обработке структурированных данных стабильность часто является не просто желательной, а обязательной характеристикой. Представьте сортировку списка сотрудников: сначала по отделам, затем по зарплате внутри каждого отдела. Нестабильный алгоритм может разрушить первичную группировку, делая результат непредсказуемым.
Гибридные и практические алгоритмы, используемые в реальных языках
Теоретические алгоритмы редко используются в чистом виде в производственных системах. Современные языки программирования применяют гибридные подходы, комбинирующие сильные стороны различных методов для достижения оптимальной производительности в широком спектре сценариев.
- TimSort — гибрид для Python и Java. TimSort, разработанный Тимом Петерсом в 2002 году, является стандартным алгоритмом сортировки в Python и Java. Этот гибридный метод объединяет Merge Sort и Insertion Sort, используя их преимущества в зависимости от характера данных. TimSort анализирует входной массив на наличие естественных упорядоченных последовательностей (runs) и использует их для ускорения процесса слияния. Для коротких runs применяется Insertion Sort, поскольку на малых объемах он работает эффективнее рекурсивных методов. Ключевая особенность TimSort — адаптивность: на реальных данных, которые часто содержат частичную упорядоченность, алгоритм демонстрирует производительность значительно лучше теоретического O(n log n). При этом сохраняется стабильность и гарантированная сложность O(n log n) в худшем случае.
- Introsort — улучшенная Quick Sort. Introsort (Introspective Sort), используемый в стандартной библиотеке C++, начинает с Quick Sort, но отслеживает глубину рекурсии. Если глубина превышает определенный порог (обычно 2 * log n), что сигнализирует о возможной деградации производительности, алгоритм переключается на Heap Sort для гарантированного завершения за O(n log n). На финальном этапе для небольших подмассивов применяется Insertion Sort.
- Практические примеры применения гибридов.Гибридные алгоритмы оптимальны практически везде, где требуется универсальное решение: сортировка коллекций в веб-приложениях, обработка данных в аналитических системах, упорядочивание результатов запросов в базах данных. Их адаптивность делает производительность предсказуемой и высокой независимо от характера входных данных, что критично для библиотек общего назначения.
Заключение
Мы рассмотрели широкий спектр алгоритмов сортировки — от простейших до продвинутых гибридных решений. Теперь подведем итоги и сформулируем практические рекомендации для выбора оптимального метода в различных ситуациях:
- Алгоритмы сортировки лежат в основе работы большинства программных систем. Понимание их принципов позволяет писать более эффективный и предсказуемый код.
- У каждого алгоритма есть сильные и слабые стороны. Выбор метода зависит от объёма данных, требований к памяти, стабильности и гарантированной сложности.
- Простые алгоритмы полезны для обучения и малых массивов. Они помогают понять базовые принципы работы с данными.
- Продвинутые методы обеспечивают высокую производительность на больших объёмах информации. Именно они применяются в стандартных библиотеках языков программирования.
- Гибридные алгоритмы объединяют лучшие свойства нескольких подходов. Это делает их универсальными для реальных задач разработки.
Если вы только начинаете осваивать профессию программиста и хотите глубже разобраться в алгоритмах сортировки, рекомендуем обратить внимание на подборку курсов по Python-разработке. В них сочетаются теоретическая база и практические задания, которые помогают закрепить понимание на реальных примерах.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
16 января
|
Ссылка на курсПодробнее |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 января
|
Ссылка на курсПодробнее |
|
Fullstack-разработчик на Python
|
Нетология
45 отзывов
|
Цена
с промокодом kursy-online
146 500 ₽
308 367 ₽
|
От
4 282 ₽/мес
|
Длительность
18 месяцев
|
Старт
15 января
|
Ссылка на курсПодробнее |
|
Python-разработчик
|
Академия Синергия
34 отзыва
|
Цена
с промокодом KURSHUB
91 560 ₽
228 900 ₽
|
От
3 179 ₽/мес
4 552 ₽/мес
|
Длительность
6 месяцев
|
Старт
20 января
|
Ссылка на курсПодробнее |
|
Профессия Python-разработчик
|
Skillbox
214 отзывов
|
Цена
Ещё -20% по промокоду
74 507 ₽
149 015 ₽
|
От
6 209 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
18 января
|
Ссылка на курсПодробнее |

Управленческий учет: инструмент, который меняет бизнес
Хотите эффективно управлять финансами и минимизировать риски? Управленческий учет дает четкую картину бизнеса и помогает принимать стратегические решения.

Почему программисты в кино — не просто герои фантастики
Какие фильмы про программистов действительно раскрывают суть профессии? В этом материале — не только о «Матрице» и «Мистере Роботе», но и о скрытых жемчужинах IT-кино.

Принципы работы протокола EIGRP
Хотите разобраться, что такое протокол eigrp и чем он отличается от других решений? В статье вы найдете разбор механизмов работы, советы по настройке и ответы на типовые вопросы.

Балансировка нагрузки: что это, какие методы существуют и как работают алгоритмы распределения трафика
Балансировка нагрузки серверов — это не только про Round Robin и прокси. Какие алгоритмы действительно работают под высокой нагрузкой, как они влияют на задержки и что учитывать при выборе подхода?