Очередь с приоритетом (Priority Queue): что это такое, как работает и где применяется

Очередь с приоритетом — это особая структура данных, которая расширяет концепцию обычной очереди, добавляя к каждому элементу дополнительную характеристику: приоритет. В отличие от классической очереди, где действует принцип FIFO (First In, First Out — «первым пришёл, первым вышел»), в этой очереди элементы обслуживаются не в порядке добавления, а в соответствии с их важностью.
- Как она работает
- Типы очередей с приоритетом: min-priority и max-priority
- Основные операции Priority Queue
- Реализации очереди с приоритетом: от простых до эффективных
- Как работает бинарная куча в Priority Queue
- Примеры кода реализации Priority Queue
- Где применяется Priority Queue — практические сценарии
- Преимущества и ограничения очередей с приоритетом
- Заключение
- Рекомендуем посмотреть курсы по Python
Как она работает
Давайте рассмотрим базовую логику работы. Представим себе отделение неотложной помощи в больнице: пациенты не обслуживаются строго по очереди прихода — врачи в первую очередь принимают тех, чьё состояние наиболее критично. Аналогично работает и Priority Queue: объект с наивысшим приоритетом всегда извлекается первым, независимо от того, когда он был добавлен в структуру.
Механизм приоритетов решает важную задачу: он позволяет системе эффективно управлять ресурсами там, где одни операции объективно важнее других. Мы можем наблюдать применение этого принципа в планировщиках операционных систем, где задачи с высокой важностью получают процессорное время раньше фоновых, или в сетевых протоколах, где критически важные пакеты данных обрабатываются в первую очередь.
Принцип обслуживания элементов в Priority Queue кардинально отличается от классической очереди, и понимание этого различия критически важно для эффективного использования структуры. В обычной очереди мы имеем дело с линейным порядком: объекты извлекаются строго в той последовательности, в которой были добавлены. Priority Queue разрывает эту линейность, вводя понятие важности каждой записи.
При каждой операции извлечения структура анализирует все содержащиеся в ней данные и выбирает тот объект, чей приоритет является наивысшим на данный момент. Это не означает, что элемент, добавленный позже, не может быть обработан раньше — если его важность выше, он «обгонит» все записи с меньшим приоритетом, независимо от времени их добавления.
Особого внимания заслуживает ситуация с одинаковыми приоритетами. Когда два или более элементов имеют идентичное значение важности, Priority Queue возвращается к классическому принципу FIFO — такие объекты обслуживаются в порядке их поступления. Эта логика обеспечивает предсказуемость поведения структуры и исключает неопределённость в граничных случаях.
Сравнение порядка обработки:
FIFO (обычная очередь):
- Добавлены элементы: A → B → C → D.
- Порядок извлечения: A → B → C → D.
- Время добавления — единственный критерий.
Priority Queue:
- Добавлены элементы: (A, приоритет 2) → (B, приоритет 5) → (C, приоритет 1) → (D, важность 5).
- Порядок извлечения: B → D → A → C.
- Приоритет — основной критерий, время добавления — вторичный (для B и D применён FIFO).
Ключевое свойство, которое часто упускается: Priority Queue гарантирует доступ к элементу с максимальным приоритетом за константное время при правильной реализации (операция peek), но вставка и удаление требуют логарифмического времени для поддержания внутренней структуры.
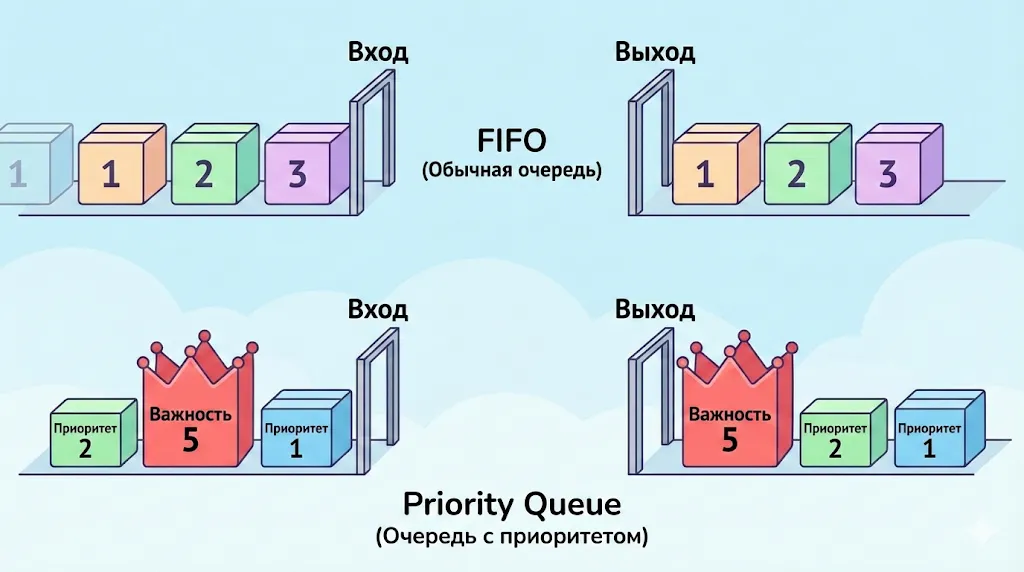
В обычной очереди (FIFO) элементы обслуживаются в порядке поступления. В очереди с приоритетом элемент с наивысшей важностью всегда извлекается первым
Типы очередей с приоритетом: min-priority и max-priority
Очереди с приоритетом существуют в двух основных вариантах, которые определяют, какой элемент считается приоритетным: min-priority queue и max-priority queue. Различие между ними заключается в интерпретации значения важности и, соответственно, в правилах извлечения объектов.
Min-priority queue (минимальная куча)
В очереди с минимальным приоритетом элементы с меньшими числовыми значениями считаются более приоритетными. Корень структуры всегда содержит запись с наименьшим значением, и именно она извлекается первой при операции удаления. Представим очередь с элементами 4, 6, 8, 9, 10 — первым будет извлечён объект 4, как имеющий минимальное значение.
Этот тип находит применение в задачах, где важны минимальные характеристики: поиск кратчайшего пути (алгоритм Дейкстры), построение минимального остовного дерева (алгоритм Прима), планирование задач с минимальным временем выполнения.
Max-priority queue (максимальная куча)
В очереди с максимальным приоритетом, напротив, элементы с большими числовыми значениями имеют более высокую важность. Корневой элемент структуры — это максимальное значение, и операция извлечения всегда возвращает наибольший объект. Для той же последовательности 4, 6, 8, 9, 10 первым будет извлечена запись 10.
Такой подход используется в системах, где требуется обработка наиболее значимых элементов: планировщики процессов с высоким приоритетом, системы обработки событий, где его важность определяется «весом», алгоритмы выбора оптимальных решений.
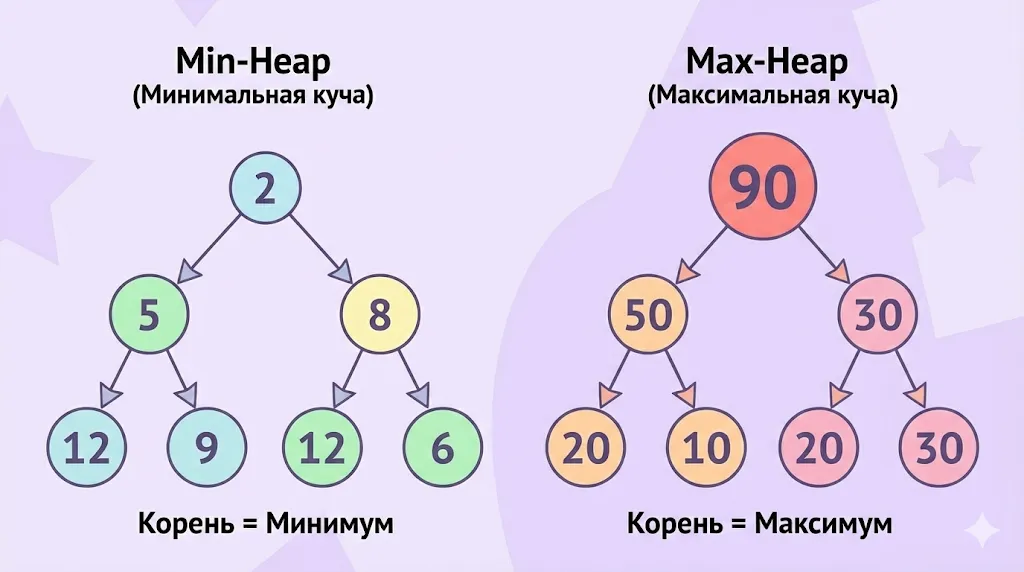
В Min-Heap корень всегда содержит минимальный элемент, а в Max-Heap — максимальный. Выбор типа зависит от задачи: поиск минимума или максимума.
Сравнение типов:
- Min-priority: извлекает минимум, применяется для оптимизационных задач на минимум.
- Max-priority: извлекает максимум, применяется для задач с явной иерархией важности.
- Правило извлечения: min → heap[0] содержит min, max → heap[0] содержит max.
- Оба типа поддерживают идентичные операции с одинаковой сложностью.
Важно понимать, что выбор между min и max — это вопрос семантики конкретной задачи, а не технических ограничений: любую min-priority queue можно превратить в max-priority, инвертировав значения важности.
Основные операции Priority Queue
Priority Queue как абстрактный тип данных поддерживает набор операций, которые обеспечивают корректную работу с приоритезированными элементами. Рассмотрим каждую из них подробнее, уделяя внимание не только синтаксису, но и внутренней логике выполнения.
Insert / Add — вставка элемента
Операция вставки добавляет новый объект в очередь с учётом его приоритета. Процесс не сводится к простому добавлению в конец структуры — после вставки необходимо восстановить свойство кучи (heap property), чтобы гарантировать корректный порядок записей.
Логика вставки:
- Новый элемент размещается в первой свободной позиции (конец массива или последний уровень дерева).
- Запускается процесс «всплытия» (heapify-up): запись сравнивается со своим родителем.
- Если приоритет нового объекта выше родительского, они меняются местами.
- Процесс повторяется до тех пор, пока элемент не займёт правильную позицию или не достигнет корня.
Временная сложность вставки составляет O(log n), поскольку в худшем случае объект может «всплыть» от листа до корня, проходя высоту дерева.
Peek / Top — просмотр элемента с максимальным приоритетом
Эта операция возвращает запись с наивысшей важностью, не удаляя её из очереди. В правильно организованной Priority Queue этот объект всегда находится в корне структуры (индекс 0 при массивном представлении), что обеспечивает доступ за константное время O(1).
Операция peek критически важна в сценариях, где требуется проверить приоритетную запись без изменения состояния очереди — например, при анализе условий для принятия решения о дальнейшей обработке.
Pop / Remove — извлечение элемента с максимальным приоритетом
Операция извлечения удаляет и возвращает объект с наивысшим приоритетом. Это наиболее сложная операция с точки зрения поддержания структурной целостности.
Схема извлечения:
- Сохранить корневой элемент для возврата.
- Заменить корень последней записью в структуре (последний лист дерева).
- Удалить последний элемент.
- Запустить процесс «погружения» (heapify-down):
- Сравнить текущий объект с его потомками.
- Выбрать потомка с наивысшей важностью.
- Если приоритет потомка выше, поменять элементы местами.
- Повторять до восстановления свойства кучи или достижения листа.
Временная сложность извлечения также составляет O(log n), так как запись может «погрузиться» на всю высоту дерева.
Дополнительные операции (isEmpty, size, update priority)
Помимо основных операций, Priority Queue часто поддерживает вспомогательные методы:
isEmpty() — проверка пустоты очереди, выполняется за O(1), критична для предотвращения ошибок при попытке извлечения из пустой структуры.
size() — возвращает количество элементов в очереди за O(1), если размер хранится как отдельное поле.
update priority — изменение важности существующей записи. Эта операция требует поиска объекта O(n) и последующего восстановления свойства кучи O(log n), что даёт общую сложность O(n). В некоторых реализациях для оптимизации используются дополнительные хеш-таблицы, сокращающие время поиска.
Список всех операций с временной сложностью:
- insert(element, priority): O(log n).
- peek() / top(): O(1).
- pop() / remove(): O(log n).
- isEmpty(): O(1).
- size(): O(1).
- update(element, new_priority): O(n) или O(log n) с индексацией.
Понимание сложности операций позволяет принимать обоснованные решения при проектировании алгоритмов, особенно когда речь идёт о больших объёмах данных и требованиях к производительности.
| Операция | Что делает | Временная сложность | Почему так быстро / медленно |
| insert | Добавляет элемент с приоритетом | O(log n) | Требуется восстановить свойство кучи (heapify-up) |
| peek / top | Возвращает самый приоритетный элемент | O(1) | Элемент всегда находится в корне кучи |
| pop / remove | Удаляет и возвращает приоритетный элемент | O(log n) | После удаления нужно выполнить heapify-down |
| isEmpty | Проверяет, пуста ли очередь | O(1) | Хранится текущее количество элементов |
| size | Возвращает число элементов | O(1) | Размер поддерживается как отдельное поле |
| update priority | Изменяет приоритет существующего элемента | O(n) / O(log n)* | Нужно найти элемент, затем восстановить кучу |
Реализации очереди с приоритетом: от простых до эффективных
Priority Queue можно реализовать различными способами, каждый из которых имеет свои преимущества и ограничения. Выбор конкретной реализации зависит от требований к производительности, объёма данных и специфики задачи. Давайте рассмотрим основные подходы — от наиболее простых до оптимальных.
Реализация на массиве (unsorted / sorted array)
Неупорядоченный массив представляет собой простейший подход: записи добавляются в конец массива без какой-либо сортировки. Вставка выполняется за O(1) — мы просто помещаем объект в следующую свободную позицию. Однако при извлечении приходится сканировать весь массив для поиска записи с максимальной важностью, что даёт O(n). Операция peek также требует полного просмотра — O(n).
Упорядоченный массив инвертирует соотношение сложностей: массив постоянно поддерживается в отсортированном состоянии. Извлечение и просмотр становятся тривиальными — O(1), поскольку запись с наивысшим приоритетом всегда находится на известной позиции (начало или конец массива). Но вставка теперь требует O(n) времени: необходимо найти правильную позицию и сдвинуть все последующие элементы.
Массивные реализации подходят для небольших очередей или случаев, когда одна из операций выполняется значительно чаще других.
Реализация на связанном списке
Связанный список предлагает альтернативу массивам, избегая необходимости перемещения элементов при вставке. В неупорядоченном списке вставка выполняется за O(1) — добавляем в голову или хвост. Извлечение и просмотр требуют линейного поиска — O(n).
Упорядоченный связанный список позволяет выполнять извлечение за O(1), но вставка требует O(n) для поиска правильной позиции. Преимущество перед упорядоченным массивом незначительно: мы экономим на сдвиге записей, но всё равно тратим линейное время на обход.
Связанные списки целесообразны, когда важна экономия памяти при динамическом изменении размера или когда требуется избежать перераспределения памяти, характерного для массивов.
Реализация через бинарное дерево поиска
Бинарное дерево поиска (BST) предлагает более гармоничный подход. В идеальном случае — при сбалансированном дереве — все операции (вставка, извлечение, поиск) выполняются за O(log n). Запись с максимальным приоритетом находится в самом правом узле дерева (для max-heap) или в самом левом (для min-heap).
Однако BST имеет существенный недостаток: в худшем случае, когда элементы добавляются в отсортированном порядке, дерево вырождается в связанный список, и все операции деградируют до O(n). Для предотвращения этого требуются самобалансирующиеся варианты (AVL-дерево, красно-чёрное дерево), что значительно усложняет реализацию.
Реализация на двоичной куче (binary heap)
Двоичная куча — это стандарт де-факто для реализации Priority Queue, и на то есть веские причины. Структура представляет собой полное бинарное дерево, хранящееся в массиве, что обеспечивает компактность и cache-friendly доступ к данным.
Ключевые преимущества binary heap:
- Гарантированная сложность O(log n) для вставки и удаления в любом случае.
- Константное время O(1) для доступа к максимальной записи.
- Эффективное использование памяти благодаря массивному хранению.
- Простота реализации по сравнению с балансирующимися деревьями.
- Отсутствие накладных расходов на указатели (как в связанных структурах).
Структура кучи автоматически поддерживается как полное дерево минимальной высоты, что исключает вырождение. Индексация через формулы (parent: (i-1)/2, left child: 2i+1, right child: 2i+2) обеспечивает прямой доступ к узлам без необходимости хранения указателей.
Сравнительная таблица временных сложностей:
| Реализация | Insert | Peek | Remove |
| Неупорядоченный массив | O(1) | O(n) | O(n) |
| Упорядоченный массив | O(n) | O(1) | O(1) |
| Неупорядоченный список | O(1) | O(n) | O(n) |
| Упорядоченный список | O(n) | O(1) | O(1) |
| BST (сбалансированное) | O(log n) | O(log n) | O(log n) |
| BST (худший случай) | O(n) | O(n) | O(n) |
| Binary Heap | O(log n) | O(1) | O(log n) |
Преимущества и недостатки основных подходов:
- Массивы: простота реализации, но низкая эффективность при больших объёмах; подходят для статических или малых очередей.
- Связанные списки: динамическое управление памятью, но накладные расходы на указатели и плохая локальность данных; редко используются на практике.
- BST: универсальность структуры, но сложность балансировки и риск деградации; требуют дополнительной логики для поддержания эффективности.
- Binary Heap: оптимальный баланс между производительностью и простотой; стандартный выбор для промышленных реализаций Priority Queue.
Именно поэтому большинство библиотечных реализаций — от std::priority_queue в C++ до heapq в Python и PriorityQueue в Java — используют binary heap как базовую структуру данных.
Как работает бинарная куча в Priority Queue
Бинарная куча заслуживает детального рассмотрения как наиболее эффективная и широко применяемая реализация Priority Queue. Понимание внутренних механизмов этой структуры позволяет не только использовать её корректно, но и оптимизировать алгоритмы в критических по производительности сценариях.
Структура binary heap и массивное хранение
Бинарная куча представляет собой полное бинарное дерево — структуру, в которой все уровни, кроме возможно последнего, полностью заполнены, а последний заполняется слева направо. Это свойство критически важно: оно гарантирует минимальную высоту дерева и позволяет эффективно хранить структуру в обычном массиве без использования указателей.
Массивное представление основано на математических соотношениях между индексами записей. Для элемента с индексом i:
- Родительский узел находится по индексу (i — 1) / 2.
- Левый потомок находится по индексу 2 * i + 1.
- Правый потомок находится по индексу 2 * i + 2.
Корень дерева всегда расположен в позиции 0. Это элегантное решение позволяет навигировать по дереву через простые арифметические операции, избегая накладных расходов на хранение и разыменование указателей. Кроме того, последовательное расположение данных в памяти обеспечивает высокую эффективность кэширования процессора.
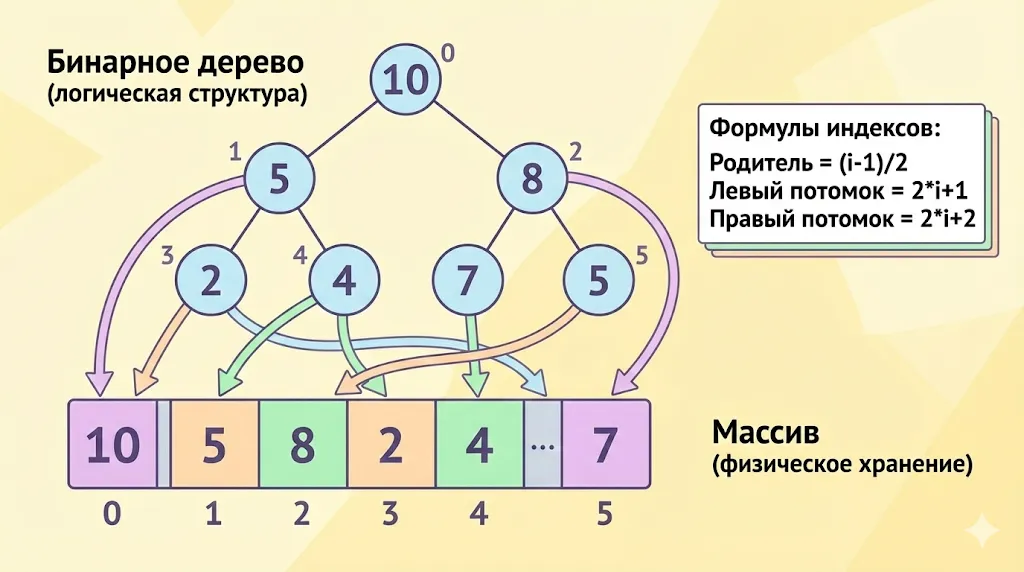
Отображение бинарного дерева в массив.
Бинарная куча логически представляет собой дерево, но физически хранится в массиве. Навигация между узлами осуществляется с помощью простых арифметических операций над индексами.
Основное свойство кучи (heap property): значение каждого узла должно быть больше или равно (для max-heap) либо меньше или равно (для min-heap) значениям всех его потомков. Это свойство распространяется рекурсивно на всё дерево и обеспечивает нахождение записи с экстремальной важностью в корне.
Алгоритм вставки (heapify-up)
Процесс вставки нового объекта состоит из двух этапов: размещения и восстановления свойства кучи.
Шаги алгоритма heapify-up:
- Добавить новый элемент в конец массива (первая свободная позиция на последнем уровне дерева).
- Сравнить добавленную запись с её родителем по индексу (i — 1) / 2.
- Если приоритет нового объекта выше родительского (для max-heap), поменять их местами.
- Повторять шаг 2-3 для новой позиции элемента, пока он не достигнет корректной позиции или не станет корнем.
- Завершить процесс, когда свойство кучи восстановлено.
Этот процесс называется «всплытием» записи. В худшем случае объект проходит путь от последнего уровня до корня, что соответствует высоте дерева — отсюда логарифмическая сложность O(log n). На практике большинство элементов «всплывают» лишь на несколько уровней, что делает среднюю производительность ещё лучше.
Алгоритм удаления (heapify-down)
Извлечение корневого элемента требует более сложной процедуры восстановления структуры, поскольку необходимо заполнить освободившуюся позицию и реорганизовать дерево.
Шаги алгоритма heapify-down:
- Сохранить значение корня (индекс 0) для возврата
- Заменить корень последней записью массива
- Удалить последний элемент (уменьшить размер массива)
- Начать процесс «погружения» с корня:
- Определить индексы левого (2 * i + 1) и правого (2 * i + 2) потомков
- Выбрать потомка с наивысшей важностью
- Если приоритет текущего объекта ниже выбранного потомка, поменять их местами
- Перейти к позиции потомка и повторить процесс
- Завершить, когда элемент достигнет позиции, где свойство кучи восстановлено, или станет листом
- Вернуть сохранённое значение корня
Важная деталь: при наличии обоих потомков необходимо выбирать для обмена того, у которого важность выше (для max-heap). Это гарантирует, что после обмена свойство кучи будет выполняться относительно обоих потомков.
Временная сложность операции также составляет O(log n), поскольку запись может «погрузиться» на всю высоту дерева.
Почему binary heap — оптимальный выбор
Превосходство бинарной кучи над альтернативными реализациями обусловлено несколькими факторами, которые в совокупности создают оптимальное решение для большинства практических задач.
- Гарантированная производительность. Binary heap обеспечивает логарифмическую сложность основных операций в любом сценарии — нет худших случаев с деградацией до линейного времени, как у несбалансированных BST. Константное время доступа к экстремальной записи делает структуру идеальной для алгоритмов, требующих частых операций peek.
- Эффективность использования памяти. Массивное хранение полного дерева не требует дополнительной памяти на указатели. Для n элементов используется ровно n ячеек массива плюс несколько служебных переменных. Сравните с BST, где каждый узел хранит минимум два указателя, увеличивая потребление памяти на 200-300%.
- Локальность данных. Последовательное расположение записей в массиве обеспечивает эффективную работу процессорного кэша. При обходе дерева вниз или вверх соседние объекты часто находятся в одной кэш-линии, что минимизирует промахи кэша и ускоряет выполнение операций.
- Простота реализации и сопровождения. Алгоритмы heapify-up и heapify-down концептуально просты и требуют минимального количества кода. Отсутствие сложной логики балансировки, характерной для AVL или красно-чёрных деревьев, снижает вероятность ошибок и упрощает отладку.
Именно эта совокупность качеств объясняет, почему binary heap стала стандартом для реализации Priority Queue в промышленных библиотеках и продолжает оставаться первым выбором разработчиков при проектировании систем с приоритезацией данных.
Примеры кода реализации Priority Queue
Рассмотрим практические реализации Priority Queue на наиболее популярных языках программирования. Каждый язык предлагает свои подходы к работе с приоритетными очередями — от встроенных библиотечных решений до возможности создания собственных реализаций.
Python
Python предоставляет модуль heapq, который реализует min-heap. Важная особенность: по умолчанию это минимальная куча, поэтому для создания max-heap требуется инвертировать значения важности.
import heapq
# Создание priority queue (min-heap)
pq = []
# Вставка элементов (приоритет, значение)
heapq.heappush(pq, (1, "задача с низким приоритетом"))
heapq.heappush(pq, (5, "срочная задача"))
heapq.heappush(pq, (3, "средняя задача"))
# Извлечение элемента с минимальным приоритетом
priority, task = heapq.heappop(pq)
print(f"Обработка: {task} (приоритет {priority})")
# Просмотр без удаления
if pq:
print(f"Следующая задача: {pq[0]}")
# Для max-heap инвертируем приоритеты
max_pq = []
heapq.heappush(max_pq, (-5, "высокий приоритет"))
heapq.heappush(max_pq, (-1, "низкий приоритет"))
Особенности Python-реализации:
- Встроенный модуль работает только с min-heap.
- Для max-heap используется трюк с отрицательными значениями важности.
- Операции выполняются непосредственно над списком.
- Поддержка кортежей позволяет естественно хранить пары (приоритет, данные).
Java
Java предлагает класс PriorityQueue из пакета java.util, который по умолчанию создаёт min-heap, но позволяет настроить компаратор для изменения порядка.
import java.util.PriorityQueue;
import java.util.Collections;
public class PriorityQueueExample {
public static void main(String[] args) {
// Min-heap (по умолчанию)
PriorityQueue minPQ = new PriorityQueue<>();
minPQ.add(10);
minPQ.add(30);
minPQ.add(20);
minPQ.add(5);
System.out.println("Минимальный элемент: " + minPQ.peek()); // 5
System.out.println("Извлечение: " + minPQ.poll()); // 5
// Max-heap с использованием компаратора
PriorityQueue maxPQ = new PriorityQueue<>(Collections.reverseOrder());
maxPQ.add(10);
maxPQ.add(30);
maxPQ.add(20);
System.out.println("Максимальный элемент: " + maxPQ.peek()); // 30
// Priority Queue с пользовательскими объектами
PriorityQueue taskQueue = new PriorityQueue<>(
(t1, t2) -> Integer.compare(t2.priority, t1.priority)
);
taskQueue.add(new Task("Задача А", 3));
taskQueue.add(new Task("Задача Б", 1));
taskQueue.add(new Task("Задача В", 5));
while (!taskQueue.isEmpty()) {
System.out.println(taskQueue.poll());
}
}
}
class Task {
String name;
int priority;
Task(String name, int priority) {
this.name = name;
this.priority = priority;
}
@Override
public String toString() {
return name + " (приоритет: " + priority + ")";
}
}
Особенности Java-реализации:
- Гибкая настройка через компараторы.
- Типобезопасность благодаря generics.
- Методы peek(), poll(), add() соответствуют стандартным операциям.
- Поддержка пользовательских объектов с кастомной логикой сравнения.
C++
C++ предоставляет шаблонный класс std::priority_queue из библиотеки STL, который по умолчанию создаёт max-heap.
#include
#include
#include
int main() {
// Max-heap (по умолчанию)
std::priority_queue maxPQ;
maxPQ.push(10);
maxPQ.push(30);
maxPQ.push(20);
maxPQ.push(5);
std::cout << "Максимальный элемент: " << maxPQ.top() << std::endl; // 30
maxPQ.pop();
std::cout << "После удаления: " << maxPQ.top() << std::endl; // 20
// Min-heap с использованием greater
std::priority_queue<int, std::vector, std::greater> minPQ;
minPQ.push(10);
minPQ.push(30);
minPQ.push(20);
std::cout << "Минимальный элемент: " << minPQ.top() << std::endl; // 10
// Priority Queue с парами (приоритет, данные)
std::priority_queue<std::pair<int, std::string>> taskQueue;
taskQueue.push({3, "Средняя задача"});
taskQueue.push({1, "Низкий приоритет"});
taskQueue.push({5, "Срочная задача"});
while (!taskQueue.empty()) {
auto task = taskQueue.top();
std::cout << task.second << " (приоритет: " << task.first << ")" << std::endl;
taskQueue.pop();
}
return 0;
}
Особенности C++-реализации:
- По умолчанию создаёт max-heap (в отличие от Python и Java).
- Шаблонная природа позволяет работать с любыми типами.
- Параметризация через компараторы (std::greater для min-heap).
- Высокая производительность благодаря отсутствию накладных расходов на виртуальные вызовы.
Все три языка предоставляют эффективные реализации на основе binary heap, гарантирующие логарифмическую сложность основных операций. Выбор конкретного языка определяется требованиями проекта, но концептуально работа с Priority Queue остаётся идентичной: вставка с учётом важности, извлечение объекта с максимальным или минимальным приоритетом, просмотр без удаления.
Где применяется Priority Queue — практические сценарии
Priority Queue находит широкое применение как в классических алгоритмах теории графов и обработки данных, так и в реальных системах, где требуется управление задачами с различными уровнями важности. Рассмотрим ключевые области использования этой структуры данных.
Алгоритм Дейкстры
Алгоритм Дейкстры для поиска кратчайшего пути в графе с неотрицательными весами рёбер является классическим примером эффективного использования Priority Queue. На каждой итерации алгоритм должен выбирать вершину с минимальным текущим расстоянием от стартовой точки — именно здесь min-priority queue становится критически важной.
Без приоритетной очереди пришлось бы каждый раз сканировать все непосещённые вершины для поиска минимума, что дало бы сложность O(V²). С использованием binary heap сложность снижается до O((V + E) log V), где V — количество вершин, E — количество рёбер. Для разреженных графов, где E значительно меньше V², это даёт существенное ускорение.
Пример задачи: поиск оптимального маршрута в навигационных системах, где вершины — это перекрёстки, рёбра — дороги, а веса — время или расстояние.
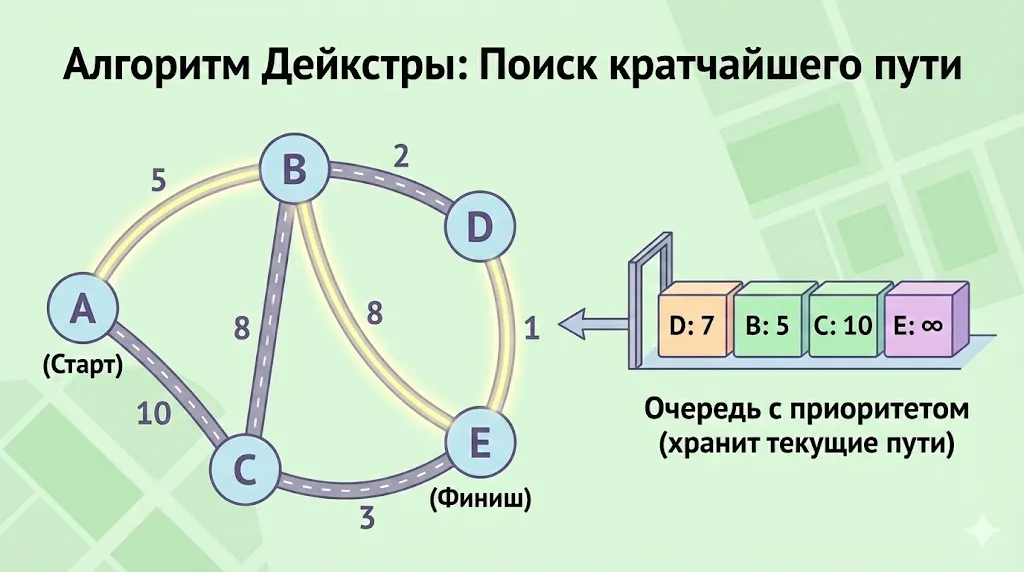
Priority Queue используется в алгоритме Дейкстры для эффективного выбора вершины с минимальным текущим расстоянием, что позволяет быстро находить кратчайший путь в графе.
Алгоритм Прима
Алгоритм Прима для построения минимального остовного дерева также опирается на Priority Queue. Структура хранит рёбра, упорядоченные по весу, и на каждом шаге алгоритм извлекает ребро с минимальным весом, соединяющее уже построенное дерево с новой вершиной.
Использование min-heap обеспечивает эффективность O(E log V), что делает алгоритм применимым для больших графов. Без приоритетной очереди каждое извлечение минимального ребра потребовало бы линейного поиска, увеличивая общую сложность до O(V · E).
Пример задачи: проектирование сетевой инфраструктуры с минимальной общей стоимостью кабелей, соединяющих все узлы корпоративной сети.
Кодирование Хаффмана
Алгоритм Хаффмана для построения оптимального префиксного кода использует Priority Queue для хранения узлов дерева, упорядоченных по частоте встречаемости символов. На каждом шаге извлекаются два узла с минимальной частотой, объединяются в новый узел, который помещается обратно в очередь.
Min-heap позволяет эффективно находить наименее частотные записи за O(log n) вместо линейного поиска. Общая сложность построения дерева Хаффмана составляет O(n log n), где n — количество уникальных символов.
Пример задачи: сжатие текстовых данных или изображений, где часто встречающиеся символы кодируются короткими битовыми последовательностями.
Планировщики задач (CPU scheduling)
В операционных системах Priority Queue используется для управления выполнением процессов. Каждый процесс имеет уровень важности, определяющий его приоритетность выполнения. Планировщик извлекает из очереди процесс с наивысшей значимостью и выделяет ему процессорное время.
Различные стратегии планирования опираются на приоритетные очереди:
- Статические приоритеты: критические системные процессы всегда обрабатываются раньше пользовательских приложений.
- Динамические приоритеты: важность процесса изменяется в зависимости от времени ожидания или потребления ресурсов.
- Многоуровневые очереди: несколько Priority Queue с различными политиками для разных классов задач.
Пример задачи: серверная система обработки запросов, где платные пользователи получают более высокую важность обслуживания по сравнению с бесплатными аккаунтами.
Другие практические применения
- Симуляция событий. В дискретно-событийном моделировании Priority Queue хранит будущие события, упорядоченные по времени наступления. Это позволяет эффективно обрабатывать события в хронологическом порядке без необходимости постоянной сортировки всего массива.
- Медианный фильтр в обработке сигналов. Две Priority Queue (max-heap и min-heap) используются для эффективного вычисления скользящей медианы в потоке данных — задаче, критичной для обработки изображений и звука.
- Управление памятью. В системах с ограниченными ресурсами Priority Queue помогает определять, какие объекты следует выгрузить из кэша или удалить из памяти, основываясь на их важности и частоте использования.
- Сетевая маршрутизация. Протоколы маршрутизации используют приоритетные очереди для управления порядком передачи пакетов, обеспечивая более высокую важность критичным данным (например, VoIP-трафику) над менее чувствительными к задержкам (загрузка файлов).
Возникает вопрос: что объединяет все эти разнородные применения? Ответ прост — в каждом случае система должна эффективно выбирать «наиболее важный» объект из динамически изменяющегося набора, и именно Priority Queue предоставляет оптимальное решение этой задачи с гарантированной производительностью.
Преимущества и ограничения очередей с приоритетом
Как и любая структура данных, Priority Queue имеет свои сильные стороны и ситуации, в которых её использование может быть неоптимальным. Понимание этих аспектов позволяет принимать обоснованные архитектурные решения при проектировании систем.
Преимущества
- Гарантированная эффективность основных операций. Binary heap обеспечивает O(log n) для вставки и удаления при O(1) для доступа к экстремальной записи, что делает структуру предсказуемой и надёжной даже при больших объёмах данных.
- Автоматическое поддержание порядка. В отличие от массивов или списков, где сортировка требует явных действий, Priority Queue самостоятельно поддерживает необходимый порядок объектов после каждой операции модификации.
- Компактность и эффективность памяти. Массивная реализация binary heap не требует дополнительной памяти на указатели, обеспечивая оптимальное использование ресурсов и хорошую локальность данных для процессорного кэша.
- Естественное решение для задач с приоритетами. Структура идеально подходит для сценариев, где требуется постоянный доступ к «наиболее важному» объекту — от алгоритмов на графах до планирования задач в реальном времени.
- Простота интеграции. Наличие готовых библиотечных реализаций в большинстве языков программирования снижает порог входа и минимизирует риск ошибок в собственных реализациях.
Ограничения
- Отсутствие эффективного поиска произвольных элементов. Priority Queue оптимизирована для работы с экстремальной записью, но поиск или удаление объекта по значению требует O(n) времени. Если задача требует частого доступа к записям по ключу, следует рассмотреть хеш-таблицы или сбалансированные деревья поиска.
- Сложность обновления приоритетов. Изменение важности существующего объекта — операция нетривиальная: необходимо найти запись O(n), а затем восстановить свойство кучи O(log n). Некоторые задачи (например, вариации алгоритма Дейкстры) требуют частых обновлений, что может снижать общую эффективность.
- Ограниченная функциональность стандартных реализаций. Библиотечные Priority Queue обычно не поддерживают операции вроде decrease-key (уменьшение важности) или произвольного удаления записи, что вынуждает разработчиков создавать расширенные версии для специфических задач.
- Невозможность эффективной итерации в отсортированном порядке. Обход элементов Priority Queue не гарантирует их следование в порядке приоритетов — для получения отсортированного списка необходимо последовательно извлекать все записи, разрушая структуру.
- Накладные расходы при малых объёмах данных. Для очередей из 5-10 элементов поддержание структуры кучи может оказаться избыточным — простой упорядоченный массив с линейным поиском может работать быстрее благодаря меньшим константным факторам и лучшей предсказуемости для процессора.
Когда Priority Queue — неподходящий выбор? Если задача требует частого доступа к записям по ключу, необходима полная сортировка всех объектов, критична операция поиска середины диапазона или нужна поддержка сложных запросов (например, «найти все элементы с приоритетом выше X») — в таких случаях стоит рассмотреть альтернативные структуры: сбалансированные деревья, skip-списки или специализированные индексы.
Однако для задач, где доминируют операции «добавить элемент» и «извлечь наиболее приоритетную запись», Priority Queue остаётся оптимальным и элегантным решением, проверенным десятилетиями использования в критически важных алгоритмах и системах.
Заключение
В этой статье мы рассмотрели Priority Queue — структуру данных, которая играет ключевую роль в современных алгоритмах и системах управления ресурсами. От базового определения и принципов работы до детального анализа реализации на binary heap, мы прошли путь от теории к практическому применению. Подведем итоги:
- Очередь с приоритетом это структура данных, где порядок обработки определяется важностью элементов. Это делает её эффективной для задач с разным уровнем срочности.
- Ключевое отличие от fifo заключается в том, что приоритет важнее времени добавления. При равных значениях сохраняется принцип очереди.
- Наиболее эффективная реализация основана на бинарной куче. Она обеспечивает баланс между скоростью и экономией памяти.
- Основные операции имеют логарифмическую сложность, а доступ к приоритетному элементу выполняется за константное время. Это критично для производительных систем.
- Структура активно используется в алгоритмах дейкстры, прима и хаффмана. Также она применяется в планировщиках задач и сетевых системах.
- Несмотря на преимущества, очередь с приоритетом неудобна для поиска произвольных элементов. Это важно учитывать при проектировании алгоритмов.
Если вы только начинаете осваивать разработчика, рекомендуем обратить внимание на подборку курсов по разработке на Python. В программах обучения обычно есть теоретическая и практическая часть, что помогает лучше понять структуры данных и их применение в реальных задачах.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
1 февраля
|
Подробнее |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 марта
|
Подробнее |
|
Fullstack-разработчик на Python
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
175 800 ₽
308 367 ₽
|
От
5 139 ₽/мес
|
Длительность
18 месяцев
|
Старт
12 февраля
|
Подробнее |
|
Python-разработчик
|
Академия Синергия
35 отзывов
|
Цена
Ещё -5% по промокоду
89 800 ₽
|
От
3 742 ₽/мес
0% на 24 месяца
|
Длительность
6 месяцев
|
Старт
3 февраля
|
Подробнее |
|
Профессия Python-разработчик
|
Skillbox
218 отзывов
|
Цена
Ещё -20% по промокоду
74 507 ₽
149 015 ₽
|
От
6 209 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
3 февраля
|
Подробнее |

Как измерить эффективность контент-маркетинга: полное руководство
Эффективность контент-маркетинга — это не только цифры, но и понимание, как они влияют на бизнес. В статье вы узнаете, как анализировать ключевые метрики, использовать UTM-метки и внедрять data-driven подход для оптимизации контент-стратегии.
Календарный план проекта — что это и как правильно его составить
Без чёткого плана даже самый перспективный проект рискует превратиться в хаос. Календарный план проекта — это инструмент, который помогает организовать задачи по времени, расставить приоритеты и избежать дедлайнов в духе «вчера». В этой статье вы узнаете, что такое календарный план, из чего он состоит, зачем нужен и как его грамотно составить, чтобы проект шёл по графику, а не по наитию.

Конфигурационное тестирование: полное руководство по проверке совместимости программного обеспечения
Тестирование конфигурации — важный этап проверки программного обеспечения перед релизом. Как понять, какие окружения действительно нужно тестировать и где чаще всего скрываются ошибки совместимости? В статье разберём практические подходы и типичные сценарии.

Деструкторы в Python: что это, как работают и когда их использовать
Деструктор в Python часто воспринимают как простой способ освободить ресурсы, но так ли это на самом деле? В статье разбираемся, когда __del__() действительно работает, где он опасен и какие решения лучше использовать на практике.