Округление чисел в JavaScript: полный разбор всех методов и примеров
На первый взгляд, округление кажется простейшей операцией — просто убрать всё после запятой и готово. Однако в реальной практике веб-разработки мы сталкиваемся с гораздо более сложными сценариями, где правильный выбор метода округления может определить корректность работы всего приложения.

Давайте рассмотрим типовые задачи, где округление становится критически важным:
- Финансовые расчёты. Когда мы работаем с денежными суммами, каждая копейка имеет значение. Неправильное округление при расчёте скидок, налогов или комиссий может привести к расхождениям в бухгалтерии или потере доверия пользователей.
- Отображение данных в интерфейсе. Показывать пользователю число вроде 3.14159265359 — не лучшая идея. Для UI нужны читаемые значения: 3.14 для визуализации графиков, округлённые проценты для прогресс-баров.
- Работа с координатами и позиционированием. Хотя CSS поддерживает дробные пиксели, в некоторых случаях (например, при отрисовке тонких линий на Canvas или для идеальной четкости текста/границ) округление помогает попасть в физическую сетку пикселей и избежать эффекта размытия (anti-aliasing).
- Оптимизация вычислений. В играх и анимациях, где производительность критична, округление помогает работать с целочисленными значениями вместо дробных, что ускоряет расчёты.
- Как устроены числа в JavaScript и почему возникают ошибки точности
- Объект Math в JavaScript: зачем он нужен
- Основные методы округления в JS: полный разбор с примерами
- Как методы округления ведут себя с разными типами данных
- Как округлить число до нужного количества знаков после запятой
- Практические примеры использования округления
- Типичные ошибки при округлении в JavaScript и как их избежать
- Заключение
- Рекомендуем посмотреть курсы по JavaScript разработке
Как устроены числа в JavaScript и почему возникают ошибки точности
Прежде чем разбираться с методами округления, важно понять, как JavaScript вообще работает с числами. Именно здесь кроется корень большинства проблем, с которыми сталкиваются разработчики.
В JavaScript существует основной числовой тип Number, который охватывает как целые, так и дробные числа. Казалось бы, всё просто — но на практике этот тип таит в себе неожиданности. Дело в том, что JavaScript использует стандарт IEEE 754 для хранения чисел с плавающей точкой двойной точности. Это означает, что числа хранятся в двоичной системе, а не в привычной нам десятичной.
Как это работает технически: число разбивается на три компонента — знак (плюс или минус), мантиссу (значащие цифры) и экспоненту (порядок числа). Вся эта информация упаковывается в 64 бита. Диапазон чисел впечатляет — примерно от -9 до +9 квадриллионов, но вот точность хранения дробной части ограничена.
Именно здесь начинаются сюрпризы. Некоторые десятичные дроби, которые кажутся простыми (например, 0.1), не могут быть точно представлены в двоичной системе — подобно тому, как 1/3 в десятичной системе превращается в бесконечную дробь 0.333…
Отсюда возникает классический пример, который озадачивает всех новичков:
0.1 + 0.2 // Результат: 0.30000000000000004
Мы ожидаем увидеть 0.3, но получаем число с длинным хвостом. Это не баг JavaScript — так работает арифметика с плавающей точкой во всех языках программирования, использующих этот стандарт.
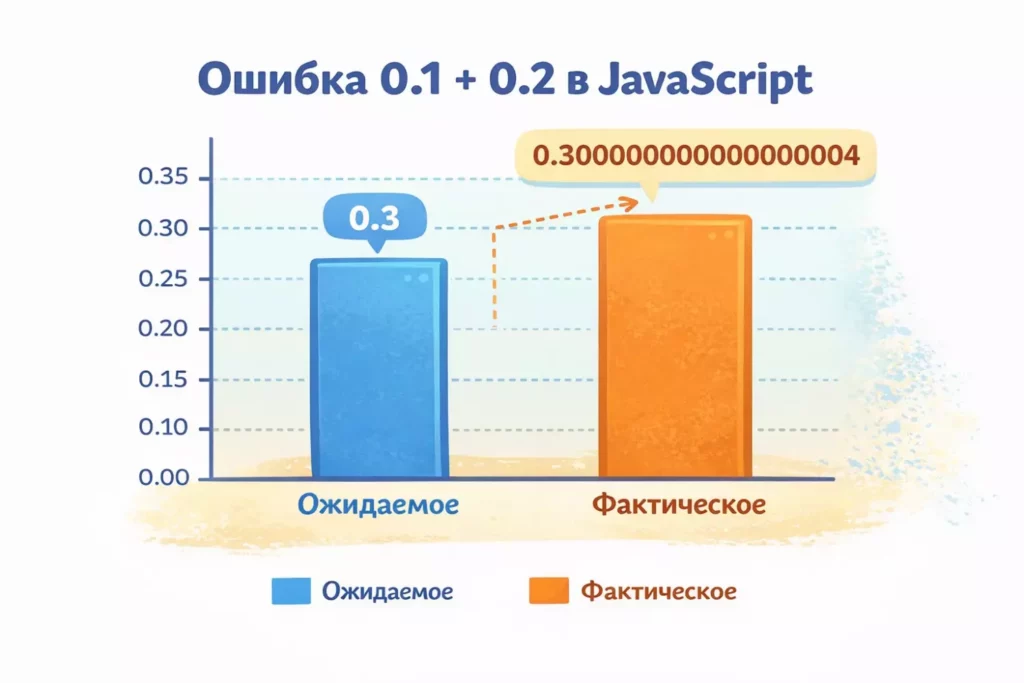
Диаграмма показывает расхождение между ожидаемым результатом вычисления и фактическим значением, которое возвращает JavaScript. Ошибка возникает из-за особенностей представления дробных чисел в двоичной системе. Это не баг языка, а следствие стандарта IEEE 754.
Типичные проблемы точности, с которыми мы сталкиваемся:
- Накопление ошибок при множественных операциях — каждое вычисление добавляет микроскопическую погрешность, которая может вырасти до заметной величины.
- Сравнение дробных чисел напрямую через === часто даёт неожиданные результаты из-за этих погрешностей.
- Финансовые расчёты становятся особенно проблематичными — центы и копейки требуют абсолютной точности, которую стандартный Number не всегда обеспечивает.
- Операции с очень большими или малыми числами могут терять точность из-за ограничений мантиссы.
Вот почему округление в JavaScript — это не просто косметическая операция для красивого отображения, а необходимый инструмент для корректной работы с числами. Далее мы разберём, какие методы помогают решать эти проблемы.
Объект Math в JavaScript: зачем он нужен
Теперь, когда мы понимаем природу числовых проблем в JavaScript, возникает логичный вопрос: как с ними бороться? Именно для этого в языке существует встроенный объект Math — своеобразный математический toolkit, который предоставляет готовые методы для работы с числами.
Math — это не конструктор и не класс в привычном понимании. Мы не можем создать его экземпляр через new Math() — такая попытка вызовет ошибку. Это статический объект, который служит контейнером для математических функций и констант. Все его методы и свойства доступны напрямую через точечную нотацию.
Ключевые методы для округления, которые мы детально разберём в следующих разделах:
- Math.round() — округляет до ближайшего целого числа по классическим математическим правилам (если дробная часть >= 0.5, округление вверх, иначе — вниз).
- Math.floor() — всегда округляет вниз, к меньшему целому числу.
- Math.ceil() — всегда округляет вверх, к большему целому числу.
- Math.trunc() — просто отбрасывает дробную часть без округления.
Помимо методов округления, объект Math содержит и другие полезные инструменты: Math.abs() для получения модуля числа, Math.random() для генерации случайных значений, Math.pow() для возведения в степень, Math.sqrt() для извлечения квадратного корня, а также математические константы вроде Math.PI.
Важная особенность: все методы Math работают только с числами. Если передать строку, объект или другой тип данных, JavaScript попытается преобразовать его в число. Это поведение может привести к неожиданным результатам, которые мы подробно рассмотрим позже — понимание того, как различные типы данных взаимодействуют с методами округления, критически важно для написания надёжного кода.
Основные методы округления в JS: полный разбор с примерами
Переходим к самой практической части — детальному разбору каждого метода округления. Понимание их различий и особенностей поведения позволит выбирать правильный инструмент для конкретной задачи.
Math.round() — округление «по правилам математики»
Метод Math.round() работает так, как нас учили в школе: если дробная часть числа меньше 0.5, округление идёт вниз, если больше или равна 0.5 — вверх. Это наиболее интуитивный способ округления, который подходит для большинства повседневных задач.
Рассмотрим примеры с положительными числами:
Math.round(4.3); // 4 -- дробная часть 0.3 < 0.5, округляем вниз Math.round(4.5); // 5 -- дробная часть 0.5, округляем вверх Math.round(4.7); // 5 -- дробная часть 0.7 > 0.5, округляем вверх Math.round(8.9); // 9 Math.round(2.1); // 2
С отрицательными числами логика та же, но результат может показаться неожиданным для тех, кто не привык к математическим соглашениям:
Math.round(-4.3); // -4 -- округление к ближайшему целому Math.round(-4.5); // -4 -- внимание! Не -5, а -4 Math.round(-4.7); // -5 -- дробная часть больше 0.5 Math.round(-2.1); // -2
Особенности поведения Math.round():
- Граничный случай с 0.5 для отрицательных чисел — именно здесь многие ошибаются. -4.5 округляется до -4, а не до -5, потому что -4 ближе к нулю и является «большим» числом в математическом смысле.
- Метод принимает только один аргумент — попытка передать второй параметр (например, количество знаков после запятой) будет проигнорирована без ошибки, но и без желаемого эффекта.
- Если передать нечисловое значение, JavaScript попытается преобразовать его в число через внутренний механизм Number(), что может дать NaN при невозможности преобразования.
- Метод всегда возвращает целое число типа Number, даже если исходное значение уже было целым — это важно понимать при проверке типов.
- Math.round() идеально подходит для задач, где важна естественная точность: отображение рейтингов, подсчёт голосов, округление результатов измерений в UI.
Math.floor() — округление вниз (к меньшему целому)
Метод Math.floor() работает иначе — он всегда округляет в меньшую сторону, независимо от дробной части. Название метода говорит само за себя: «floor» означает «пол» — число как бы опускается до ближайшего целого значения вниз по числовой оси.
Для положительных чисел поведение интуитивно понятно — дробная часть просто отбрасывается:
Math.floor(4.9); // 4 Math.floor(4.1); // 4 Math.floor(4.5); // 4 Math.floor(7.999); // 7
Однако с отрицательными числами Math.floor() демонстрирует поведение, которое часто становится источником ошибок. Помните: округление идёт к меньшему целому, а для отрицательных чисел это означает движение влево по числовой оси, то есть в сторону более отрицательных значений:
Math.floor(-4.1); // -5 (не -4!) Math.floor(-4.9); // -5 Math.floor(-2.1); // -3
Наглядная таблица поведения:
| Исходное число | Math.floor() | Пояснение |
|---|---|---|
| 5.8 | 5 | Отбрасывание дробной части |
| 5.1 | 5 | Всегда вниз для положительных |
| 0.9 | 0 | Округление к меньшему целому |
| -2.1 | -3 | Движение к более отрицательному |
| -2.9 | -3 | Всегда к меньшему значению |
| -0.5 | -1 | Отрицательная сторона числовой оси |
Где Math.floor() незаменим:
- Деление с округлением вниз — классический случай, когда нужно узнать, сколько полных единиц содержится в числе. Например, вычисление количества полных дней в часах: Math.floor(73 / 24) даст 3 дня.
- Работа с индексами массивов и координатами, где нужна гарантия, что результат будет целым числом, смещённым в меньшую сторону.
- Пагинация и разбиение на страницы — когда нужно вычислить номер страницы или блока данных.
- Расчёты в сетках и таблицах верстки, где элементы должны целиком поместиться в контейнер без переполнения.
Ключевое отличие Math.floor() от других методов — предсказуемое поведение с отрицательными числами, которое следует строгому математическому правилу «к меньшему целому», а не просто «отбрасывание дробной части».
Math.ceil() — округление вверх (к большему целому)
Метод Math.ceil() — это противоположность Math.floor(). Название происходит от слова «ceiling» (потолок), и логика работы соответствует этой метафоре: число всегда «поднимается» до ближайшего целого значения вверх по числовой оси, к большему числу.
Для положительных чисел это означает увеличение до следующего целого:
Math.ceil(4.1); // 5 Math.ceil(4.9); // 5 Math.ceil(4.01); // 5 Math.ceil(7.001); // 8
С отрицательными числами Math.ceil() ведёт себя зеркально относительно Math.floor() — округление идёт к большему целому, то есть ближе к нулю:
Math.ceil(-4.9); // -4 (не -5!) Math.ceil(-4.1); // -4 Math.ceil(-2.9); // -2 Math.ceil(-0.1); // 0
Случаи, когда Math.ceil() предпочтительнее других методов:
- Расчёт необходимого количества ресурсов. Если нужно упаковать 23 товара в коробки по 5 штук, формула Math.ceil(23 / 5) даст 5 коробок — ровно столько, сколько нужно, чтобы вместить всё.
- Определение количества страниц в пагинации: при 47 элементах и 10 на страницу Math.ceil(47 / 10) вернёт 5, учитывая неполную последнюю.
- Резервирование места в памяти или на диске. Когда нужно выделить целое количество блоков для размещения данных, округление вверх гарантирует достаточный объём.
- Вычисление времени выполнения задач. Если операция занимает 3.2 секунды, но мы показываем пользователю целые секунды, Math.ceil(3.2) вернёт 4 — более честную оценку времени ожидания.
- Работа с процентами прогресса. При отображении процента загрузки округление вверх создаёт впечатление, что система работает активнее.
Важный момент: Math.ceil() и Math.floor() не являются просто противоположностями для всех чисел. Для целых оба метода возвращают одно и то же значение. Различие проявляется только когда есть дробная часть — тогда ceil увеличивает, а floor уменьшает.
Math.trunc() — усечение дробной части без округления
Метод Math.trunc() появился в JavaScript относительно недавно (в стандарте ES6) и предлагает самую прямолинейную логику из всех методов округления: он просто отбрасывает дробную часть числа, не применяя никаких правил округления. Название происходит от слова «truncate» — усекать, обрезать.
В отличие от Math.floor(), который округляет к меньшему целому, и Math.round(), учитывающего дробную часть, Math.trunc() работает предсказуемо и одинаково для положительных и отрицательных чисел:
Math.trunc(4.9); // 4 Math.trunc(4.1); // 4 Math.trunc(-4.9); // -4 Math.trunc(-4.1); // -4 Math.trunc(0.9); // 0 Math.trunc(-0.9); // 0
Ключевое отличие становится очевидным при работе с отрицательными числами. Давайте сравним поведение всех методов:
Сравнительная таблица методов:
| Число | Math.floor() | Math.ceil() | Math.round() | Math.trunc() |
|---|---|---|---|---|
| 4.7 | 4 | 5 | 5 | 4 |
| 4.3 | 4 | 5 | 4 | 4 |
| -4.7 | -5 | -4 | -5 | -4 |
| -4.3 | -5 | -4 | -4 | -4 |
| -4.5 | -5 | -4 | -4 | -4 |
| 0.9 | 0 | 1 | 1 | 0 |
| -0.9 | -1 | 0 | -1 | 0 |
Из таблицы видно: Math.trunc() — единственный метод, который движется к нулю независимо от знака числа. Для положительных результат совпадает с Math.floor(), для отрицательных — с Math.ceil().
Когда использовать Math.trunc():
- Извлечение целой части числа без учёта округления — например, при разборе составных значений вроде версий программного обеспечения.
- Работа с целочисленными идентификаторами, полученными из дробных вычислений.
- Случаи, когда важна симметричность поведения для положительных и отрицательных чисел.
- Преобразование координат или размеров, где нужна только целая часть без математического округления.
Важно понимать: до появления Math.trunc() разработчики часто использовали побитовые операторы вроде ~~num или num | 0 для достижения того же эффекта. Однако Math.trunc() явно выражает намерение и работает корректнее с очень большими числами, не вызывая переполнения, характерного для 32-битных побитовых операций.
Таблица выбора метода округления:
| Задача | Рекомендуемый метод | Обоснование |
|---|---|---|
| Финансовые расчёты (цены, суммы) | Math.round() | Честное округление по математическим правилам |
| Отображение цен с копейками | toFixed(2) | Сохраняет незначащие нули для формата «19.00» |
| Деление на части (пагинация, блоки) | Math.ceil() | Гарантирует достаточное количество страниц/блоков |
| Вычисление поместившихся элементов | Math.floor() | Считает только полностью вмещающиеся единицы |
| Координаты и позиционирование | Math.round() | Предотвращает размытие на субпикселях |
| Размеры сетки (колонки, строки) | Math.floor() | Не допускает переполнения контейнера |
| Извлечение целой части без округления | Math.trunc() | Симметричное поведение для ± чисел |
| Вычисление индексов массивов | Math.floor() | Гарантирует валидные целочисленные индексы |
| Процент выполнения задачи | Math.ceil() | Избегает показа «100%» при 99.x% |
Как методы округления ведут себя с разными типами данных
Мы разобрали работу методов округления с числами, но что произойдёт, если передать им строку, массив или другой тип данных? JavaScript — язык с динамической типизацией, и его способность неявно преобразовывать типы может как помочь, так и создать трудноуловимые ошибки.
Все методы объекта Math перед выполнением операции пытаются преобразовать входящий аргумент в число. Этот процесс происходит автоматически через внутренний механизм Number(). Давайте посмотрим, как это работает на практике:
Строки с числовым содержимым успешно преобразуются:
Math.round("4.7"); // 5 -- строка преобразуется в число
Math.floor("8.2"); // 8
Math.ceil("-3.1"); // -3
Math.trunc("15.99"); // 15
Строки с нечисловым содержимым превращаются в NaN:
Math.round("hello"); // NaN
Math.floor("abc123"); // NaN
Math.ceil("12.5px"); // NaN -- даже если начинается с цифр
Пустые строки и пробелы преобразуются в ноль:
Math.round(""); // 0
Math.floor(" "); // 0
Массивы показывают неожиданное поведение:
Math.round([4.7]); // 5 -- массив с одним числом работает Math.floor([8, 2]); // NaN -- несколько элементов дают NaN Math.ceil([]); // 0 -- пустой массив преобразуется в 0
Специальные значения:
Math.round(null); // 0 -- null преобразуется в 0 Math.floor(undefined); // NaN -- undefined не может стать числом Math.ceil(true); // 1 -- булево true становится 1 Math.trunc(false); // 0 -- булево false становится 0
Объекты обычно превращаются в NaN, если у них нет специального метода преобразования:
Math.round({value: 5}); // NaN
Math.floor(new Date()); // число миллисекунд -- Date преобразуется в timestamp
Что происходит при получении NaN
Результат NaN (Not-a-Number) — это специальное числовое значение, которое означает невалидную математическую операцию. Все методы округления возвращают NaN, если не могут преобразовать аргумент в валидное число.
Коварство NaN в том, что он не равен самому себе: NaN === NaN возвращает false. Для проверки нужно использовать специальные функции:
const result = Math.round("текст");
Number.isNaN(result); // true -- современный способ
isNaN(result); // true -- старый способ, менее надёжный
Практические рекомендации: всегда валидируйте данные перед передачей в методы округления, особенно если они приходят от пользователя или из внешних источников. Явное преобразование через Number() с последующей проверкой помогает избежать неожиданных результатов в продакшене.
Как округлить число до нужного количества знаков после запятой
Все рассмотренные методы Math округляют только до целого числа. Но что делать, когда нужно оставить определённое количество знаков после запятой? Например, отобразить цену с двумя десятичными знаками или координату с точностью до трёх знаков. Для этого существует универсальный паттерн, основанный на математической манипуляции с разрядами.
Базовая формула округления до n знаков
Логика проста: нужно временно сдвинуть разряды влево (умножением), применить округление к целому числу, а затем вернуть разряды обратно (делением):
// Округление до n знаков после запятой Math.round(num * 10 ** n) / 10 ** n
Здесь 10 ** n — это возведение 10 в степень n. Для двух знаков это 100, для трёх — 1000 и так далее.
Практические примеры:
// Округление до 2 знаков Math.round(3.14159 * 100) / 100 // 3.14 Math.round(2.345 * 100) / 100 // 2.35 // Округление до 3 знаков Math.round(3.14159 * 1000) / 1000 // 3.142 // Округление до 1 знака Math.round(7.89 * 10) / 10 // 7.9
Формулы для других методов округления
Этот паттерн работает не только с Math.round(), но и с остальными методами:
Для округления вниз (floor) до n знаков:
Math.floor(num * 10 ** n) / 10 ** n // Примеры: Math.floor(3.14159 * 100) / 100 // 3.14 Math.floor(7.999 * 10) / 10 // 7.9
Для округления вверх (ceil) до n знаков:
Math.ceil(num * 10 ** n) / 10 ** n // Примеры: Math.ceil(3.141 * 100) / 100 // 3.15 Math.ceil(7.001 * 10) / 10 // 7.1
Для усечения (trunc) до n знаков:
Math.trunc(num * 10 ** n) / 10 ** n // Примеры: Math.trunc(3.999 * 100) / 100 // 3.99 Math.trunc(-3.999 * 100) / 100 // -3.99
Альтернатива через Math.pow()
В более старом коде вместо оператора возведения в степень ** можно встретить метод Math.pow():
Math.round(num * Math.pow(10, n)) / Math.pow(10, n)
Результат идентичен, но современный синтаксис 10 ** n более читаем и лаконичен.
Таблица результатов для разных значений n
| Исходное число | n=1 | n=2 | n=3 |
|---|---|---|---|
| 3.14159 | 3.1 | 3.14 | 3.142 |
| 7.8956 | 7.9 | 7.90 | 7.896 |
| 2.3333 | 2.3 | 2.33 | 2.333 |
| 15.6789 | 15.7 | 15.68 | 15.679 |
| 0.12345 | 0.1 | 0.12 | 0.123 |
Важное замечание: этот метод не гарантирует сохранение незначащих нулей. Например, Math.round(2.1 * 100) / 100 вернёт 2.1, а не 2.10. Для форматирования с фиксированным количеством цифр используется другой подход, который мы рассмотрим далее.
Округление через toFixed(): когда использовать и какие есть подводные камни
Существует ещё один способ округления до заданного количества знаков после запятой — метод toFixed(). В отличие от манипуляций с Math, этот метод вызывается непосредственно на числе и выглядит гораздо проще:
const num = 3.14159; num.toFixed(2); // "3.14"
На первый взгляд, toFixed() кажется идеальным решением: лаконичный синтаксис, понятная логика, встроенное форматирование. Однако у этого метода есть критически важная особенность, которую нельзя игнорировать.
Главный подводный камень: toFixed() возвращает строку.
Это не число типа Number, а именно строка типа String. Для отображения в интерфейсе это идеально — мы получаем красиво отформатированное значение с нужным количеством знаков, включая незначащие нули:
const price = 19.5; price.toFixed(2); // "19.50" -- строка с двумя знаками
Проблемы начинаются, когда результат нужно использовать в дальнейших вычислениях. Математические операции со строками дают неожиданные результаты или ошибки:
const result = (10.567).toFixed(2); // "10.57" -- строка result + 5; // "10.575" -- конкатенация строк, не сложение! result * 2; // 21.14 -- работает из-за неявного преобразования
Решение: если после toFixed() нужны вычисления, результат следует преобразовать обратно в число через parseFloat() или унарный плюс:
const num = 3.14159; const rounded = parseFloat(num.toFixed(2)); // 3.14 -- число // Или короче: const rounded2 = +num.toFixed(2); // 3.14 -- число
Плюсы toFixed():
- Сохраняет незначащие нули — (2.1).toFixed(2) даст «2.10», что важно для отображения цен и процентов.
- Простой и читаемый синтаксис, не требующий математических манипуляций.
- Идеален для финального форматирования перед выводом пользователю.
Минусы toFixed():
- Возвращает строку, что создаёт проблемы при продолжении вычислений.
- Может привести к трудноуловимым багам, если забыть о типе результата.
- Округление происходит по правилам Math.round() — нет возможности выбрать floor или ceil.
- Иногда показывает странное поведение из-за проблем точности с плавающей точкой: (1.005).toFixed(2) может вернуть «1.00» вместо ожидаемого «1.01».
Рекомендация: используйте toFixed() для финального форматирования данных перед отображением, но избегайте его в середине вычислительных цепочек. Для промежуточных расчётов надёжнее применять формулы с Math.round() и его аналогами.
Практические примеры использования округления
Теория становится понятнее, когда мы видим её применение в реальных задачах. Давайте рассмотрим типовые сценарии из веб-разработки, где методы округления играют ключевую роль.
Финансовые расчёты
Представим интернет-магазин, где нужно рассчитать итоговую сумму заказа со скидкой и округлить до копеек:
const items = [
{ name: "Книга", price: 299.99 },
{ name: "Ручка", price: 15.50 },
{ name: "Блокнот", price: 89.90 }
];
// Считаем общую сумму
let total = items.reduce((sum, item) => sum + item.price, 0);
// total = 405.39
// Применяем скидку 15%
const discount = 0.15;
let discountedTotal = total * (1 - discount);
// discountedTotal = 344.5815 -- возникла дробная копейка
// Округляем до двух знаков (копеек)
const finalTotal = Math.round(discountedTotal * 100) / 100;
// finalTotal = 344.58
console.log(`Итоговая сумма к оплате: ${finalTotal} руб.`);
// Результат: "Итоговая сумма к оплате: 344.58 руб."
В финансовых операциях критически важно использовать именно Math.round() для корректного округления до ближайшей копейки. Использование Math.floor() всегда округлит в пользу магазина, а Math.ceil() — в пользу покупателя, что может привести к проблемам.

В финансовых расчетах критически важна точность. Иллюстрация показывает, как математическое округление с помощью Math.round() позволяет получить корректную итоговую сумму после применения скидки.
UI и frontend: разметка, размеры, шрифты
Верстальщики постоянно сталкиваются с необходимостью округления при динамических расчётах размеров. Рассмотрим задачу создания сетки с тремя колонками:
const containerWidth = 799.8; // Ширина контейнера в пикселях
const columnCount = 3; // Количество колонок
// Вычисляем ширину одной колонки
const columnWidth = Math.floor(containerWidth / columnCount);
// columnWidth = 266
console.log(`Ширина одной колонки: ${columnWidth}px`);
Здесь мы используем Math.floor(), чтобы гарантировать: все три колонки точно поместятся в контейнер. Если бы применили Math.ceil(), получилось бы 267px, и три колонки заняли бы 801px — больше доступного пространства.
Центрирование элемента по горизонтали:
const parentWidth = 800; // Ширина родительского блока const childWidth = 375; // Ширина вложенного элемента // Находим левый отступ для центрирования const leftOffset = Math.round((parentWidth - childWidth) / 2); // leftOffset = 213 element.style.left = leftOffset + "px";
Использование Math.round() здесь предотвращает размытие элемента и смещение на доли пикселя, которые браузер может отрисовать некорректно.
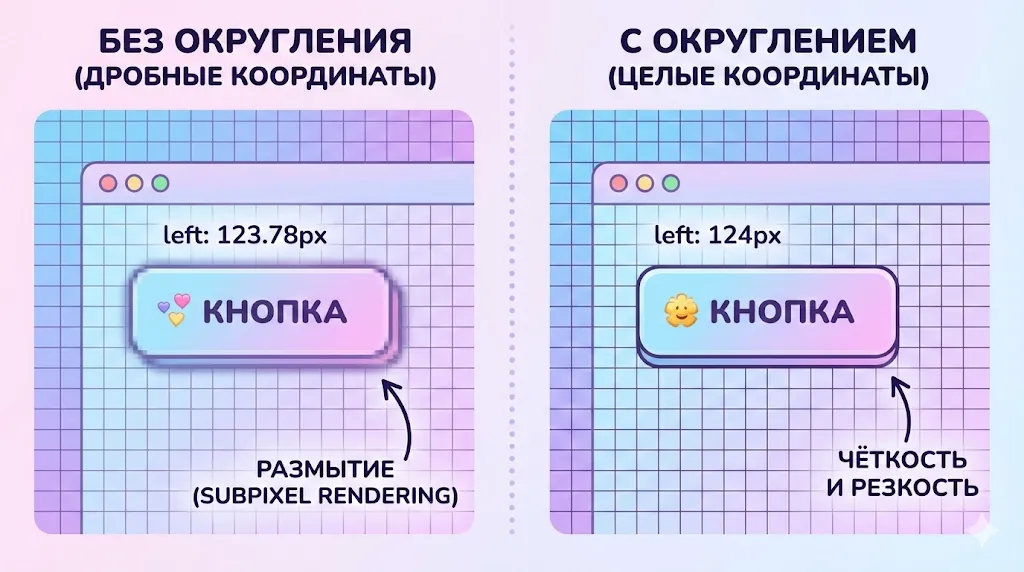
Эта иллюстрация демонстрирует, почему важно округлять координаты при работе с CSS. Дробные значения могут привести к размытию элемента, в то время как целые пиксели обеспечивают четкую и резкую отрисовку.
Работа с координатами
При создании интерактивных элементов — перетаскиваемых объектов, анимаций, canvas-графики — координаты часто получаются дробными, но CSS требует целых значений:
let x = 123.78; // Текущая позиция из расчётов // Округляем координату до целого пикселя element.style.left = Math.round(x) + "px"; // "124px"
Без округления браузер может применить субпиксельное позиционирование, что приведёт к размытости элемента или дрожанию при анимации.
Вычисление угла поворота:
const angleInRadians = 1.5708; // Радианы
const angleInDegrees = angleInRadians * (180 / Math.PI);
// angleInDegrees = 90.00021045914971
const roundedAngle = Math.round(angleInDegrees);
// roundedAngle = 90
element.style.transform = `rotate(${roundedAngle}deg)`;
Эти примеры показывают, что выбор метода округления зависит от контекста: в финансах важна честность, в вёрстке — предотвращение переполнения, в координатах — чёткость отображения.
Типичные ошибки при округлении в JavaScript и как их избежать
Даже опытные разработчики допускают ошибки при работе с округлением. Давайте рассмотрим самые распространённые из них и научимся их предотвращать.
Попытка передать второй аргумент в Math.round()
Многие новички интуитивно пытаются написать Math.round(1.2345, 2), ожидая получить округление до двух знаков. Однако метод игнорирует второй параметр и возвращает целое число:
Math.round(1.2345, 2); // 1 -- второй аргумент проигнорирован
Правильное решение — использовать формулу с умножением и делением: Math.round(1.2345 * 100) / 100.
Ожидание точности при работе с дробями
Разработчики забывают о проблемах плавающей точки и удивляются неожиданным результатам:
Math.round(0.1 + 0.2); // 0 -- потому что 0.1 + 0.2 = 0.30000000000000004
Решение: сначала корректировать точность, потом округлять — Math.round((0.1 + 0.2) * 10) / 10 даст корректный результат 0.3.
Путаница с поведением отрицательных чисел
Особенно часто возникает с Math.floor() и Math.ceil():
Math.floor(-4.7); // -5, а не -4 как ожидают некоторые Math.ceil(-4.7); // -4, а не -5
Если нужно просто отбросить дробную часть без учёта знака, используйте Math.trunc().
Забывание о типе результата toFixed()
Классическая ловушка — использовать результат toFixed() в вычислениях, забывая о преобразовании типа:
const price = (19.99).toFixed(2); // "19.99" -- строка! const total = price + 5; // "19.995" -- конкатенация строк
Всегда оборачивайте в parseFloat() или применяйте унарный плюс: +price.toFixed(2).
Округление перед вычислениями вместо округления результата
Преждевременное округление накапливает ошибки:
// Неправильно: const a = Math.round(3.7 * 100) / 100; // 4 const b = Math.round(2.3 * 100) / 100; // 2 const sum = a + b; // 6 -- потеряли точность // Правильно: const sum = Math.round((3.7 + 2.3) * 100) / 100; // 6
Золотое правило: выполняйте все вычисления с полной точностью и округляйте только финальный результат.
Игнорирование валидации входящих данных
Передача нечисловых значений в методы округления без проверки:
const userInput = "abc"; const result = Math.round(userInput); // NaN -- и приложение сломано
Всегда проверяйте данные перед округлением: if (typeof value === ‘number’ && !isNaN(value)).
Использование побитовых операторов для округления больших чисел
Старый трюк ~~num или num | 0 работает как усечение, но ломается на числах больше 2³¹:
~~2147483648; // -2147483648 -- переполнение! Math.trunc(2147483648); // 2147483648 -- корректно
Для надёжности всегда используйте методы Math, а не побитовые хаки.
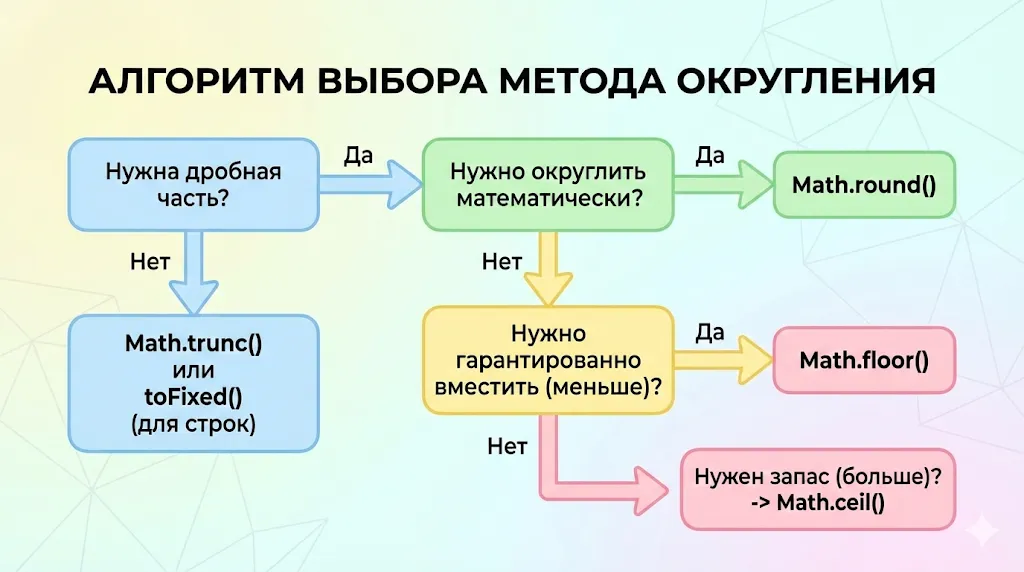
Сохраните эту схему как шпаргалку. Она поможет вам быстро определить, какой метод округления лучше всего подходит для вашей конкретной задачи, будь то финансовые расчеты, верстка или работа с данными.
Заключение
Мы разобрали все основные методы округления в JavaScript, их особенности и подводные камни. Теперь давайте систематизируем эти знания в виде практического руководства по выбору подходящего инструмента.
- Округление в JavaScript — это не простая операция, а важный инструмент для корректной работы с числами. Неправильный выбор метода может привести к ошибкам в расчетах и отображении данных.
- Объект Math предоставляет несколько методов округления, каждый из которых решает свою задачу. Math.round, Math.floor, Math.ceil и Math.trunc по-разному ведут себя, особенно при работе с отрицательными числами.
- Проблемы точности чисел связаны с форматом хранения Number и стандартом IEEE 754. Их необходимо учитывать при любых вычислениях с дробями.
- Для округления до нужного количества знаков используется математический сдвиг разрядов. Этот подход универсален и применим ко всем методам Math.
- Метод toFixed удобен для форматирования, но возвращает строку. Его следует использовать только для вывода данных, а не для дальнейших расчетов.
- Корректное округление особенно важно в финансовых операциях, верстке интерфейсов и работе с координатами. Округлять следует только финальный результат вычислений.
Если вы только начинаете осваивать профессию frontend-разработчика и хотите глубже разобраться в работе с числами, рекомендуем обратить внимание на подборку курсов по JavaScript. В программах обучения есть как теоретическая часть, так и практические задания для закрепления навыков округления и вычислений.
Рекомендуем посмотреть курсы по JavaScript разработке
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Fullstack-разработчик на JavaScript
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
147 000 ₽
|
От
12 250 ₽/мес
0% на 24 месяца
|
Длительность
9 месяцев
|
Старт
в любое время
|
Подробнее |
|
Автоматизированное тестирование веб-приложений на JavaScript
|
Skillbox
218 отзывов
|
Цена
Ещё -47% по промокоду
48 408 ₽
64 548 ₽
|
От
4 034 ₽/мес
Без переплат на 1 год.
5 379 ₽/мес
|
Длительность
4 месяца
|
Старт
30 января
|
Подробнее |
|
Полный курс по JavaScript — С нуля до результата!
|
Stepik
33 отзыва
|
Цена
2 990 ₽
|
От
748 ₽/мес
|
Длительность
1 неделя
|
Старт
в любое время
|
Подробнее |
|
Backend-разработка на Node.js
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
28 500 ₽
50 000 ₽
|
От
2 500 ₽/мес
Без переплат на 1 год.
|
Длительность
6 месяцев
|
Старт
в любое время
|
Подробнее |
|
Профессия Fullstack-разработчик на Python
|
Skillbox
218 отзывов
|
Цена
Ещё -20% по промокоду
146 073 ₽
292 147 ₽
|
От
4 296 ₽/мес
|
Длительность
12 месяцев
|
Старт
30 января
|
Подробнее |

Agile-тестирование: методологии, принципы и преимущества
Agile-тестирование — это непрерывный процесс обеспечения качества, интегрированный в каждую стадию разработки. Мы рассмотрим ключевые принципы, популярные методологии (Scrum, Kanban, XP) и подходы, такие как TDD, BDD и автоматизация. Узнайте, как стать эффективным тестировщиком в Agile-команде.

Как составить бриф, который поможет графическому дизайнеру
Хотите избежать бесконечных правок и задержек? Разбираем, как грамотно составить бриф для дизайнера, чтобы получить точный и качественный результат.

Желтый цвет в дизайне: вдохновение или вызов?
Желтый может как привлечь внимание, так и перегрузить восприятие. Разбираемся, как правильно интегрировать его в графический дизайн!

Kotlin и Java: сравнение языков для разработчиков
Что выбрать: Kotlin или Java? Разбираем ключевые особенности, синтаксис и производительность языков, чтобы помочь вам сделать оптимальный выбор