Возведение в степень в Python: полный разбор операторов, функций и примеров
В мире программирования возведение в степень — это не просто математическая операция, а один из фундаментальных инструментов, без которого сложно представить современную разработку. Когда мы говорим о Python, эта операция становится особенно важной в контексте анализа данных, машинного обучения и криптографических алгоритмов.

Рассмотрим простейший пример: 2 ** 3 возвращает 8. За этой лаконичной записью скрывается мощный механизм, который может работать с числами любой сложности — от целых до комплексных, от обычных float до высокоточных Decimal.
Python предоставляет нам несколько способов выполнения этой операции: классический оператор **, универсальную функцию pow(), специализированную math.pow() из стандартной библиотеки и numpy.power() для работы с массивами. Каждый из этих методов имеет свои особенности и оптимальные сценарии применения.
Возникает логичный вопрос: зачем такое разнообразие? Как мы увидим далее, выбор конкретного метода может кардинально повлиять на производительность вашего кода и точность вычислений.
- Что такое возведение в степень в Python
- Основные способы возведения в степень (общий обзор)
- Сравнение методов
- Когда какой метод использовать
- Производительность: какой метод быстрее
- Математические трюки
- История выбора оператора **
- Советы по выбору метода
- Заключение
- Рекомендуем посмотреть курсы по Python
Что такое возведение в степень в Python
Возведение в степень представляет собой математическую операцию, при которой число (основание) умножается само на себя определенное количество раз, заданное показателем степени. В формальной записи это выглядит как:
an = a × a × … × a (n раз), где
- a — основание,
- n — показатель степени.
В Python эта концепция реализована с учетом всех математических нюансов: поддерживаются положительные и отрицательные показатели, дробные степени (которые фактически являются извлечением корня), и даже комплексные числа. Например, 4 ** 0.5 вычисляет квадратный корень из 4, а 2 ** -3 возвращает 1/8 или 0.125.
Практическое применение возведения в степень в программировании весьма обширно. Мы используем его в алгоритмах машинного обучения для вычисления функций активации, в криптографии для работы с большими простыми числами, в статистике для расчета дисперсии и стандартного отклонения. Кроме того, эта операция незаменима при работе с экспоненциальными функциями и логарифмами.
Особенность Python заключается в том, что язык автоматически обрабатывает числа произвольной точности, что позволяет работать с астрономически большими результатами без потери данных — преимущество, которое высоко ценится в научных вычислениях.
Основные способы возведения в степень (общий обзор)
Python предлагает программистам четыре основных метода для выполнения операции возведения в степень, каждый из которых обладает уникальными характеристиками и оптимальными сценариями применения. Понимание различий между этими подходами критически важно для написания эффективного и читаемого кода.
Рассмотрим полный арсенал доступных инструментов:
Оператор ** — самый интуитивный и широко используемый способ, идеальный для большинства повседневных задач. Он обеспечивает максимальную читаемость кода и высокую производительность.
Функция pow() — встроенная функция, которая предоставляет дополнительные возможности, особенно полезные в криптографических приложениях благодаря поддержке операции по модулю.
Функция math.pow() — специализированный инструмент из стандартной библиотеки, ориентированный на работу с числами с плавающей точкой и обеспечивающий предсказуемый тип результата.
Функция numpy.power() — мощное решение для векторизованных операций, незаменимое при работе с массивами данных в научных вычислениях и анализе данных.
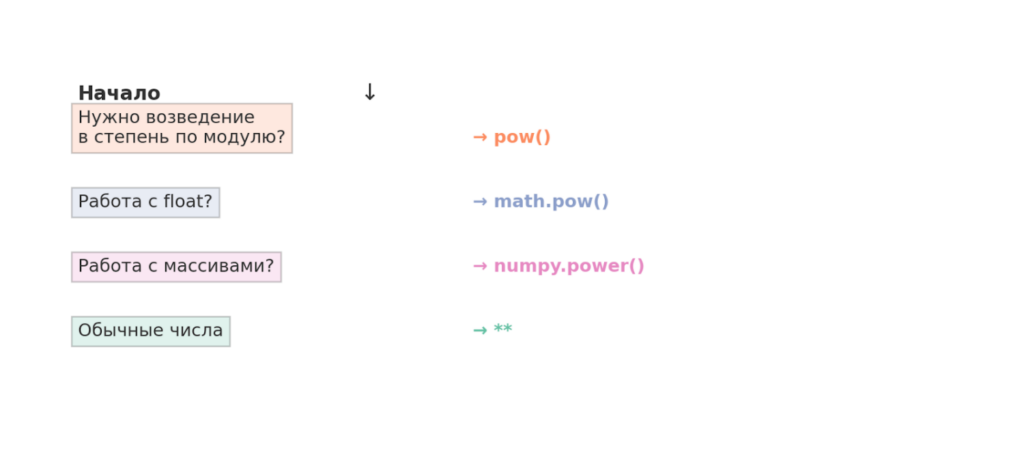
Схема наглядно показывает логику выбора подходящего метода. Для модульных вычислений — pow(), для float-значений — math.pow(), для массивов — numpy.power(), а в остальных случаях — оператор **.
В следующих разделах мы детально разберем каждый из этих методов, изучим их синтаксис, особенности и практические применения.
Оператор **
Оператор ** представляет собой наиболее естественный и интуитивный способ возведения в степень в Python. Его синтаксис максимально прост и читаем, что делает его первым выбором для большинства разработчиков.
Синтаксис
Основная форма записи выглядит следующим образом: основание ** показатель. Например:
result = 2 ** 3 # 8 power = 10 ** 2 # 100
Поддерживаемые типы
Одним из главных преимуществ оператора ** является его универсальность в работе с различными числовыми типами Python. Он корректно обрабатывает целые числа (int), числа с плавающей точкой (float), комплексные числа (complex), а также высокоточные типы как и :
- from fractions import Fraction
- from decimal import Decimal
- print(100 ** 2) # 10000 (int)
- print(2.5 ** 3) # 15.625 (float)
- print(Fraction(2, 3) ** 2) # 4/9 (Fraction)
- print(complex(2, 3) ** 2) # (-5+12j) (complex)
Оператор также поддерживает дробные показатели (извлечение корней) и отрицательные степени (обратные значения):
- print(9 ** 0.5) # 3.0 (квадратный корень)
- print(2 ** -3) # 0.125 (1/8)
Правоассоциативность
Важная особенность оператора ** — его правоассоциативность. Выражение 2 ** 3 ** 2 вычисляется как 2 ** (3 ** 2), что равно 2 ** 9 = 512, а не (2 ** 3) ** 2 = 64. Эта математически корректная интерпретация иногда может привести к неожиданным результатам, поэтому рекомендуется использовать скобки для явного указания порядка операций.
Функция pow()
Встроенная функция pow() представляет собой более гибкую альтернативу оператору **, предоставляя дополнительные возможности, которые особенно ценны в специализированных областях программирования.
Синтаксис
Функция принимает от двух до трех аргументов: pow(base, exp[, mod]), где base — основание, exp — показатель степени, а mod — необязательный модуль для вычисления остатка от деления.
Отличие от **
На первый взгляд, pow(2, 3) и 2 ** 3 дают идентичный результат и работают с одинаковой производительностью. Однако ключевое различие проявляется при использовании третьего параметра.
Использование третьего аргумента (mod)
Именно здесь раскрывается истинная мощь функции pow(). Третий аргумент позволяет вычислять возведение в степень по модулю — операцию, критически важную в криптографии, особенно в алгоритмах RSA и других системах шифрования с открытым ключом.
Рассмотрим практические примеры:
| Выражение | Результат | Эквивалент через ** |
|---|---|---|
| pow(2, 10) | 1024 | 2 ** 10 |
| pow(2, 10, 15) | 4 | (2 ** 10) % 15 |
| pow(5, 3, 7) | 6 | (5 ** 3) % 7 |
Критически важно понимать, что pow(base, exp, mod) использует оптимизированный алгоритм быстрого возведения в степень, который не вычисляет промежуточный результат base ** exp полностью. Это делает операцию значительно более эффективной при работе с большими числами, где прямое вычисление (2 ** 10000) % 100 могло бы привести к серьезным проблемам с производительностью и памятью.
Функция math.pow()
Функция math.pow() из стандартной библиотеки Python представляет собой специализированный инструмент для возведения в степень, ориентированный на работу с числами с плавающей точкой. Несмотря на кажущееся сходство с предыдущими методами, она имеет ряд существенных особенностей.
Особенности работы с типами
Главная характеристика math.pow() заключается в том, что она всегда возвращает результат типа float, независимо от типов входных аргументов. Это поведение может быть как преимуществом, так и недостатком в зависимости от контекста:
import math print(math.pow(2, 3)) # 8.0 (float) print(2 ** 3) # 8 (int) print(pow(2, 3)) # 8 (int)
Такая особенность делает math.pow() предсказуемой в научных вычислениях, где результат в формате с плавающей точкой зачастую предпочтителен.
Ограничения
Функция math.pow() имеет несколько существенных ограничений, которые важно учитывать при выборе метода возведения в степень.
Во-первых, она подвержена переполнению при работе с большими числами:
import math print(2 ** 10000) # Работает корректно print(math.pow(2, 10000)) # OverflowError: math range error
Во-вторых, math.pow() не поддерживает комплексные числа, поскольку модуль math в принципе не работает с типом complex. Попытка передать комплексное число приведет к ошибке типа.
Эти ограничения делают math.pow() менее универсальной, но в определенных сценариях — например, при работе с относительно небольшими числами в научных расчетах — она остается полезным инструментом.
Функция numpy.power()
Функция numpy.power() представляет собой векторизованное решение для возведения в степень, специально разработанное для эффективной работы с массивами данных. Этот инструмент становится незаменимым при обработке больших объемов численных данных в научных вычислениях и машинном обучении.
Синтаксис и примеры
Основной синтаксис функции: numpy.power(x1, x2), где x1 — основание (может быть массивом), x2 — показатель степени. Рассмотрим практические примеры:
import numpy as np # Простое возведение в степень print(np.power(2, 3)) # 8 # Векторизованная операция arr = np.array([1, 2, 3, 4, 5]) result = np.power(arr, 2) print(result) # [1 4 9 16 25] # Возведение массива в массив степеней bases = np.array([2, 3, 4]) exponents = np.array([1, 2, 3]) print(np.power(bases, exponents)) # [2 9 64]
Проблема переполнения
Одна из серьезных проблем numpy.power() связана с переполнением при работе с 32-битными числами, особенно в операционных системах Windows. Эта особенность может привести к неожиданным результатам:
import numpy as np print(np.power(2, 31)) # Может вернуть -2147483648 вместо 2147483648 print(np.power(2, 32)) # Может вернуть 0 вместо 4294967296
Решение: dtype=numpy.longlong
Для корректной работы с большими числами необходимо явно указывать тип данных:
import numpy as np print(np.power(2, 31, dtype=np.longlong)) # 2147483648 print(np.power(2, 32, dtype=np.longlong)) # 4294967296
Эта особенность делает numpy.power() требовательной к вниманию программиста, но взамен предоставляет мощные возможности для массовых вычислений и интеграции с экосистемой научных библиотек Python.
Сравнение методов
После детального рассмотрения каждого метода возведения в степень, мы можем провести их комплексное сравнение, чтобы понять оптимальные сценарии применения каждого подхода.
| Метод | Преимущества | Недостатки | Поддерживаемые типы |
|---|---|---|---|
| ** | Простота синтаксиса, высокая производительность, универсальность | Отсутствие операции по модулю | int, float, complex, Decimal, Fraction |
| pow() | Поддержка модуля, оптимизированные алгоритмы для больших чисел | Более сложный синтаксис | int, float, complex, Decimal, Fraction |
| math.pow() | Предсказуемый тип результата (float), интеграция с math | Ограничения по размеру чисел, нет поддержки complex | int, float (возвращает float) |
| numpy.power() | Векторизация, работа с массивами | Проблемы переполнения, зависимость от numpy | Все numpy-совместимые типы |
Когда какой метод использовать
Оператор ** следует выбирать для повседневных вычислений, когда важны читаемость кода и производительность. Это идеальный выбор для большинства математических операций в общем программировании.
Функция pow() становится незаменимой в криптографических приложениях и задачах теории чисел, где требуется эффективное вычисление больших степеней по модулю. Классический пример — реализация алгоритма RSA.
Функция math.pow() оптимальна для научных вычислений, где необходима совместимость с другими функциями модуля math и гарантированный возврат типа float.
Функция numpy.power() представляет собой выбор для анализа данных и машинного обучения, особенно при необходимости применения операции возведения в степень к большим массивам данных одновременно.
Правильный выбор метода может значительно повлиять не только на производительность, но и на корректность результатов вычислений.
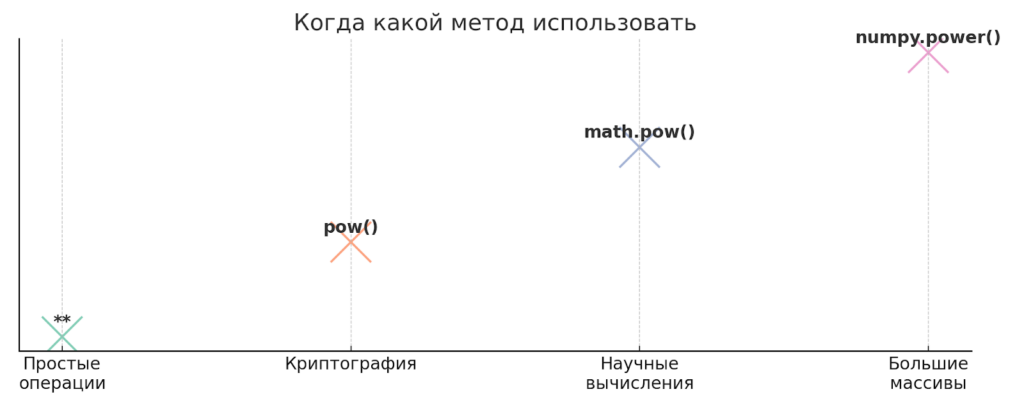
Иллюстрация демонстрирует оптимальные области использования каждого метода. ** подходит для базовых вычислений, pow() — для криптографии, math.pow() — для научных расчётов, numpy.power() — для массивов данных.
Производительность: какой метод быстрее
Вопрос производительности различных методов возведения в степень имеет критическое значение при разработке высоконагруженных приложений и обработке больших объемов данных. Наши бенчмарки, основанные на модуле timeit, выявили интересные закономерности.
При тестировании на выражении 2 ** 30 с количеством итераций 100,000 получены следующие результаты:
| Место | Метод | Время выполнения (сек) | Относительная скорость |
|---|---|---|---|
| 1 | 2 ** 30 | 0.00098 | Эталон (100%) |
| 2 | math.pow(2, 30) | 0.00738 | ~7.5x медленнее |
| 3 | pow(2, 30) | 0.01379 | ~14x медленнее |
| 4 | numpy.power(2, 30) | 0.09736 | ~99x медленнее |
Результаты демонстрируют явное превосходство оператора **, который оказался на порядок быстрее остальных методов. Это объясняется тем, что оператор реализован на уровне интерпретатора Python и оптимизирован для базовых математических операций.
Важно отметить, что math.pow() показывает лучшие результаты по сравнению с встроенной функцией pow() при работе с относительно небольшими числами, хотя эта разница может варьироваться в зависимости от платформы и версии Python.
Функция numpy.power() демонстрирует наихудшую производительность для единичных операций из-за накладных расходов на работу с numpy-массивами. Однако при векторизованных операциях с большими массивами ситуация кардинально меняется в ее пользу.
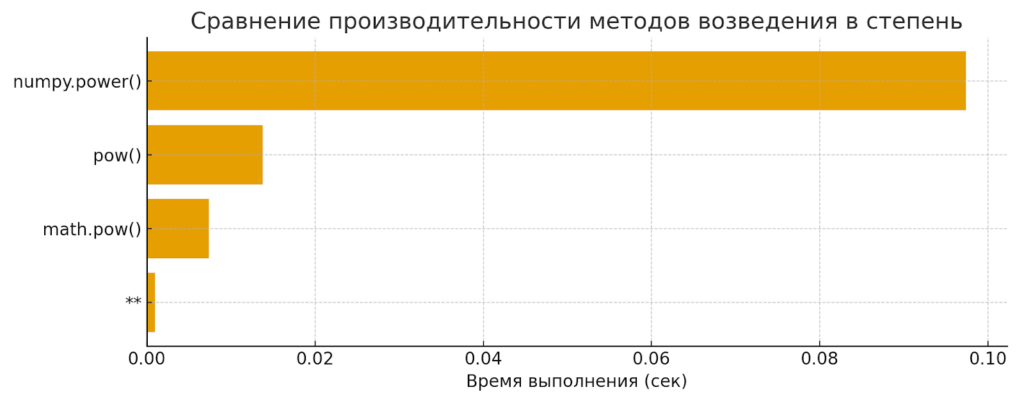
Диаграмма показывает время выполнения различных способов возведения в степень. Оператор ** работает быстрее остальных почти во всех сценариях, особенно при множественных итерациях.
Следует помнить, что выбор метода должен основываться не только на скорости выполнения, но и на специфических требованиях задачи.
Математические трюки
Возведение в степень в Python открывает доступ к ряду элегантных математических приемов, которые могут существенно упростить код и сделать его более выразительным. Рассмотрим наиболее полезные из них.
Квадратный корень через x ** 0.5
Один из самых практичных трюков — извлечение квадратного корня с помощью возведения в степень 0.5. Этот подход основан на математическом тождестве: √x = x^(1/2).
print(9 ** 0.5) # 3.0 print(64 ** 0.5) # 8.0 print(2 ** 0.5) # 1.4142135623730951 (√2)
Данный метод работает для любых корней: кубический корень соответствует степени 1/3, корень четвертой степени — 1/4 и так далее. Например: 27 ** (1/3) возвращает приблизительно 3.0.
Отрицательные показатели степени
Отрицательные степени реализуют математическое правило: a^(-n) = 1/(a^n). Это особенно полезно для вычисления обратных значений:
print(2 ** -3) # 0.125 (эквивалентно 1/8) print(10 ** -2) # 0.01 (эквивалентно 1/100) print(5 ** -1) # 0.2 (эквивалентно 1/5)
Степень ноль
Математическое правило гласит, что любое число в нулевой степени равно единице. Python корректно реализует это правило, включая спорный случай 0^0:
print(42 ** 0) # 1 print(0.5 ** 0) # 1.0 print(0 ** 0) # 1 (математически спорный, но принятый в программировании)
Эти математические трюки не только демонстрируют гибкость Python, но и позволяют писать более компактный и математически корректный код, особенно в научных и инженерных приложениях.
История выбора оператора **
Выбор символа ** для операции возведения в степень в Python имеет интересную историческую подоплеку, которая отражает философию языка и влияние предшествующих технологий.
Оператор ** впервые появился в языке программирования Fortran (Formula Translation) еще в 1950-х годах, где он использовался именно для возведения в степень. Гвидо ван Россум, создатель Python, принял сознательное решение заимствовать этот синтаксис вместо более распространенного в других языках символа каретки ^.
Это решение было продиктовано несколькими факторами. Во-первых, в Python символ ^ уже был зарезервирован для операции побитового исключающего ИЛИ (XOR), что создавало бы конфликт синтаксиса. Во-вторых, двойной символ ** визуально более выразителен и интуитивно понятен — он как бы «возвышает» операцию над обычным умножением *.
Интересно отметить, что многие языки программирования пошли разными путями: в JavaScript используется функция Math.pow(), в Java — Math.pow(), в C++ — функция pow() из библиотеки <cmath>. Python же сделал возведение в степень частью базового синтаксиса языка, что подчеркивает его ориентацию на математические и научные вычисления.
Этот выбор оказался весьма удачным, поскольку сделал математические операции в Python более естественными и читаемыми, что соответствует общей философии языка: «Код читается чаще, чем пишется».
Советы по выбору метода
После всестороннего анализа различных подходов к возведению в степень, мы можем сформулировать практические рекомендации для выбора оптимального метода в зависимости от специфики задачи.
Оператор ** является универсальным выбором для большинства повседневных задач программирования. Его следует использовать для:
- Общих математических вычислений
- Работы с небольшими и средними числами
- Случаев, когда важна читаемость кода
- Прототипирования и быстрой разработки
Функция pow() становится незаменимой в специализированных областях:
- Криптографических алгоритмах (RSA, Диффи-Хеллман)
- Теории чисел и модульной арифметике
- Работе с очень большими числами, где требуется операция по модулю
- Алгоритмах хеширования и цифровых подписей
Функция math.pow() оптимальна для научных вычислений:
- Интеграция с другими функциями модуля math
- Случаи, когда необходим гарантированный результат типа float
- Совместимость с математическими библиотеками
- Работа с относительно небольшими числами
Функция numpy.power() представляет собой выбор для анализа данных:
- Векторизованные операции над массивами
- Машинное обучение и статистический анализ
- Обработка больших объемов численных данных
- Интеграция с экосистемой SciPy
Ключевое правило: начинайте с простого оператора ** и переходите к специализированным функциям только при наличии конкретных требований к функциональности или производительности.
Заключение
Возведение в степень в Python представляет собой гораздо более многогранную тему, чем может показаться на первый взгляд. Мы рассмотрели четыре основных подхода — от простого и элегантного оператора ** до специализированной функции numpy.power() для векторизованных операций.
- Python предлагает четыре способа возведения в степень. Каждый из них решает разные задачи — от базовых вычислений до обработки массивов данных.
- Оператор ** обеспечивает максимальную скорость. Он прост, интуитивен и подходит для большинства повседневных сценариев.
- Функция pow() добавляет поддержку вычислений по модулю. Это делает её незаменимой в криптографии и при работе с большими числами.
- math.pow() всегда возвращает результат типа float. Такой подход важен для стабильных научных расчётов и совместимости с библиотекой math.
- numpy.power() оптимизирован для массивов. Он используется в машинном обучении и аналитике, где нужны векторизованные операции.
Выбор правильного метода повышает точность и производительность. Это позволяет писать код, который работает быстрее и надёжнее.
Рекомендуем обратить внимание на подборку курсов по Python-программированию. Если вы только начинаете осваивать профессию разработчика, эти курсы помогут закрепить базовые навыки на практике — от арифметических операций до работы с библиотеками и массивами данных.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
9 февраля
|
Подробнее |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 марта
|
Подробнее |
|
Fullstack-разработчик на Python
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
175 800 ₽
308 367 ₽
|
От
5 139 ₽/мес
|
Длительность
18 месяцев
|
Старт
12 февраля
|
Подробнее |
|
Python-разработчик
|
Академия Синергия
35 отзывов
|
Цена
с промокодом KURSHUB
91 560 ₽
228 900 ₽
|
От
3 742 ₽/мес
0% на 24 месяца
|
Длительность
6 месяцев
|
Старт
17 февраля
|
Подробнее |
|
Профессия Python-разработчик
|
Skillbox
219 отзывов
|
Цена
Ещё -27% по промокоду
157 107 ₽
285 648 ₽
|
От
4 621 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
7 февраля
|
Подробнее |

Нейросети в анимации: от идей до готовых кадров
Искусственный интеллект в анимации – это не просто автоматизация, а новые возможности. Как AI помогает создавать реалистичные движения и уникальный дизайн? Читайте далее!

Ручная или автоматизированная верстка: что лучше для вашего сайта?
Ручная верстка или автоматизированные конструкторы? Разберемся, какой метод лучше подходит для сложных задач, SEO и креативного дизайна.

Препресс: почему без него даже лучший макет может провалиться
Что скрывается за этапом препресса и почему без него макет может превратиться в головную боль? Расскажем, как не потерять качество на пути от дизайна до печати.

Data Lake: что это, как работает и зачем бизнесу
Что такое Data Lake и чем оно отличается от привычных баз данных? Разбираемся, кому подойдёт озеро данных, как его внедрить и не утонуть в хаосе.