Булевы функции: что это такое, зачем нужны и как составлять таблицы истинности
В эпоху цифровых технологий и искусственного интеллекта понимание основ математической логики становится не просто полезным навыком, а необходимостью. Булевы функции — это фундаментальный инструмент, который лежит в основе работы всех современных вычислительных систем, от простейших логических схем до сложнейших нейронных сетей.

В этом курсе мы разберем, что представляют собой булевы функции, где они применяются и как правильно работать с таблицами истинности.
- Что это такое
- Где применяются
- Основные логические операции
- Таблица истинности: как она работает и как её построить
- Пример составления таблицы истинности
- Суперпозиция булевых функций
- Двойственные булевы функции
- Методы минимизации булевых выражений
- FAQ — Часто задаваемые вопросы
- Заключение
- Рекомендуем посмотреть курсы по Python
Что это такое
Булевы функции — это математический аппарат для описания логических операций, названный в честь британского математика Джорджа Буля, который в середине XIX века заложил основы математической логики. В отличие от привычных нам арифметических операций, работающих с действительными числами, булева алгебра оперирует исключительно значениями истинности: true (истина) и false (ложь), которые в цифровых системах представлены как 1 и 0 соответственно.
Можно сказать, что это своеобразный язык, на котором «говорят» все цифровые устройства. Каждая такая функция принимает на вход одно или несколько логических значений (операндов) и выдает единственный логический результат согласно определенному правилу.
Основные свойства:
- Работают только с двумя значениями: 0 (false) и 1 (true).
- Имеют четко определенные правила преобразования входных данных в выходные.
- Могут объединяться в сложные логические выражения.
- Лежат в основе всех цифровых вычислений и логических схем.
- Позволяют формализовать и автоматизировать процессы принятия решений.
Где применяются
Булевы функции находят широкое применение в различных областях современных технологий, от базовых логических схем до сложнейших систем искусственного интеллекта. Давайте рассмотрим основные сферы их использования.
В логических схемах и цифровой электронике они являются основой для построения всех вычислительных устройств. Каждый транзистор в процессоре, каждый логический элемент в микросхеме работает согласно принципам булевой алгебры. Например, простейший логический элемент «И» (AND) пропускает сигнал на выход только тогда, когда на оба его входа подается высокий уровень напряжения — именно так она реализуется конъюнкции на аппаратном уровне.
В программировании они используются для создания условных конструкций, циклов и алгоритмов принятия решений. Современные языки программирования активно используют логические операторы: в Python это and, or, not, в JavaScript — &&, ||, !. Рассмотрим практический пример: система аутентификации проверяет, что пользователь ввел правильный логин И правильный пароль — здесь работает функция AND, и только при выполнении обоих условий доступ будет предоставлен.
В системах автоматизации и умных устройствах обеспечивают логику работы «умного дома», автомобильных систем безопасности, промышленных контроллеров. Например, система климат-контроля включает кондиционер только тогда, когда температура превышает заданное значение ИЛИ влажность выше критического уровня — здесь применяется функция OR для обеспечения комфортных условий по любому из двух параметров.
Основные логические операции
Для понимания принципов работы булевых функций необходимо детально изучить основные логические операции. Каждая из них имеет свои особенности применения и четко определенные правила преобразования входных значений в выходные.
Операция AND (И, конъюнкция)
AND возвращает значение true только в том случае, когда все входные значения равны true. В булевой алгебре эту операцию также называют логическим умножением и обозначают символом ∧.
| A | B | A ∧ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Практическое применение: системы безопасности, где доступ предоставляется только при наличии корректной карты доступа И правильного PIN-кода.
Операция OR (ИЛИ, дизъюнкция)
OR возвращает true, если хотя бы один из входов равен true. Обозначается символом ∨ и называется логическим сложением.
| B | A ∨ B | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Операция NOT (НЕ, отрицание, инверсия)
Унарная операция NOT инвертирует входное значение — меняет true на false и наоборот. Обозначается символом ¬.
| A | ¬A |
| 0 | 1 |
| 1 | 0 |
Операция XOR (исключающее ИЛИ)
XOR возвращает true только когда входы различаются — один true, другой false.
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операции NAND и NOR
NAND (И-НЕ) и NOR (ИЛИ-НЕ) являются инвертированными версиями AND и OR соответственно. Особенность заключается в их функциональной полноте — любую булеву функцию можно выразить только через NAND или только через NOR.
NAND: | A | B | A ↑ B | |—|—|——-| | 0 | 0 | 1 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |
NOR: | A | B | A ↓ B | |—|—|——-| | 0 | 0 | 1 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 0 |
Таблица истинности: как она работает и как её построить
Таблица истинности — это систематический способ представления всех возможных комбинаций входных значений булевой функции и соответствующих им результатов. Можно сказать, что это своеобразная «карта», которая полностью описывает поведение логической операции во всех возможных ситуациях.
Что показывает таблица истинности? Таблица демонстрирует, какой результат выдаст функция для каждого возможного набора входных данных. Это особенно важно при разработке логических схем и отладке программного кода — мы получаем исчерпывающую информацию о поведении системы.
Количество строк в таблице определяется по формуле 2ⁿ, где n — количество переменных (входов). Для одной переменной получаем 2¹ = 2 строки, для двух переменных — 2² = 4 строки, для трех — 2³ = 8 строк, и так далее. Это экспоненциальный рост: уже при 10 переменных таблица будет содержать 1024 строки, что демонстрирует вычислительную сложность анализа больших логических систем.
Правильная организация столбцов следует определенной логике: сначала располагаются столбцы для всех входных переменных (обычно обозначаемых как A, B, C и т.д.), затем — столбец или столбцы для промежуточных вычислений (если функция сложная), и наконец — столбец с финальным результатом функции.
Зачем это нужно? Таблицы истинности служат нескольким важным целям: они позволяют проверить корректность логических выражений, помогают в оптимизации булевых функций, используются для синтеза логических схем и являются основой для формальной верификации алгоритмов. В области разработки ИИ-систем таблицы истинности помогают валидировать логику принятия решений нейронными сетями на простых случаях.
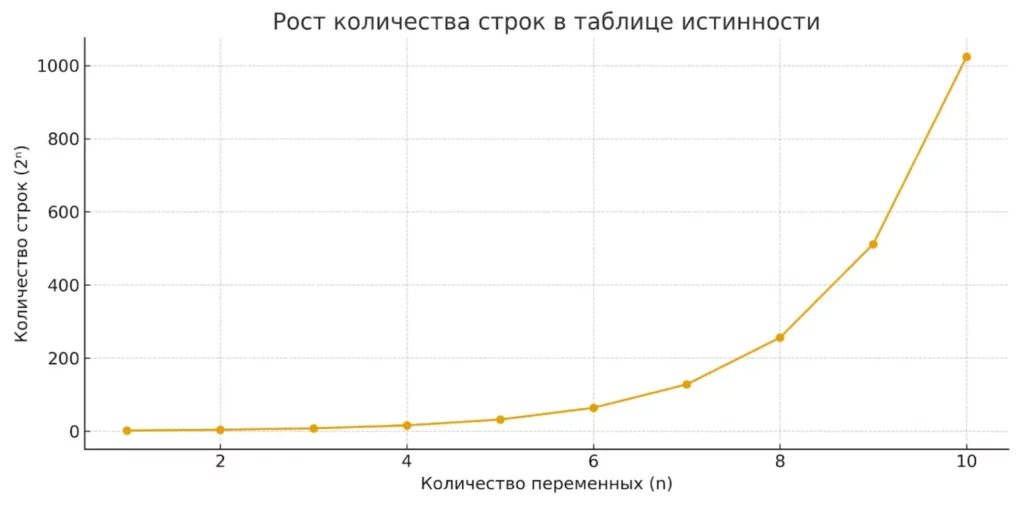
График показывает, как экспоненциально увеличивается число строк таблицы истинности при росте количества переменных. Уже при 10 переменных таблица содержит 1024 строки, что усложняет анализ.
Построение таблицы истинности — это систематический процесс, требующий внимательности и методичности, но овладев этим навыком, мы получаем мощный инструмент для анализа и проектирования логических систем любой сложности.
Пример составления таблицы истинности
Рассмотрим практический пример построения таблицы истинности для сложного логического выражения (A AND B) OR NOT(C). Этот пример наглядно демонстрирует, как работать с композицией нескольких булевых функций.
Шаг 1: Определение переменных
В нашем выражении присутствуют три переменные: A, B и C. Это означает, что таблица будет содержать 2³ = 8 строк для всех возможных комбинаций входных значений.
Шаг 2: Перебор всех комбинаций
Систематически перечисляем все возможные комбинации значений переменных от 000 до 111 в двоичной системе:
| A | B | C |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Шаг 3: Пошаговые вычисления
Строка 1 (A=0, B=0, C=0): A AND B = 0 AND 0 = 0; NOT(C) = NOT(0) = 1; Результат: 0 OR 1 = 1
Строка 2 (A=0, B=0, C=1): A AND B = 0 AND 0 = 0; NOT(C) = NOT(1) = 0; Результат: 0 OR 0 = 0
Строка 7 (A=1, B=1, C=0): A AND B = 1 AND 1 = 1; NOT(C) = NOT(0) = 1; Результат: 1 OR 1 = 1
Строка 8 (A=1, B=1, C=1): A AND B = 1 AND 1 = 1; NOT(C) = NOT(1) = 0; Результат: 1 OR 0 = 1
Анализируя полученную таблицу, мы видим, что выражение возвращает false только в случаях, когда C=1 и одновременно хотя бы одна из переменных A или B равна 0. Это демонстрирует, как сложные логические условия можно разложить на простые компоненты и проанализировать их поведение в различных ситуациях.
Суперпозиция булевых функций
Суперпозиция булевых функций представляет собой процесс объединения нескольких простых логических операций в сложные выражения. Этот механизм позволяет создавать многоуровневые логические структуры, которые лежат в основе современных вычислительных алгоритмов и систем принятия решений.
Что такое вложенность в булевых выражениях? Вложенность означает, что результат одной булевой функции становится входом для другой функции. Например, в выражении NOT(A AND B) сначала выполняется операция AND над переменными A и B, а затем к полученному результату применяется операция NOT. Таким образом, мы получаем функцию, эквивалентную NAND.
Порядок выполнения операций в булевой алгебре следует тем же принципам, что и в обычной математике: операции в скобках выполняются первыми, затем применяется приоритет операций (NOT имеет наивысший приоритет, затем AND, затем OR). Рассмотрим выражение A OR B AND NOT(C): здесь сначала вычисляется NOT(C), затем B AND NOT(C), и наконец A OR [результат предыдущей операции].
Пример со сложной формулой: рассмотрим выражение (A AND B) OR (NOT(A) AND C). Эта формула описывает логику, при которой результат истинен, если либо выполняются условия A и B одновременно, либо A ложно, но при этом выполняется условие C.
| A | B | C | A AND B | NOT(A) | NOT(A) AND C | Результат |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Понимание суперпозиции критически важно при разработке сложных систем: от простых условных конструкций в коде до архитектуры логических элементов в процессорах и даже логики работы нейронных сетей, где каждый нейрон можно рассматривать как сложную булеву функцию с множественными входами.
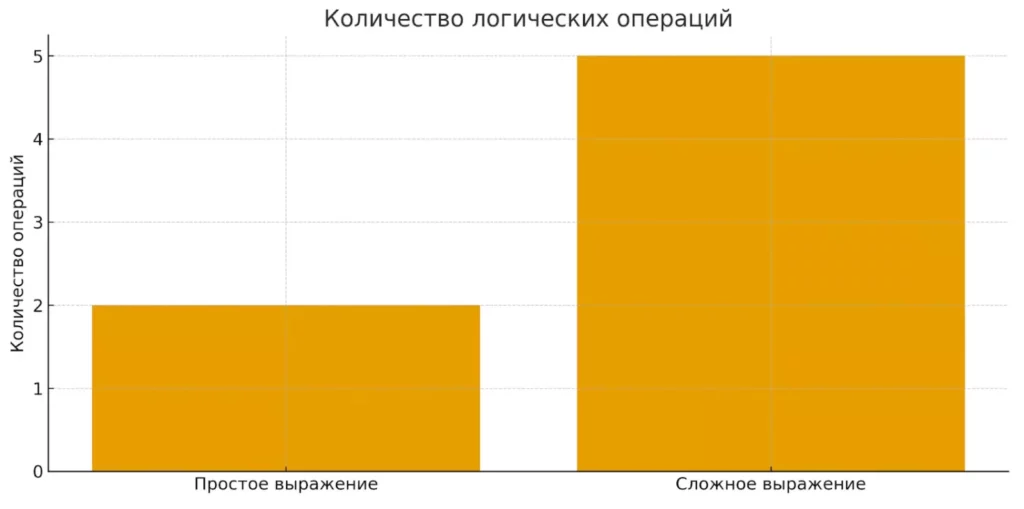
Столбчатая диаграмма иллюстрирует, как при усложнении выражения растёт число логических операций. Это подчёркивает важность оптимизации логических формул.
Двойственные булевы функции
Принцип двойственности в булевой алгебре представляет собой фундаментальное свойство, согласно которому каждая логическая функция имеет свою двойственную пару. Этот принцип не только демонстрирует элегантную симметрию булевой алгебры, но и служит мощным инструментом для оптимизации логических выражений.
Основные пары двойственных функций:
- AND (И) ↔ OR (ИЛИ) — наиболее фундаментальная пара
- XOR (исключающее ИЛИ) ↔ XNOR (исключающее ИЛИ-НЕ)
- NAND (И-НЕ) ↔ NOR (ИЛИ-НЕ)
Двойственная функция получается путем замены всех операций AND на OR и наоборот, а также инвертирования всех констант (0 становится 1, 1 становится 0). Например, если исходная функция имеет вид A AND (B OR 0), то её двойственная будет A OR (B AND 1).
| Исходная функция | Двойственная функция |
| A AND B | A OR B |
| A OR (B AND C) | A AND (B OR C) |
| NOT(A) AND 1 | NOT(A) OR 0 |
Применение в оптимизации: двойственные функции находят практическое применение при оптимизации логических схем и программного кода. Иногда двойственное представление функции может оказаться проще для реализации или требовать меньше вычислительных ресурсов.
Методы минимизации булевых выражений
Минимизация булевых выражений — это процесс упрощения логических функций с целью уменьшения количества операций, сохраняя при этом функциональность. В эпоху, когда эффективность вычислений критически важна для всего — от мобильных приложений до систем машинного обучения — владение методами оптимизации становится необходимым навыком.
Карты Карно
Метод карт Карно (или карт Вейча-Карно) представляет собой графический способ минимизации булевых функций. Основная идея заключается в преобразовании таблицы истинности в двумерную сетку, где соседние ячейки отличаются значением только одной переменной.
Алгоритм работы: размещаем значения функции в ячейки карты согласно кодировке Грея, затем объединяем соседние группы единиц в прямоугольники максимального размера. Каждый такой прямоугольник соответствует упрощенному терму в итоговом выражении.
Преимущества: интуитивно понятен, подходит для функций до 4-5 переменных. Недостатки: становится громоздким при большом количестве переменных.
Разложение Шеннона
Метод разложения Шеннона основан на рекурсивном разбиении булевой функции относительно выбранной переменной. Функция f(A,B,C) разлагается как: f = A·f₁ + ¬A·f₀, где f₁ — функция при A=1, f₀ — функция при A=0.
Применение: этот метод особенно эффективен для функций с большим количеством переменных и лежит в основе современных алгоритмов синтеза логических схем.
Преимущества: масштабируется на любое количество переменных, подходит для автоматизации. Недостатки: может приводить к экспоненциальному росту промежуточных выражений.
Метод Куайна и Куайна-Маккласки
Классический метод Куайна включает два этапа: сначала функцию приводят к сокращенному виду с помощью операций склеивания (объединения соседних термов) и поглощения (удаления избыточных термов), затем из сокращенной формы получают минимальную, удаляя переменные, не влияющие на результат.
Усовершенствованный метод Куайна-Маккласки систематизирует процесс склеивания, разделяя термы на группы по количеству единиц и проводя попарное сравнение только между соседними группами.
Преимущества: гарантирует нахождение минимальной формы, полностью алгоритмизирован. Недостатки: высокая вычислительная сложность для больших функций.
Метод Блейка-Порецкого
Этот метод основан на представлении булевых функций в виде троичных векторов и использовании специальных матриц для их преобразования. Подход позволяет работать с неопределенными значениями (don’t care) и эффективно обрабатывать частично заданные функции.
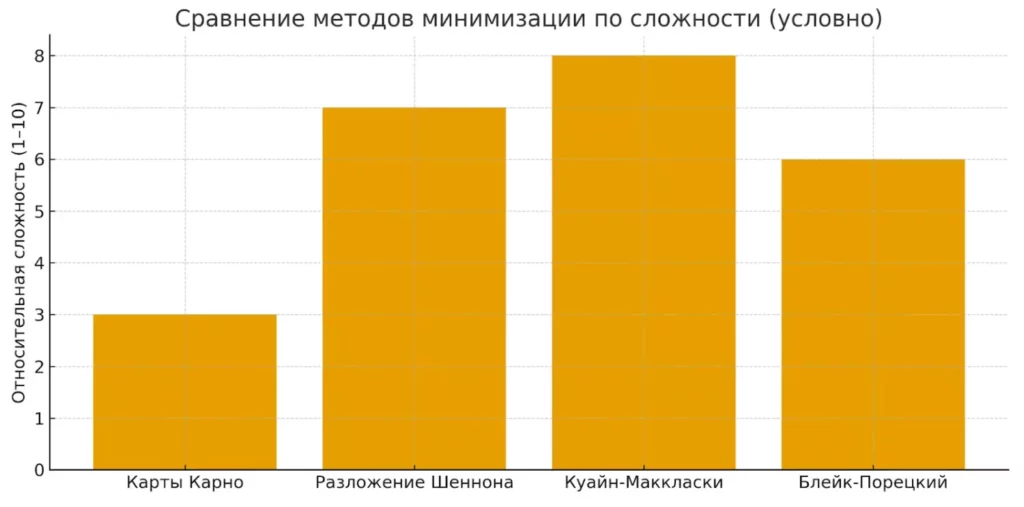
Диаграмма сравнивает популярные методы минимизации по условной сложности. Видно, что карты Карно проще для небольших задач, а Куайн-Маккласки — более трудоёмкий, но точный метод.
Современное применение: методы минимизации активно используются в CAD-системах для проектирования цифровых схем, компиляторах для оптимизации условных конструкций и даже в системах машинного обучения для упрощения логических правил, извлекаемых из нейронных сетей.
FAQ — Часто задаваемые вопросы
- Сколько максимально строк может быть в таблице истинности? Теоретически ограничений нет — количество строк равно 2ⁿ, где n — число переменных. Однако практически уже при 20 переменных получаем более миллиона строк, что делает ручной анализ невозможным. В реальных проектах функции с более чем 6-8 переменными требуют автоматизированных методов анализа.
- Что делать, если переменных слишком много для ручного построения таблицы? Используйте специализированные инструменты: программы типа Logisim для образовательных целей, профессиональные CAD-системы вроде Quartus или Vivado для разработки цифровых схем, либо пишите собственные скрипты на Python с использованием библиотек для символьных вычислений.
- Как автоматизировать построение и анализ таблиц истинности? Современные подходы включают использование Python-библиотек (sympy, itertools), специализированных языков описания аппаратуры (VHDL, Verilog) или онлайн-калькуляторов. Для сложных проектов рекомендуется изучение формальных методов верификации.
- Где они применяются в машинном обучении? В логических моделях (деревья решений), при создании признаков для нейронных сетей, в генетических алгоритмах и эволюционных вычислениях. Понимание булевой логики помогает создавать более интерпретируемые ИИ-системы.
- Нужно ли изучать их, если я не планирую заниматься разработкой схем? Абсолютно да. Булева алгебра — это основа логического мышления в программировании, базис для понимания алгоритмов и структур данных, а также фундамент для работы с базами данных, системами правил и многими другими областями IT.
Заключение
Изучение булевых функций открывает перед нами понимание фундаментальных принципов, на которых строится вся современная цифровая цивилизация. В ходе нашего обзора мы проследили путь от простейших логических операций до сложных методов оптимизации, демонстрирующих, как математическая строгость булевой алгебры превращается в практические инструменты разработки. Подведем итоги:
- Булевы функции описывают логику принятия решений. Они формализуют условия и сокращают неоднозначность в алгоритмах.
- Таблицы истинности показывают все комбинации входов и результатов. Они позволяют проверять корректность и находить ошибки в логике.
- Базовые операции AND, OR, NOT, XOR лежат в основе вычислительных систем. Они дают общий язык для схемотехники и кода.
- Наборы NAND/NOR функционально полны. Они упрощают аппаратную реализацию и уменьшают число элементов в схемах.
- Методы минимизации сокращают выражения без потери смысла. Они повышают скорость, уменьшают ресурсы и упрощают поддержку.
- Суперпозиция формирует сложные условия из простых. Она помогает проектировать многоуровневые правила и модули.
- Принцип двойственности связывает пары операций. Он открывает альтернативные эквивалентные формы для оптимизации.
- Знание булевой алгебры применимо от кода до ИИ. Оно делает решения прозрачнее и улучшает качество систем.
Рекомендуем обратить внимание на подборку курсов по разработке на Python, особенно если вы только начинаете осваивать профессию разработчика. В курсах предусмотрены и теоретические модули, и практические задания для закрепления знаний.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
83 отзыва
|
Цена
Ещё -5% по промокоду
95 000 ₽
|
От
7 917 ₽/мес
|
Длительность
6 месяцев
|
Старт
27 декабря
|
Ссылка на курс |
|
Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 января
|
Ссылка на курс |
|
Fullstack-разработчик на Python
|
Нетология
45 отзывов
|
Цена
с промокодом kursy-online
146 500 ₽
308 367 ₽
|
От
4 282 ₽/мес
|
Длительность
18 месяцев
|
Старт
1 января
|
Ссылка на курс |
|
Python-разработчик
|
Академия Синергия
34 отзыва
|
Цена
91 560 ₽
228 900 ₽
|
От
3 179 ₽/мес
4 552 ₽/мес
|
Длительность
6 месяцев
|
Старт
6 января
|
Ссылка на курс |
|
Профессия Python-разработчик
|
Skillbox
205 отзывов
|
Цена
Ещё -20% по промокоду
74 507 ₽
149 015 ₽
|
От
6 209 ₽/мес
9 715 ₽/мес
|
Длительность
12 месяцев
|
Старт
25 декабря
|
Ссылка на курс |

Как VR и AR меняют анимацию: технологии, примеры, перспективы
Слияние VR, AR и анимации уже изменило индустрию. Узнайте о ключевых технологиях, инструментах и проектах, которые задают новые стандарты.

Что такое SEO-верстка и как она влияет на продвижение сайта?
Грамотная SEO-верстка — это не только код, но и стратегия повышения видимости сайта в поиске. Узнайте, как она улучшает ранжирование и UX.

Java и Go: что выбрать для серверной разработки?
Задумываетесь, какой язык программирования лучше подходит для серверной разработки? В статье рассмотрены ключевые особенности Java и Go, чтобы помочь вам принять оптимальное решение.

Capture One против Lightroom: какой RAW-редактор выбрать
Capture One — это не просто RAW-конвертер. Узнайте, зачем его выбирают студийные фотографы, ретушеры и владельцы камер Sony, Fujifilm и Nikon.