Если вы когда-нибудь стояли между двумя зеркалами в ванной комнате, глядя на бесконечную последовательность отражений, уходящих в глубину, — поздравляю, вы уже знакомы с концепцией рекурсии. Или, как я люблю её называть, "программистским инцепшеном".
Говоря простым языком, рекурсия — это когда функция вызывает саму себя для решения меньшей версии той же проблемы. Это как матрёшка кода: внутри большой задачи находится такая же, но поменьше, а внутри неё — еще одна, и так до самой малюсенькой, которую можно решить напрямую.
Когда же рекурсия удобнее итерации (то есть обычных циклов)? Представьте, что вам нужно обойти все файлы в директории, включая вложенные папки. Можно, конечно, написать кучу вложенных циклов и поддерживать стек папок для посещения... Или просто сказать: "Для каждой папки просмотри все файлы, а если встретишь вложенную папку — сделай то же самое с ней". Вуаля! Мы только что описали рекурсивное решение, которое займёт пару строк кода вместо десятка.
Итак, вы решили погрузиться в кроличью нору рекурсии — поздравляю с этим отважным решением! Давайте разберемся, как это чудо компьютерной магии работает на самом деле, без лишней академической зауми.
Представьте, что рекурсивная функция — это сотрудник офиса, который для решения задачи вынужден клонировать самого себя. Каждый клон получает свой стол, свои документы и слегка измененное задание. Причем важно: оригинальный сотрудник не может продолжить работу, пока его клон не закончит свою часть и не вернет результат. В какой-то момент один из клонов получает настолько простую задачу, что может решить ее сам, без дальнейшего клонирования. Это и есть базовый случай.
Офисный сотрудник клонирует сам себя.
Любая уважающая себя рекурсивная функция состоит из двух ключевых элементов:
Базовый случай — условие, при котором функция возвращает результат напрямую, без дальнейших рекурсивных вызовов. Это как аварийный тормоз поезда, без которого мы бы неслись в бесконечность (читай: переполнение стека и болезненный краш программы).
Рекурсивный случай — когда функция вызывает саму себя, но с другими аргументами, постепенно "приближающимися" к базовому случаю. Это наш сотрудник, создающий клона для решения части задачи.
Схема работы рекурсивной функции:
┌───────────────────┐
│ function(params) │
└───────────┬───────┘
│
▼
┌─────────────────────┐ Да ┌───────────────┐
│ Это базовый случай? ├─────────►│ Вернуть ответ │
└─────────────┬───────┘ └───────────────┘
│ Нет
▼
┌─────────────────────────────┐
│ Изменить параметры │
└─────────────┬───────────────┘
│
▼
┌─────────────────────────────┐
│ function(новые_параметры) │
└─────────────────────────────┘
Базовый случай
Базовый случай — это фундамент вашей рекурсивной функции. Без него... ну, представьте, что вы сказали сотруднику: "Чтобы выполнить задачу A, надо сначала выполнить задачу A". Это как инструкция на бутылке шампуня: "Намылить, смыть, повторить" без указания, когда остановиться. Рано или поздно у вас закончится либо шампунь, либо терпение, либо память компьютера.
Пример ошибки без базового случая:
def countdown(n):
print(n)
countdown(n - 1) # Где останавливаться? Никто не знает!
Рекурсивный случай
В рекурсивном случае функция вызывает саму себя, но с "уменьшенной" проблемой. Критически важно, чтобы каждый рекурсивный вызов приближал нас к базовому случаю. Это как спускаться по лестнице — каждый шаг должен приближать вас к земле, а не уводить в стратосферу.
Например, если вы вычисляете факториал числа n, рекурсивный случай — это n * factorial(n-1). Мы уменьшаем n на 1 с каждым вызовом, что приближает нас к базовому случаю (когда n станет равно 1 или 0).
Визуализация стека вызовов
Представьте стопку документов на столе. Каждый раз, когда функция вызывает себя, на стопку кладется новый документ. Функция всегда работает с верхним документом. Когда она завершается, документ убирается, и функция возвращается к предыдущему.
Стек при вычислении factorial(3):
┌─────────────────┐
│ factorial(3) │ ◄ Получил результат factorial(2) = 2, вычисляет 3*2
└─────────────────┘
Результат: 6
Вот и весь фокус! Как видите, в рекурсии нет никакой черной магии — просто функция, которая знает, когда остановиться (базовый случай) и как себя "уменьшить" (рекурсивный случай). Главное — помнить, что каждый рекурсивный вызов занимает место в стеке, и если их будет слишком много — программа может упасть с криком "Stack overflow!" (что в среде программистов является не только ошибкой, но и названием сайта, куда они ходят, чтобы узнать, почему их код не работает).
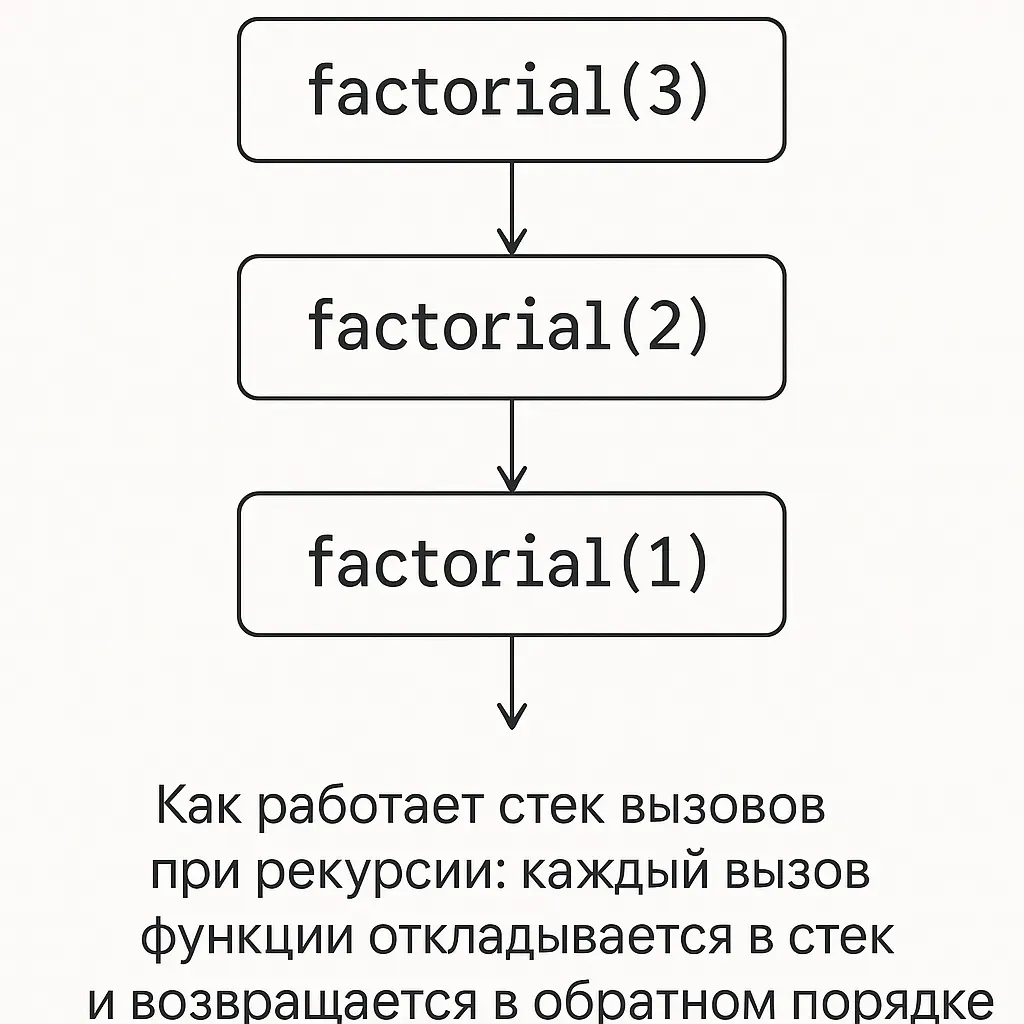
Как работает стек вызовов при рекурсии: каждый вызов функции откладывается в стек и возвращается в обратном порядке.
Простой пример: сумма чисел от 1 до N
Давайте перейдем от теории к практике и рассмотрим простейший пример рекурсии — вычисление суммы чисел от 1 до N. Конечно, для этой задачи существует изящная математическая формула (N*(N+1)/2), но где тогда веселье от программирования?
Представим, что мы хотим написать функцию sum(n), которая считает сумму 1+2+3+...+n. Как мыслит рекурсивно ориентированный мозг? Примерно так: "Сумма чисел от 1 до n — это n плюс сумма чисел от 1 до (n-1)". Звучит почти как определение из учебника, не правда ли?
def recursive_sum(n):
# Базовый случай: если n = 1, то сумма равна 1
if n == 1:
return 1
# Рекурсивный случай: sum(n) = n + sum(n-1)
else:
return n + recursive_sum(n - 1)
# Проверим на примере
print(recursive_sum(5)) # Должно вывести 15 (1+2+3+4+5)
Что происходит при вызове recursive_sum(5)? Давайте пройдемся пошагово, как будто мы — компьютер:
Вызываем recursive_sum(5). Это не базовый случай, поэтому возвращаем 5 + recursive_sum(4).
Но сначала нужно вычислить recursive_sum(4). Это не базовый случай, поэтому возвращаем 4 + recursive_sum(3).
Теперь нужно вычислить recursive_sum(3). Опять не базовый случай, поэтому 3 + recursive_sum(2).
Для recursive_sum(2) получаем 2 + recursive_sum(1).
Наконец, recursive_sum(1) — это базовый случай! Возвращаем 1.
Теперь начинаем "подниматься" обратно, подставляя полученные значения:
А что с производительностью? Для такой простой задачи рекурсивное решение проигрывает итеративному как по скорости, так и по памяти. Каждый рекурсивный вызов добавляет фрейм в стек вызовов, что требует дополнительной памяти. Если n будет большим (скажем, 10000), вы рискуете получить ошибку переполнения стека, в то время как цикл справится с этим без проблем.
Но не спешите хоронить рекурсию — в следующих примерах мы увидим, где она реально блистает!
Сравнение рекурсии и итерации
Если вы когда-нибудь оказывались на программистском корпоративе (эта странная вечеринка, где люди спорят о табах против пробелов с тем же пылом, с каким другие обсуждают футбольные матчи), то наверняка слышали жаркие дебаты: "Рекурсия или итерация? Что лучше?". Эта битва титанов заслуживает более пристального рассмотрения — без фанатизма, но с щепоткой здорового скептицизма.
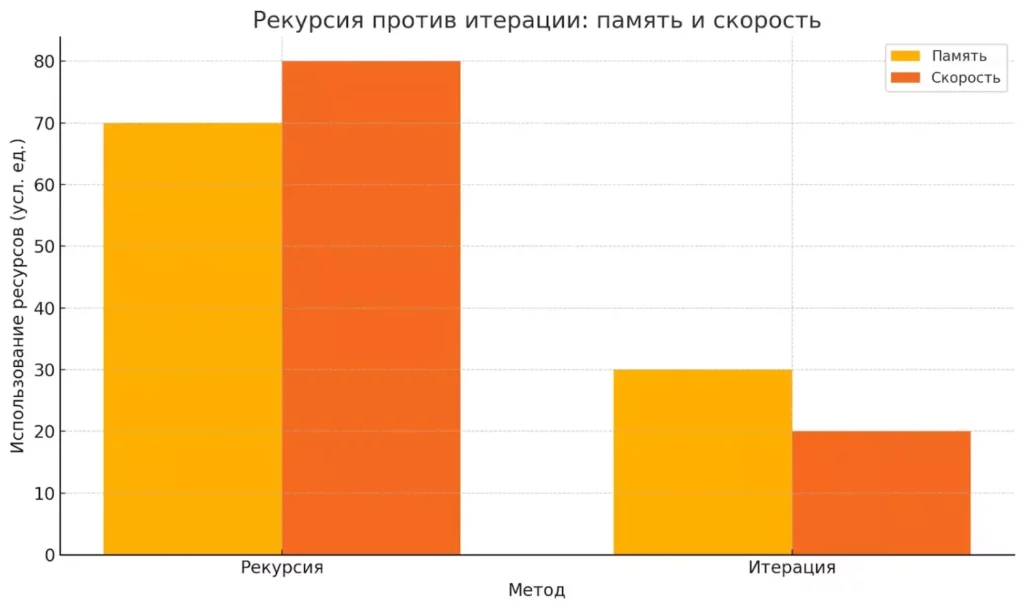
Сравнение использования ресурсов: рекурсия требует больше памяти и работает медленнее по сравнению с итерацией
Для наглядности давайте рассмотрим нашу старую знакомую — задачу вычисления суммы чисел от 1 до N — и решим её обоими способами:
# Рекурсивный подход
def recursive_sum(n):
if n == 1: # Базовый случай
return 1
else: # Рекурсивный случай
return n + recursive_sum(n - 1)
# Итеративный подход
def iterative_sum(n):
result = 0
for i in range(1, n + 1):
result += i
return result
Поразительно, насколько по-разному эти функции решают одну и ту же задачу! Рекурсивный вариант больше похож на математическое определение: "сумма от 1 до n — это n плюс сумма от 1 до (n-1)". Итеративный же больше похож на то, как человек посчитал бы сумму вручную: "начинаем с нуля и последовательно прибавляем каждое число".
Давайте сравним их в удобной таблице (я обожаю таблицы, они создают иллюзию, что я знаю, о чём говорю):
Критерий
Рекурсия
Итерация
Ясность кода
Часто более интуитивна для задач с естественной рекурсивной структурой
Обычно понятнее для линейных процессов
Использование памяти
Каждый вызов добавляет запись в стек — потенциальное переполнение
Требует только память для переменных цикла и результата
Скорость выполнения
Дополнительные накладные расходы на вызовы функций
Обычно быстрее из-за отсутствия накладных расходов
Элегантность
Часто приводит к более короткому и выразительному коду
Может стать громоздким в сложных случаях
Дебаггинг
Сложнее отлаживать из-за неочевидного потока выполнения
Проще визуализировать и отслеживать
Вот что интересно: в Python есть ограничение на глубину рекурсии (по умолчанию 1000), чтобы предотвратить переполнение стека. Это значит, что если вы попытаетесь вычислить recursive_sum(1001), программа аварийно завершится с RecursionError. Итеративная версия легко справится даже с iterative_sum(1000000), хотя это займет некоторое время.
С другой стороны, есть задачи, где рекурсия читается настолько естественнее, что стоит пожертвовать производительностью ради ясности. Типичный пример — обход древовидных структур: там рекурсивный код получается в разы компактнее и понятнее.
Важно понимать: нет "лучшего" способа для всех случаев. Выбор между рекурсией и итерацией — это как выбор между вилкой и палочками для еды. Для спагетти вилка удобнее, для суши — палочки, а для супа вообще нужна ложка. Инструменты должны соответствовать задаче.
Мой личный подход (основанный на горьком опыте и некотором количестве бессонных ночей): если задача естественно рекурсивна, и глубина рекурсии ограничена разумными пределами — используйте рекурсию. В противном случае итерация обычно будет более надёжным выбором. И помните главное правило программиста: "Сначала сделайте так, чтобы работало, потом — чтобы работало правильно, и только потом — чтобы работало быстро".
Пример 2: факториал числа
Если вы когда-нибудь имели несчастье общаться с математиками (я вот имел, у меня до сих пор нервный тик после разговоров о топологии), то наверняка слышали про факториал. Для непосвященных: факториал числа n (обозначается n!) — это произведение всех целых чисел от 1 до n включительно.
Например, 5! = 5 × 4 × 3 × 2 × 1 = 120.
Факториал — это классический пример задачи, которая так и напрашивается на рекурсивное решение. Почему? Да потому что его определение само по себе рекурсивно: n! = n × (n-1)!. И базовый случай тут очевиден: 1! = 1 (а также 0! = 1, хотя это уже из области математической магии).
Давайте реализуем это на Python:
def factorial(n):
# Базовый случай: 0! и 1! равны 1
if n <= 1:
return 1
# Рекурсивный случай: n! = n * (n-1)!
else:
return n * factorial(n - 1)
Пройдемся по шагам, чтобы понять, как это работает, на примере factorial(4):
Вызываем factorial(4). 4 > 1, поэтому возвращаем 4 * factorial(3).
Для вычисления factorial(3) возвращаем 3 * factorial(2).
Для factorial(2) получаем 2 * factorial(1).
factorial(1) — это базовый случай, возвращаем 1.
Подставляем значения в обратном порядке:
factorial(2) = 2 * 1 = 2
factorial(3) = 3 * 2 = 6
factorial(4) = 4 * 6 = 24
Таким образом, factorial(4) = 24, что соответствует 4! = 4 × 3 × 2 × 1 = 24.
Как и в случае с суммой, факториал можно вычислить итеративно:
def factorial_iterative(n):
result = 1
for i in range(2, n + 1):
result *= i
return result
Что интересно, для вычисления факториала большинство программистов выбирают именно итеративный подход, потому что:
Он не ограничен глубиной рекурсии (попробуйте вычислить factorial(1000) рекурсивно — Python выбросит RecursionError).
Он работает быстрее, так как не тратит ресурсы на вызовы функций.
Однако я всё равно считаю, что рекурсивное определение факториала элегантнее. Оно лучше отражает математическую суть проблемы. И если вы пишете код, который будет читать другой человек (или вы сами через полгода, когда уже забудете всё, что делали), то ясность намерения может быть важнее производительности.
И еще одно наблюдение: обе версии функции фактически выполняют одни и те же операции умножения, просто в разном порядке. Рекурсивная версия перемножает числа "в обратном порядке" (сначала меньшие), а итеративная — "в прямом" (начиная с больших). Результат, конечно, от этого не меняется, но это интересная деталь, показывающая разницу в подходах.
А знаете, что еще интересно? В Python есть встроенная функция для вычисления факториала в модуле math: math.factorial(). И она, скорее всего, реализована итеративно для максимальной производительности. Так что если вам нужен факториал в реальном проекте, лучше использовать её. Всё-таки жизнь слишком коротка, чтобы изобретать велосипед каждый раз (если только это не учебный проект, конечно).
Пример 3: проверка палиндрома
Палиндром — это слово, фраза или число, которое читается одинаково слева направо и справа налево. Примеры палиндромов: "шалаш", "топот", "А роза упала на лапу Азора", 12321. Задача проверки палиндрома — один из тех случаев, когда рекурсивное решение особенно элегантно иллюстрирует принцип "от внешнего к внутреннему".
Логика палиндрома рекурсивна по своей природе: строка является палиндромом, если ее первый и последний символы совпадают, а подстрока между ними тоже является палиндромом. Это чем-то напоминает матрешку — снаружи всё должно совпадать, чтобы можно было проверить следующий уровень вложенности.
Вот как выглядит рекурсивная функция проверки палиндрома:
def is_palindrome(s):
# Удаляем пробелы и приводим к нижнему регистру для более гибкой проверки
s = s.lower().replace(" ", "")
# Базовый случай 1: пустая строка или строка из одного символа - палиндром
if len(s) <= 1:
return True
# Базовый случай 2: если первый и последний символы различаются - не палиндром
if s[0] != s[-1]:
return False
# Рекурсивный случай: проверяем, является ли центральная часть палиндромом
return is_palindrome(s[1:-1])
Представьте, как это работает на примере слова "шалаш":
Первый вызов is_palindrome("шалаш"):
Первый символ "ш" равен последнему "ш"? Да.
Проверяем внутреннюю часть: is_palindrome("ала")
Второй вызов is_palindrome("ала"):
Первый символ "а" равен последнему "а"? Да.
Проверяем внутреннюю часть: is_palindrome("л")
Третий вызов is_palindrome("л"):
Строка из одного символа — это базовый случай, возвращаем True
Возвращаемся ко второму вызову, который теперь тоже возвращает True
Наконец, первый вызов тоже возвращает True — слово "шалаш" действительно палиндром!
Конечно, в Python для такой задачи существует гораздо более лаконичное решение без рекурсии:
def is_palindrome_simple(s):
s = s.lower().replace(" ", "")
return s == s[::-1] # Сравниваем строку с ее обратной версией
Однако рекурсивное решение лучше иллюстрирует логику проверки "от краев к центру" и демонстрирует важную концепцию: иногда рекурсия позволяет выразить алгоритм в терминах, которые ближе к человеческому пониманию проблемы.
Интересный момент: рекурсивное решение, возможно, медленнее и требует больше памяти, но оно гораздо ближе к тому, как бы человек вручную проверял палиндром. Мы обычно не переворачиваем всё слово целиком (как делает строковый срез s[::-1]), а проверяем парами символы с обоих концов.
Если задуматься, это отличная иллюстрация того, что иногда более "человеческий" алгоритм не самый эффективный с точки зрения компьютера. Эта дихотомия между "понятностью для человека" и "эффективностью для машины" — одна из фундаментальных в программировании, и рекурсия часто находится где-то посередине этого спектра.
Пример 4: обход вложенных списков
Теперь давайте перейдем к задаче, где рекурсия действительно начинает блистать — к обходу вложенных структур данных. Представьте, что у вас есть список, элементами которого могут быть как обычные значения, так и другие списки (которые, в свою очередь, тоже могут содержать списки). Что-то вроде этого:
Допустим, вам нужно подсчитать сумму всех числовых элементов в этой структуре. С итерацией это... ну, мягко говоря, непросто. Вам пришлось бы использовать стек или очередь для отслеживания вложенности, и код получился бы достаточно запутанным. С рекурсией же решение практически напрашивается само собой.
Вот рекурсивная функция для подсчета суммы всех элементов во вложенном списке:
def sum_nested_list(nested_list):
total = 0
for item in nested_list:
if isinstance(item, list):
# Если элемент -- список, рекурсивно суммируем его содержимое
total += sum_nested_list(item)
else:
# Если элемент -- число, просто добавляем его к сумме
total += item
return total
# Пример использования
nested_list = [1, 2, [3, 4, [5, 6]], 7, [8, [9, 10]]]
print(sum_nested_list(nested_list)) # Должно вывести 55 (1+2+3+4+5+6+7+8+9+10)
Суть функции проста:
Проходим по каждому элементу списка.
Если элемент сам является списком, рекурсивно вызываем ту же функцию для него.
Если элемент — обычное число, добавляем его к итоговой сумме.
Что происходит при вызове sum_nested_list([1, 2, [3, 4, [5, 6]], 7, [8, [9, 10]]])? Давайте пройдемся по ключевым шагам:
Попробуйте представить, как бы выглядел итеративный вариант этой функции. Вам пришлось бы:
Использовать стек для хранения элементов, которые нужно обработать
Явно отслеживать, какие списки уже обработаны, а какие ещё нет
Разбираться с множеством условий и переходов
Важно отметить: не всегда то, что выглядит как вложенная структура, лучше обрабатывать рекурсивно. Например, JSON-данные могут быть глубоко вложенными, но если их структура известна заранее, иногда проще использовать прямой доступ к нужным полям. Рекурсия блистает именно тогда, когда структура может быть произвольной и неизвестной заранее.
Пример 5: быстрая сортировка (quicksort)
Если вы когда-нибудь погружались в мир алгоритмов сортировки глубже, чем пузырьковая сортировка на первом курсе, то наверняка встречали "быструю сортировку" (quicksort) — один из самых элегантных и эффективных алгоритмов сортировки, основанных на рекурсии. Этот алгоритм был разработан британским ученым Тони Хоаром еще в 1959 году, и с тех пор он остается одним из фаворитов в мире программирования.
Принцип действия quicksort основан на методе "разделяй и властвуй" (divide and conquer) и включает в себя три основных шага:
Выбор опорного элемента (pivot) из массива
Разделение массива на два подмассива: элементы, которые меньше опорного, и элементы, которые больше опорного
Рекурсивное применение алгоритма к обоим подмассивам
Звучит довольно просто, правда? Давайте реализуем это на Python:
def quicksort(arr):
# Базовый случай: пустой список или список из одного элемента уже отсортирован
if len(arr) <= 1:
return arr
# Выбираем опорный элемент (для простоты берем средний элемент)
pivot = arr[len(arr) // 2]
# Разделяем массив на три части: меньше, равно и больше опорного
left = [x for x in arr if x < pivot] # Элементы меньше опорного
middle = [x for x in arr if x == pivot] # Элементы равные опорному
right = [x for x in arr if x > pivot] # Элементы больше опорного
# Рекурсивно сортируем подмассивы и объединяем результаты
return quicksort(left) + middle + quicksort(right)
Теперь давайте пошагово пройдемся по работе алгоритма на примере списка [7, 2, 1, 6, 8, 5, 3, 4]:
Первый вызов quicksort([7, 2, 1, 6, 8, 5, 3, 4]):
Опорный элемент: 6 (средний элемент массива)
Разделение:
left = [2, 1, 5, 3, 4] (элементы меньше 6)
middle = [6] (элементы, равные 6)
right = [7, 8] (элементы больше 6)
Рекурсивно сортируем left и right
Вызов quicksort([2, 1, 5, 3, 4]):
Опорный элемент: 3
Разделение:
left = [2, 1]
middle = [3]
right = [5, 4]
Рекурсивно сортируем left и right
Вызов quicksort([2, 1]):
Опорный элемент: 2
Разделение:
left = [1]
middle = [2]
right = []
[1] и [] - базовые случаи, просто возвращаем
... и так далее, пока все подмассивы не будут отсортированы.
Этап
Описание
Результат
1
Выбор опорного элемента
Обычно выбирают первый, последний или средний элемент. В реальных реализациях часто используют медиану из трех элементов для лучшей производительности.
2
Разделение
Группировка элементов на "меньше опорного", "равные опорному" и "больше опорного". Это ключевой шаг, от которого зависит эффективность алгоритма.
3
Рекурсивная сортировка
Применение того же алгоритма к подмассивам, пока все элементы не будут отсортированы.
4
Объединение
Соединение отсортированных подмассивов в правильном порядке.
Выбор опорного элемента критически важен для производительности quicksort. В худшем случае (когда массив уже отсортирован, а в качестве опорного выбирается первый элемент) сложность алгоритма может достигать O(n²). Однако в среднем случае quicksort работает со сложностью O(n log n), что делает его одним из самых быстрых алгоритмов сортировки.
Обратите внимание, что наша реализация не самая оптимальная с точки зрения использования памяти, поскольку она создает новые списки на каждом шаге. В реальных приложениях часто используется "in-place" версия, которая сортирует массив на месте, без создания дополнительных копий.
Когда использовать рекурсию
Как и любой мощный инструмент в арсенале программиста, рекурсия требует рассудительного применения. Это как молоток — незаменим для забивания гвоздей, но совершенно неуместен, когда нужно закрутить шуруп. Давайте разберёмся, когда стоит выбирать рекурсивный подход, а когда лучше обратиться к другим методам.
Рекурсия уместна, когда:
Задача естественно разбивается на подзадачи того же типа.
Работаете с рекурсивными структурами данных.
Решаете задачи со структурой "разделяй и властвуй".
Важна читаемость кода.
Глубина рекурсии ограничена и предсказуема.
Если вы заранее знаете, что глубина вызовов не превысит разумных пределов (скажем, глубину сбалансированного бинарного дерева).
Рекурсию лучше не использовать, когда:
Глубина рекурсии может быть большой или непредсказуемой. Риск столкнуться с ошибкой переполнения стека слишком высок.
Производительность критически важна. Накладные расходы на создание и поддержание стека вызовов могут существенно снизить скорость работы.
Задача легко решается итеративно. Если итеративное решение не менее ясно и более эффективно, нет смысла прибегать к рекурсии.
Работаете в среде с ограниченными ресурсами. В микроконтроллерах или системах с ограниченной памятью рекурсия может быть непозволительной роскошью.
Реализуете алгоритмы динамического программирования. Хотя их можно записать рекурсивно, итеративный подход с мемоизацией обычно эффективнее.
Золотые правила работы с рекурсией:
Всегда определяйте базовый случай. Это ваша страховка от бесконечной рекурсии.
Убедитесь, что каждый рекурсивный вызов приближает вас к базовому случаю. Если вы топчетесь на месте, рано или поздно стек переполнится.
Рассмотрите возможность мемоизации для задач с перекрывающимися подзадачами. Кэширование результатов предыдущих вызовов может радикально улучшить производительность.
Будьте осторожны с аргументами по умолчанию. В Python их значения вычисляются только при определении функции, что может привести к неожиданным эффектам (особенно с изменяемыми объектами).
Имейте запасной план. Если глубина рекурсии может превысить лимит Python, будьте готовы к реализации итеративного варианта.
Частые ошибки при работе с рекурсией
Давайте рассмотрим самые распространённые грабли, на которые наступают даже опытные программисты.
Отсутствие базового случая
Это классика жанра — забыть определить, когда рекурсия должна остановиться. Это примерно как забыть тормоза в автомобиле — поначалу всё идёт отлично, а потом... бум!
# Как НЕ надо делать
def countdown(n):
print(n)
countdown(n - 1) # Будет выполняться, пока Python не выбросит RecursionError
# Как надо
def countdown_correct(n):
print(n)
if n > 0: # Базовый случай!
countdown_correct(n - 1)
Бесконечная рекурсия
Даже если у вас есть базовый случай, нужно убедиться, что вы к нему действительно движетесь с каждым вызовом. Иначе вы попадёте в логический эквивалент беговой дорожки — много движения, но никакого прогресса.
# Опасно: аргумент не меняется
def infinite_recursion(n):
if n == 0:
return 0
else:
return 1 + infinite_recursion(n) # Упс, n не уменьшается!
# Неочевидный случай: недостаточное изменение
def gcd_wrong(a, b):
if b == 0:
return a
return gcd_wrong(a - b, b) # Если a < b, никогда не достигнем базового случая
Переполнение стека
Даже если ваша рекурсия правильно движется к базовому случаю, она может потребовать слишком много вложенных вызовов. В Python есть ограничение на глубину рекурсии (по умолчанию 1000), и превышение этого лимита приводит к ошибке.
# Слишком глубокая рекурсия
def factorial(n):
if n <= 1:
return 1
return n * factorial(n - 1)
try:
result = factorial(1500) # RecursionError: maximum recursion depth exceeded
except RecursionError as e:
print(f"Упс: {e}")
Неэффективная рекурсия
Некоторые рекурсивные функции многократно пересчитывают одни и те же значения, что приводит к экспоненциальному росту времени выполнения.
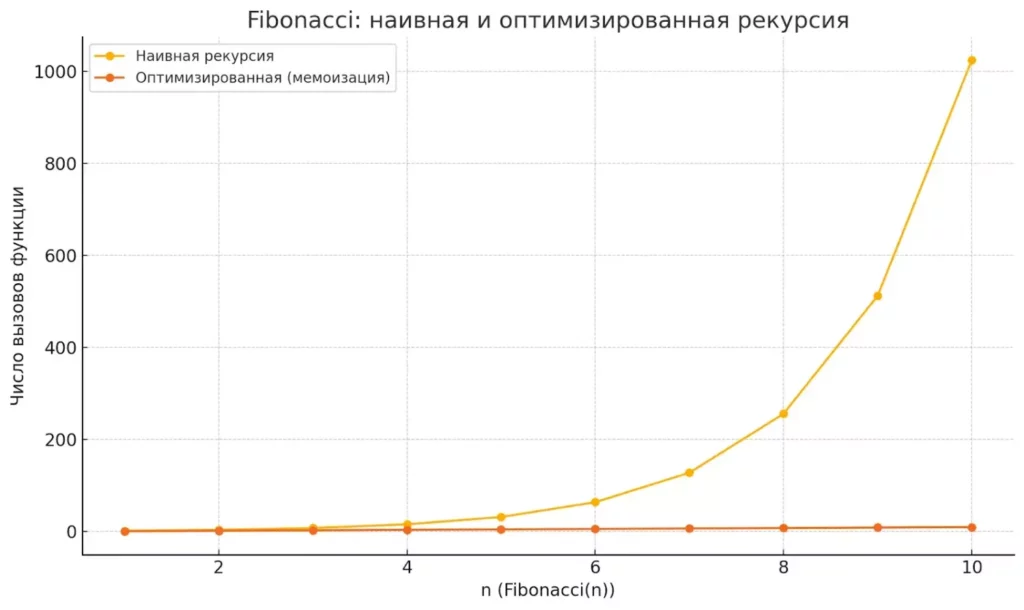
Количество вызовов при вычислении Fibonacci(n): наивная рекурсия вызывает экспоненциальное количество функций, тогда как оптимизированный подход — линейное.
# Классический пример неэффективной рекурсии
def fibonacci_naive(n):
if n <= 1:
return n
return fibonacci_naive(n - 1) + fibonacci_naive(n - 2) # Каждый вызов порождает два новых
# Для fibonacci_naive(5) функция будет вызвана 15 раз!
# А для fibonacci_naive(50) -- миллиарды раз (не пробуйте это дома)
Неожиданное поведение с изменяемыми объектами
Рекурсия и изменяемые объекты (особенно в аргументах по умолчанию) — гремучая смесь, которая может привести к трудноуловимым багам.
# Ловушка с аргументом по умолчанию
def accumulate(n, results=[]): # results инициализируется ОДИН раз при определении функции!
results.append(n)
if n >= 10:
return results
return accumulate(n + 1, results) # Один и тот же список используется при каждом вызове
print(accumulate(1)) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(accumulate(1)) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] -- упс!
Эти ошибки могут превратить элегантное рекурсивное решение в причину бессонных ночей и употребления чрезмерного количества кофеина. Избегайте их, придерживаясь золотых правил рекурсии, которые мы обсуждали ранее, и всегда помните: хорошая рекурсия — это рекурсия, которая знает, когда остановиться, и эффективно продвигается к этому моменту.
И еще один совет: если вы подозреваете проблемы с рекурсией, добавьте отладочный вывод с уровнем вложенности — это поможет визуализировать, что происходит внутри вашей программы, и быстрее найти источник проблемы.
Заключение
Рекурсия — это мощный инструмент программирования, который позволяет решать сложные задачи элегантно и выразительно. Понимание ее принципов — базового случая, рекурсивного случая и стека вызовов — открывает новый уровень мышления о проблемах и их решениях. Подведем итоги:
Базовый случай, рекурсивный случай и стек вызовов— три кита, на которых строится любая рекурсивная функция.
Рекурсивные решения особенно эффективны для задач с вложенной или самоподобной структурой, например при вычислении факториала, обходе дерева, работе с вложенными списками или реализации быстрой сортировки.
Код на рекурсии часто получается более читаемым, особенно в алгоритмах с естественной вложенностью.
Ограничения рекурсии — повышенное потребление памяти (из-за стека вызовов), потенциальная ошибка переполнения стека, сложность отладки и профилирования.
Не всегда стоит использовать рекурсию, итеративный подход зачастую быстрее и надёжнее при линейных задачах.
Золотые правила работы с рекурсией: всегда определяйте базовый случай, убедитесь, что каждый вызов приближает к выходу, контролируйте глубину рекурсии, используйте мемоизацию при повторяющихся вычислениях.
Если хотите прокачать свои скиллы в айти, то посмотрите курсы по Python. Собрали для вас подборку лучших, так что выбирайте тот, что по душе.
Low-code специалист — кто это и почему такие сотрудники всё чаще нужны бизнесу? Разбираем, какие задачи можно автоматизировать без классической разработки, какие навыки понадобятся и с чего начать обучение.
Хотите разобраться, как пользоваться GoLand и выжать максимум из IDE? В статье — простое объяснение ключевых функций, скрытых возможностей и рабочих приёмов, которые пригодятся как новичкам, так и опытным Go-разработчикам.
Мы используем cookies: необходимые — для работы сайта, а дополнительные — для аналитики и улучшения сервиса.
Можно принять все cookies, отклонить дополнительные или оставить только необходимые.
Подробнее
Говоря простым языком, рекурсия — это когда функция вызывает саму себя для решения меньшей версии той же проблемы. Это как матрёшка кода: внутри большой задачи находится такая же, но поменьше, а внутри неё — еще одна, и так до самой малюсенькой, которую можно решить напрямую.
Когда же рекурсия удобнее итерации (то есть обычных циклов)? Представьте, что вам нужно обойти все файлы в директории, включая вложенные папки. Можно, конечно, написать кучу вложенных циклов и поддерживать стек папок для посещения... Или просто сказать: "Для каждой папки просмотри все файлы, а если встретишь вложенную папку — сделай то же самое с ней". Вуаля! Мы только что описали рекурсивное решение, которое займёт пару строк кода вместо десятка.
