Округление в Python: что это и как работает
В мире программирования округление чисел — это не просто математическая операция, а необходимый инструмент для решения множества практических задач. Когда мы работаем с десятичными дробями, особенно в Python, мы часто сталкиваемся с проблемой точности вычислений. Казалось бы, простая операция 0.1 + 0.2 должна дать ровно 0.3, но на практике мы получаем 0.30000000000000004. Подобные неточности могут накапливаться и приводить к серьезным ошибкам в вычислениях, если не применять корректное округление. В этом курсе разберём, почему возникают ошибки при вычислениях, какие методы округления доступны в Python, и как выбрать подходящий способ для разных задач — от финансовых расчётов до обработки пользовательского ввода.

Также рассмотрим функции round(), Decimal, math.floor() и math.ceil(), сравним их поведение и особенности применения, а также покажем практические примеры, где корректное округление критично для стабильности работы программы.
- Зачем нужно округлять числа в Python
- Почему это не так просто
- Все способы rounding в Python
- Форматирование строк для округления вывода
- Какой метод выбрать в зависимости от задачи
- Частые ошибки и как их избежать
- Заключение
- Рекомендуем посмотреть курсы по Python
Зачем нужно округлять числа в Python
Представьте, что вы рассчитываете финансовые показатели, где даже копейка имеет значение, или обрабатываете научные данные, где точность измерений критична. В таких случаях неправильное округление может исказить результаты и привести к ошибочным выводам.
Rounding необходимо в следующих областях:
- Финансы и бухгалтерия — где точность в расчетах валют и процентов имеет юридическое значение, а ошибки могут привести к финансовым потерям или даже судебным разбирательствам.
- Медицина и фармацевтика — при расчете дозировок лекарств, где даже малейшая погрешность недопустима.
- Инженерные расчеты — где необходимо учитывать допуски и соблюдать технические спецификации.
- Статистика и аналитика данных — для корректного представления результатов и предотвращения накопления ошибок при обработке больших объемов информации.
- Визуализация данных — для упрощения восприятия числовой информации человеком.
- Разработка игр — для оптимизации вычислений физики или механики игрового процесса.
История знает немало примеров, когда неправильное rounding приводило к серьезным последствиям: от ракет, сбившихся с курса, до многомиллионных финансовых ошибок. Именно поэтому понимание принципов и методов округления в Python — необходимый навык для каждого разработчика, работающего с числовыми данными.
Почему это не так просто
В идеальном мире математических абстракций числа могут иметь бесконечную точность. Однако в реальности компьютерных вычислений мы сталкиваемся с фундаментальными ограничениями, заложенными в самой архитектуре компьютеров. Python, как и большинство языков программирования, использует формат с плавающей запятой (IEEE 754) для представления дробных чисел, что порождает ряд неочевидных проблем.
Основная сложность заключается в том, что компьютеры работают в двоичной системе счисления, где некоторые десятичные дроби, привычные нам, не могут быть представлены конечным числом битов. Например, простая дробь 1/10 (или 0.1 в десятичной записи) в двоичной системе представляется как бесконечная последовательность: 0.0001100110011001100…
Проиллюстрируем эту проблему на простом примере:
x = 0.1 + 0.2 print(x) # Ожидаем 0.3, но получаем 0.30000000000000004 print(x == 0.3) # False, хотя математически это должно быть True
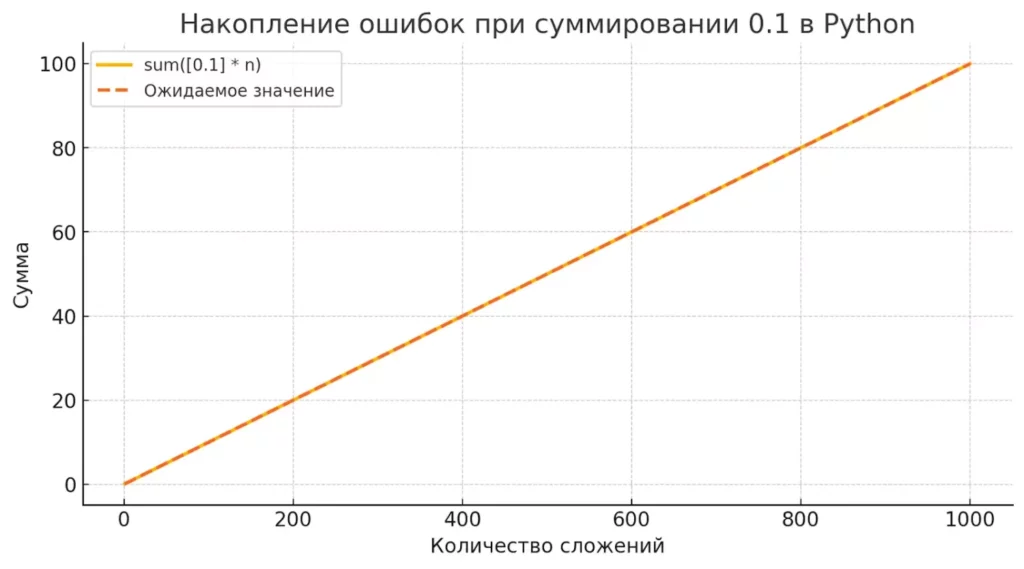
Накопление ошибок при сложении числа 0.1 в Python. Видно, как с ростом количества операций результат всё сильнее отклоняется от ожидаемого значения из-за особенностей представления чисел с плавающей запятой.
Еще более неожиданное поведение можно наблюдать при суммировании большого количества одинаковых чисел:
sum_result = sum([0.1] * 1000) print(sum_result) # 99.9999999999986 вместо ожидаемых 100.0
Эти маленькие погрешности могут накапливаться и приводить к существенным отклонениям в результатах вычислений. Особенно коварно это проявляется в финансовых расчетах или при сравнении результатов вычислений на равенство.
Другая проблема связана с особенностями реализации округления в Python. Рассмотрим следующий пример:
print(round(2.675, 2)) # Казалось бы, должно быть 2.68, но получаем 2.67
Почему так происходит? Дело в том, что число 2.675 на самом деле хранится как значение, чуть меньшее, чем 2.675 (примерно 2.67499999999). Когда Python применяет банковское rounding (о котором мы поговорим подробнее дальше), это приводит к округлению в меньшую сторону.
Существует еще одно ограничение: для формата float максимальное число, которое можно представить точно, составляет 2⁵³ (примерно 9 квадриллионов). После этого шаг между соседними представимыми числами увеличивается, что приводит к потере точности.
Все эти особенности делают работу с округлением в Python нетривиальной задачей, требующей понимания принципов представления чисел и выбора правильных инструментов для конкретных задач.
Все способы rounding в Python
Язык Python предлагает несколько подходов, каждый из которых имеет свои особенности и область применения. Рассмотрим их подробно, чтобы вы могли выбрать оптимальный метод для своих задач.
Функция round()
Функция round() — это встроенный инструмент Python для округления чисел, доступный без импорта дополнительных модулей. В общем виде она принимает два параметра: само число и количество знаков после запятой, до которого нужно произвести rounding.
round(number, digits)
Где number — это число, которое требуется округлить, а digits — количество десятичных знаков после запятой (по умолчанию равно 0).
Важное отличие rounding в Python 3 от классических математических правил состоит в том, что здесь применяется «банковское» округление (или rounding до ближайшего чётного). Это означает, что при дробной части, равной точно 0.5, округление происходит до ближайшего чётного числа:
print(round(3.5)) # 4 (ближайшее чётное) print(round(4.5)) # 4 (ближайшее чётное) print(round(5.5)) # 6 (ближайшее чётное)
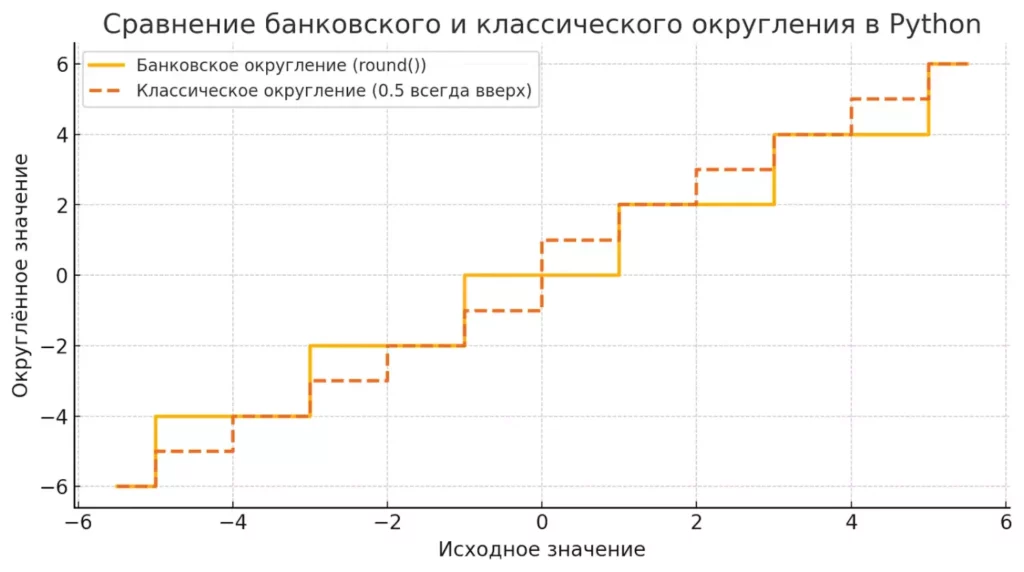
Сравнение банковского округления (round() в Python 3) и классического математического округления (0.5 всегда вверх). При значениях, оканчивающихся на .5, банковское округление ведёт к ближайшему чётному числу, тогда как классическое всегда округляет вверх.
Такой подход позволяет минимизировать систематическую ошибку при статистических вычислениях, так как rounding происходит в обе стороны равновероятно.
Если же мы указываем количество знаков после запятой, то функция round() применяет тот же принцип банковского округления:
print(round(3.145, 2)) # 3.14 print(round(3.155, 2)) # 3.16 (округление до чётного во втором знаке после запятой) print(round(3.145, 1)) # 3.1
Следует отметить, что в некоторых случаях результаты rounding могут быть неожиданными из-за ограничений представления чисел с плавающей запятой:
print(round(2.675, 2)) # 2.67 вместо ожидаемых 2.68
Это происходит потому, что число 2.675 на самом деле хранится как число, чуть меньшее 2.675, и поэтому округляется вниз.
Важно понимать, что функция round() возвращает тип int, если второй параметр не указан или равен нулю, и тип float во всех остальных случаях:
print(type(round(3.14))) # <class 'int'> print(type(round(3.14, 1))) # <class 'float'>
Именно этот метод rounding рекомендуется использовать в большинстве случаев, если нет особых требований к процессу округления.
Приведение к int()
Использование функции int() — это, пожалуй, самый простой способ избавиться от дробной части числа в Python. Однако важно понимать, что это не округление в традиционном понимании, а именно отсечение (усечение) дробной части.
print(int(3.14)) # 3 print(int(3.99)) # 3 (независимо от того, насколько близко к 4)
Как видно из примера, функция int() просто отбрасывает всё, что находится после десятичной точки, не учитывая значение дробной части. Это поведение отличается от математического rounding, где числа округляются к ближайшему целому.
С отрицательными числами функция int() также отбрасывает дробную часть, что даёт результат, отличный от rounding в меньшую сторону:
print(int(-3.14)) # -3 print(int(-3.99)) # -3 (а не -4, как могло бы быть при округлении вниз)
Важно отметить, что int() не является округлением в строгом смысле этого слова — это операция приведения типа (преобразования) из float в int. Она выполняется быстро и не требует импорта дополнительных модулей, что может быть полезно в ситуациях, когда производительность критична.
Если вам действительно нужно rounding по математическим правилам с использованием int(), можно реализовать его вручную, добавляя 0.5 к положительным числам и вычитая 0.5 у отрицательных:
def custom_round(number): if number >= 0: return int(number + 0.5) else: return int(number - 0.5) print(custom_round(3.4)) # 3 print(custom_round(3.5)) # 4 print(custom_round(-3.5)) # -4
Такой подход обеспечивает математическое округление, но требует написания дополнительной функции. В большинстве случаев, если вам нужно настоящее rounding, а не просто отбрасывание дробной части, рекомендуется использовать функцию round() или специализированные функции из модуля math, которые мы рассмотрим далее.
Модуль math: ceil(), floor(), trunc()
Стандартная библиотека Python включает модуль math, который предоставляет ряд математических функций, в том числе и для rounding чисел. В отличие от универсальной функции round(), инструменты из этого модуля позволяют более точно контролировать направление округления.
Для использования этих функций необходимо сначала импортировать модуль:
import math
Рассмотрим три основные функции rounding из этого модуля:
math.ceil() – округление вверх
Функция ceil() (от англ. «ceiling» – потолок) округляет число вверх до ближайшего большего целого, независимо от значения дробной части:
print(math.ceil(3.1)) # 4 print(math.ceil(3.9)) # 4 print(math.ceil(3.0)) # 3
С отрицательными числами она работает по тому же принципу – округляет к ближайшему большему целому:
print(math.ceil(-3.1)) # -3 print(math.ceil(-3.9)) # -3
math.floor() – округление вниз
Функция floor() (от англ. «floor» – пол) округляет число вниз до ближайшего меньшего целого:
print(math.floor(3.1)) # 3 print(math.floor(3.9)) # 3 print(math.floor(3.0)) # 3
С отрицательными числами результат также округляется вниз:
print(math.floor(-3.1)) # -4 print(math.floor(-3.9)) # -4
math.trunc() – усечение дробной части
Функция trunc() (от англ. «truncate» – усекать) просто отбрасывает дробную часть числа, аналогично функции int():
print(math.trunc(3.1)) # 3 print(math.trunc(3.9)) # 3
С отрицательными числами:
print(math.trunc(-3.1)) # -3 print(math.trunc(-3.9)) # -3
Для наглядности представим сравнение функций в виде таблицы:
| Число | math.ceil() | math.floor() | math.trunc() |
|---|---|---|---|
| 3.1 | 4 | 3 | 3 |
| 3.9 | 4 | 3 | 3 |
| -3.1 | -3 | -4 | -3 |
| -3.9 | -3 | -4 | -3 |
Как видно из таблицы, для положительных чисел math.trunc() работает аналогично math.floor(), а для отрицательных – по-разному. Именно это отличие может быть критичным при обработке данных, содержащих отрицательные значения.

Разница между ceil(), floor() и trunc() в Python. Для положительных чисел trunc() работает как floor(), а для отрицательных — ведёт себя иначе, отсекая дробную часть в сторону нуля.
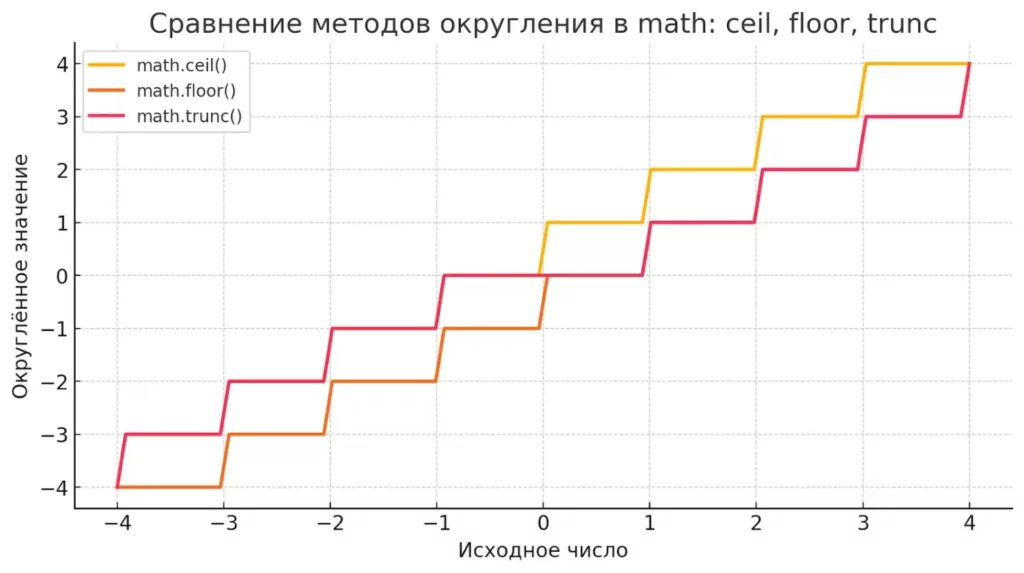
Функции из модуля math особенно полезны, когда требуется гарантированное направление rounding, например:
- В алгоритмах поиска, где нужно определить диапазоны.
- При работе с координатами и графикой.
- В финансовых расчетах, где округление должно происходить в определенную сторону согласно бизнес-правилам.
Используя эти функции, мы можем контролировать поведение нашего кода при работе с дробными числами и избегать нежелательных эффектов, связанных с автоматическим округлением.
Модуль decimal — высокая точность
Когда речь заходит о действительно точных вычислениях, особенно в финансовой сфере, модуль decimal становится незаменимым инструментом в арсенале Python-разработчика. В отличие от типа float, который основан на двоичном представлении и неизбежно приводит к погрешностям, модуль decimal использует десятичную арифметику, которая соответствует тому, как люди выполняют вычисления на бумаге.
Рассмотрим простой пример, демонстрирующий проблему точности с типом float:
print(0.1 + 0.2) # 0.30000000000000004, а не 0.3
Теперь сравним с использованием модуля decimal:
from decimal import Decimal
print(Decimal('0.1') + Decimal('0.2')) # 0.3, как и ожидалось
Обратите внимание на синтаксис: мы передаем строку в конструктор Decimal, а не само число. Это важный момент, поскольку при передаче числа типа float мы уже получим неточное представление:
print(Decimal(0.1)) # 0.1000000000000000055511151231257827021181583404541015625
print(Decimal('0.1')) # 0.1
Округление с помощью quantize()
Для rounding в модуле decimal используется метод quantize(). Этот метод требует указания формата (шаблона), до которого нужно округлить число:
from decimal import Decimal
num = Decimal('3.14159')
rounded = num.quantize(Decimal('1.00')) # Округление до двух знаков после запятой
print(rounded) # 3.14
В данном примере шаблон Decimal(‘1.00’) указывает, что нам нужно два знака после запятой. Важно отметить, что quantize() использует тот же алгоритм «банковского» rounding, что и функция round() по умолчанию.
Однако decimal позволяет гибко настраивать режим rounding с помощью дополнительного параметра rounding. Модуль предоставляет множество констант для различных типов округления:
from decimal import Decimal, ROUND_CEILING, ROUND_FLOOR, ROUND_HALF_UP
num = Decimal('2.675')
# Округление вверх
print(num.quantize(Decimal('0.01'), rounding=ROUND_CEILING)) # 2.68
# Округление вниз
print(num.quantize(Decimal('0.01'), rounding=ROUND_FLOOR)) # 2.67
# Классическое математическое округление
print(num.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)) # 2.68
Вот некоторые из доступных режимов rounding:
- ROUND_CEILING — всегда округляет в сторону положительной бесконечности.
- ROUND_FLOOR — всегда округляет в сторону отрицательной бесконечности.
- ROUND_HALF_UP — классическое математическое округление (0.5 округляется вверх).
- ROUND_HALF_DOWN — округление, при котором 0.5 округляется вниз.
- ROUND_HALF_EVEN — банковское округление (по умолчанию).
- ROUND_05UP — округляет от нуля, если последняя цифра 0 или 5.
Сравнение с round()
Сравним поведение decimal и встроенной функции round() на примере, который мы упоминали ранее:
print(round(2.675, 2)) # 2.67 (из-за неточного представления float)
from decimal import Decimal, ROUND_HALF_UP
print(Decimal('2.675').quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)) # 2.68
Как видим, decimal дает более предсказуемый результат, соответствующий математическим правилам rounding.
Модуль decimal также позволяет контролировать другие аспекты вычислений, такие как количество значащих цифр, обработка деления на ноль и т.д. через контекст decimal.getcontext().
Несмотря на большую точность, использование decimal имеет и свои недостатки: вычисления выполняются медленнее, чем с типом float, и требуется больше памяти. Поэтому этот модуль рекомендуется применять там, где точность критически важна — в финансовых вычислениях, при работе с валютами или в научных расчётах, требующих высокой точности.
Форматирование строк для округления вывода
Иногда нужно не изменить само число, а просто красиво вывести его на экран, например, в отчётах, интерфейсах или логах. В таких случаях удобно использовать форматирование строк.
Это не округление в строгом смысле — значение остаётся прежним, меняется только его отображение. Но для вывода пользователю этого достаточно.
Способы форматирования:
f-строки (Python 3.6+)
x = 3.14159
print(f"{x:.2f}") # 3.14
Функция format()
x = 3.14159 print(format(x, ".2f")) # 3.14
Оператор % (старый стиль)
x = 3.14159
print("%.2f" % x) # 3.14
Когда использовать?
- Для вывода чисел в удобном виде (например, 2 знака после запятой).
- При подготовке отчётов, отображении цен, процентов, показателей на графиках.
- Когда важно оставить внутреннее значение без изменений, но показать его в округлённой форме.
Важно помнить:
- Это не влияет на вычисления! Оригинальное число сохраняет все знаки после запятой.
- Если нужно изменить именно значение, используйте round(), decimal, math.ceil() и другие методы.
Какой метод выбрать в зависимости от задачи
Выбор оптимального метода rounding в Python зависит от конкретной задачи, требований к точности и характера данных. Проанализируем различные подходы и определим, когда какой инструмент будет наиболее уместен.
Сравнительная таблица методов округления
| Метод | Преимущества | Недостатки | Когда использовать |
|---|---|---|---|
| round() | Встроенная функция (не требует импорта)
Банковское rounding предотвращает смещение Простой синтаксис |
Непредсказуемость с числами, оканчивающимися на .5
Проблемы с точностью при работе с float |
Общие случаи rounding
Когда важно избежать накопления погрешности |
| int() | Максимальная скорость
Простейший синтаксис Предсказуемое поведение |
Не является округлением, а отсечением
Может давать неожиданные результаты при неправильном использовании |
Когда нужна только целая часть
В высоконагруженных приложениях Когда rounding не требуется |
| math.ceil() | Гарантированное rounding вверх
Работает предсказуемо с отрицательными числами |
Требует импорта модуля math
Может создавать смещение при статистических расчетах |
Расчет необходимых ресурсов
Определение верхних границ Вычисление максимальных значений |
| math.floor() | Гарантированное округление вниз
Предсказуемое поведение |
Требует импорта модуля math
Может создавать смещение |
Определение нижних границ
Отбрасывание избыточных данных Консервативные оценки |
| math.trunc() | • Просто отбрасывает дробную часть
• Предсказуемое поведение |
Отличается от rounding
Требует импорта модуля math |
Когда требуется только целая часть
Вместо `int()` для единообразия с другими функциями math |
| decimal.Decimal.quantize() | Высокая точность
Контроль над режимом округления Предсказуемость с десятичными дробями |
Более медленная работа
Больше строк кода Требуется импорт |
Финансовые расчеты
Работа с валютами Научные вычисления Когда точность критична |
Практические кейсы
Кейс 1: Финансовые расчеты
В финансовой сфере точность и предсказуемость rounding имеют критическое значение. Даже небольшие погрешности могут привести к существенным расхождениям в итоговых суммах, особенно при работе с большими объемами транзакций.
from decimal import Decimal, ROUND_HALF_UP, ROUND_DOWN
def calculate_interest(principal, rate, years):
"""Расчет процентов по вкладу с использованием Decimal для точности"""
principal = Decimal(str(principal))
rate = Decimal(str(rate))
# Рассчитываем итоговую сумму
amount = principal * (1 + rate) ** years
# Округляем до копеек согласно банковским правилам
return amount.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)
# Для налоговых расчетов может требоваться округление вниз
def calculate_tax(income):
"""Расчет налога с округлением вниз до целых рублей"""
income = Decimal(str(income))
tax_rate = Decimal('0.13') # 13%
tax_amount = income * tax_rate
return tax_amount.quantize(Decimal('1.'), rounding=ROUND_DOWN)
print(calculate_interest(10000, 0.05, 5)) # 12762.82
print(calculate_tax(50000)) # 6500
Для финансовых расчетов всегда рекомендуется использовать decimal с явным указанием режима rounding, соответствующего бизнес-требованиям.
Кейс 2: Обработка данных и статистика
При обработке научных или аналитических данных часто требуется балансировать между точностью и производительностью. Здесь выбор метода округления зависит от конкретного этапа анализа:
import math
import numpy as np
from decimal import Decimal
def process_measurement_data(measurements):
"""Обработка экспериментальных данных с разными типами округления"""
# Округляем вверх для расчета необходимого объема выборки
sample_size_needed = math.ceil(len(measurements) * 0.15)
# Используем встроенный round для расчета средних значений
average = round(sum(measurements) / len(measurements), 2)
# Для точного статистического анализа используем numpy
median = np.median(measurements)
# Для итоговых финансовых показателей используем Decimal
total_cost = sum(Decimal(str(m)) * Decimal('1.05') for m in measurements)
total_cost = total_cost.quantize(Decimal('0.01'))
return {
'sample_size': sample_size_needed,
'average': average,
'median': median,
'total_cost': total_cost
}
При работе с научными данными выбор метода rounding должен учитывать специфику области и потенциальное влияние округления на итоговые результаты исследования.
В обоих примерах мы видим, что оптимальный выбор метода rounding зависит от контекста использования, требований к точности и особенностей данных. Уделите этому выбору должное внимание — это поможет избежать многих проблем в будущем.
Частые ошибки и как их избежать
При работе с округлением в Python разработчики часто допускают ряд типичных ошибок, которые могут привести к неожиданным результатам и сложно диагностируемым багам. Рассмотрим наиболее распространенные проблемы и способы их предотвращения.
Округление отрицательных чисел
Одна из самых частых ошибок — неверное понимание того, как работает округление с отрицательными числами:
# Использование int() вместо math.floor() print(int(-3.7)) # Даст -3, а не -4 print(math.floor(-3.7)) # Правильно: -4
При работе с отрицательными числами следует четко различать усечение дробной части (int() или math.trunc()) и математическое округление вниз (math.floor()).
Ошибки с банковским округлением
Многие разработчики ожидают, что функция round() работает по классическим математическим правилам, и удивляются при получении неожиданных результатов:
print(round(2.5)) # 2, а не 3 print(round(3.5)) # 4
Вместо того чтобы полагаться на интуитивное понимание округления, необходимо помнить о банковском методе, используемом в Python 3, и при необходимости реализовать классическое математическое округление:
def math_round(x):
"""Классическое математическое округление (0.5 всегда вверх)"""
from decimal import Decimal, ROUND_HALF_UP
return int(Decimal(str(x)).quantize(Decimal('1'), rounding=ROUND_HALF_UP))
print(math_round(2.5)) # 3
print(math_round(3.5)) # 4
Проблемы с точностью float
Невнимание к особенностям представления чисел с плавающей запятой приводит к загадочным ошибкам округления:
print(round(2.675, 2)) # 2.67 вместо ожидаемых 2.68
Для избежания таких проблем при работе с критически важными расчетами следует использовать decimal:
from decimal import Decimal, ROUND_HALF_UP
print(Decimal('2.675').quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)) # 2.68
Ошибочное представление о int()
Многие новички воспринимают int() как функцию округления, что может привести к логическим ошибкам:
values = [3.2, 3.5, 3.7, 3.9] # Неправильно, просто отсекает дробную часть rounded = [int(v) for v in values] # [3, 3, 3, 3] # Правильно, математическое округление rounded = [round(v) for v in values] # [3, 4, 4, 4]
Проблемы с накоплением ошибок
При многократном применении округления в циклических вычислениях может происходить накопление ошибок:
# Неправильно: округление на каждой итерации result = 0 for i in range(1000): result += round(0.1, 1) print(result) # 100.0 # Правильно: округление только финального результата result = 0 for i in range(1000): result += 0.1 print(round(result, 1)) # 100.0
Для предотвращения подобных проблем следует откладывать округление до последнего момента, когда это возможно, особенно в циклических вычислениях.
Знание этих типичных ошибок и понимание внутренних механизмов округления в Python поможет вам писать более надежный и предсказуемый код, избегая неприятных сюрпризов при работе с числовыми данными.
Заключение
Подводя итоги нашего глубокого погружения в мир округления чисел в Python, мы можем сформулировать несколько ключевых выводов, которые помогут вам принимать обоснованные решения при работе с числовыми данными.
Округление — это не просто математическая операция, а важный инструмент, который требует осознанного подхода в зависимости от контекста задачи. Python предоставляет богатый набор методов для различных сценариев, каждый со своими особенностями и областью применения.
Основные принципы, которые следует помнить:
- Округление в Python связано с особенностями представления чисел с плавающей запятой. Даже простые операции, вроде сложения 0.1 + 0.2, могут давать неожиданные результаты из-за формата IEEE 754.
- Функция
round()в Python использует банковское округление, а не классическое. Числа, заканчивающиеся на .5, округляются к ближайшему чётному, чтобы минимизировать систематическую ошибку. - Использование
int()иmath.trunc()— это не округление, а усечение дробной части. Эти функции просто отбрасывают дробную часть, что может привести к логическим ошибкам, особенно с отрицательными числами. - Модуль
mathпредоставляет точечные методы для управления направлением округления.math.ceil()всегда округляет вверх, аmath.floor()— вниз, что полезно при расчётах границ или допусков. - Модуль
decimalпозволяет выполнять точные десятичные вычисления без ошибок float-арифметики. Это лучший выбор для финансовых операций, потому чтоdecimalточно работает с дробными числами и позволяет выбирать режим округления. - Форматирование строк (
f-строки,format(),%) используется для округления при выводе, а не при вычислениях. Это удобно для отображения чисел в нужном формате, но не изменяет сами значения. - Неправильный выбор метода округления может привести к накоплению ошибок в циклах и больших вычислениях. Лучше откладывать округление до финального этапа расчётов, чтобы избежать накапливающихся отклонений.
- Для разных задач нужны разные методы округления. Финансовые расчёты, статистика, визуализация данных, игры или научные вычисления требуют своего подхода.
- Частые ошибки связаны с недопониманием различий между усечением, округлением вверх, вниз и банковским округлением. Это приводит к багам, особенно при работе с отрицательными числами и числами, оканчивающимися на .5.
Хотите прокачать Python для реальных задач? Загляните на подборку курсов по Python-разработке.
Рекомендуем посмотреть курсы по Python
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Профессия Python-разработчик
|
Eduson Academy
76 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
6 месяцев
|
Старт
7 декабря
|
Ссылка на курс |
|
Курс Go-разработчик (Junior)
|
Level UP
36 отзывов
|
Цена
45 500 ₽
|
От
11 375 ₽/мес
|
Длительность
3 месяца
|
Старт
27 января
|
Ссылка на курс |
|
Fullstack-разработчик на Python
|
Нетология
44 отзыва
|
Цена
с промокодом kursy-online
146 500 ₽
308 367 ₽
|
От
4 282 ₽/мес
|
Длительность
18 месяцев
|
Старт
18 декабря
|
Ссылка на курс |
|
Python-разработчик
|
Академия Синергия
32 отзыва
|
Цена
91 560 ₽
228 900 ₽
|
От
3 179 ₽/мес
4 552 ₽/мес
|
Длительность
6 месяцев
|
Старт
9 декабря
|
Ссылка на курс |
|
Профессия Python-разработчик
|
Skillbox
191 отзыв
|
Цена
Ещё -20% по промокоду
70 960 ₽
141 919 ₽
|
От
5 913 ₽/мес
9 715 ₽/мес
|
Длительность
11.1 месяцев
|
Старт
9 декабря
|
Ссылка на курс |

Как дизайнеру развивать насмотренность
Как развить насмотренность, чтобы идеи не заканчивались, а стиль стал узнаваемым? Рассказываем, какие привычки, ресурсы и подходы реально работают.

Нужна ли вам проприетарная лицензия? Разбираем по полочкам
Проприетарные лицензии — это не просто «закрытый код». Мы объясним, почему такие модели всё ещё актуальны, где они выигрывают у open source и когда они действительно нужны вашему проекту.
Факторы ранжирования сайта: что влияет на позиции в поиске
Факторы ранжирования сайта — не магия, а набор конкретных параметров, которые можно оптимизировать. В этой статье — полный разбор.

Character AI — что это и как пользоваться
Character AI — это нейросеть, которая способна не просто отвечать, а имитировать поведение, стиль речи и даже эмоции реальных и вымышленных персонажей. Хотите поболтать с Сократом или с куском сыра? Здесь это возможно.