Как применять закон Литтла в рабочих процессах: расчёты, примеры, ошибки и ограничения
Закон Литтла — один из тех редких случаев, когда математическая формула из теории массового обслуживания оказывается применима практически к любой системе, где есть поток работы. Открытый профессором Джоном Литтлом из MIT в 1954 году и формально доказанный им же в 1961-м, этот закон первоначально описывал поведение очередей: от клиентов в банке до автомобилей на заправке. Однако его универсальность быстро вышла за пределы теории очередей и нашла применение в самых разных областях — от логистики до управления программными проектами.

В чём суть? Закон Литтла устанавливает строгую математическую взаимосвязь между тремя ключевыми характеристиками любой системы: количеством элементов в процессе, скоростью их прохождения и временем, которое каждый элемент проводит в системе. Звучит абстрактно, но давайте разберём это на двух уровнях:
Простое определение: Закон Литтла показывает, что среднее количество задач в работе равно произведению скорости их выполнения на среднее время, которое требуется на один таск. Иными словами, чем больше задач вы берёте одновременно и чем дольше они выполняются, тем выше нагрузка на систему.
Формальное определение: В стабильной системе среднее количество элементов (L) равно произведению средней скорости поступления элементов (λ) на среднее время пребывания элемента в системе (W). Формула: L = λ × W.
Почему закон работает для систем разного типа? Потому что он не зависит от конкретной природы «элементов» — будь то клиенты в очереди, детали на конвейере или задачи в Kanban-доске. Закон Литтла описывает фундаментальное свойство потока: если система стабильна (то есть в неё поступает примерно столько же, сколько из неё выходит), то взаимосвязь этих трёх параметров остаётся неизменной. Это делает его мощным инструментом для анализа и оптимизации рабочих процессов — от производства до разработки ПО.
- Базовая формула закона Литтла L = λ × W и её расшифровка
- Как закон Литтла работает в управлении задачами и Kanban
- Как рассчитать оптимальный WIP-лимит по закону Литтла
- Как применять закон Литтла в реальных командах
- Мифы и заблуждения о законе Литтла
- Как внедрить WIP-лимиты и улучшить процессы
- Заключение
- Рекомендуем посмотреть курсы по управлению проектами
Базовая формула закона Литтла L = λ × W и её расшифровка
Формула закона Литтла выглядит обманчиво просто: L = λ × W. Три переменных, одно умножение — и перед нами инструмент, способный описать поведение сложных систем. Однако за этой простотой скрывается глубокая взаимосвязь метрик, которую важно понимать для эффективного управления потоком работы.
Давайте разберём каждый параметр:
- L (Work in Progress, WIP) — среднее количество элементов, находящихся в системе в данный момент времени. В контексте управления задачами это количество тасков, которые команда ведёт одновременно: от момента начала работы до момента завершения. Например, если на вашей Kanban-доске в колонках «В работе», «Тестирование» и «Проверка» висит 8 задач — это и есть ваш текущий WIP.
- λ (Throughput, пропускная способность) — средняя скорость, с которой элементы проходят через систему и завершаются. Измеряется в единицах за период времени: задач в день, заказов в неделю, релизов в месяц. Если ваша команда закрывает в среднем 2 таска в день, то λ = 2 задачи/день.
- W (Cycle Time или Lead Time, время цикла) — среднее время, которое один элемент проводит в системе от начала до завершения. В разработке это может быть время от момента, когда разработчик взял таск в работу, до момента его полного завершения. Например, если задача в среднем проходит путь от «взято в работу» до «готово» за 4 дня, то W = 4 дня.
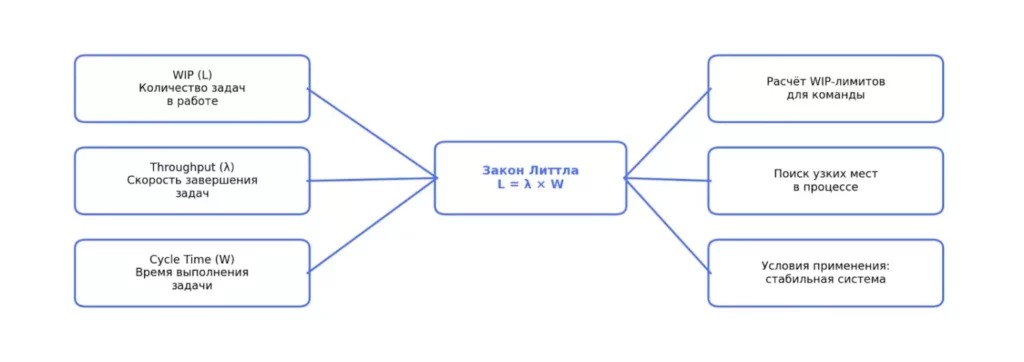
Майнд-карта показывает ключевые элементы закона Литтла и связи между ними. В центре — формула L = λ × W, слева — базовые метрики процесса, справа — основные области применения в работе команд. Такая схема помогает быстро увидеть картину целиком и понять, как формула используется на практике.
Визуальная интерпретация формулы проста: если вы знаете любые два параметра, третий вычисляется автоматически. Закрываете 2 задачи в день, и каждая занимает 4 дня? Значит, в системе постоянно находится L = 2 × 4 = 8 тасков. Хотите сократить время выполнения до 2 дней при том же throughput? Придётся снизить WIP до 4 задач.
Как закон Литтла работает в управлении задачами и Kanban
Чтобы понять, как абстрактная математическая формула применяется к реальной работе команды, давайте вернёмся к классическому примеру из теории очередей — но адаптируем его под современные реалии.
Представьте популярный фуд-трейлер, где продают буррито с органическими грибами шиитаке. Каждый час приходит 20 клиентов (λ = 20 клиентов/час), каждый задерживается на полчаса, чтобы поесть и поболтать (W = 0,5 часа). Сколько клиентов одновременно находится у трейлера? L = 20 × 0,5 = 10 клиентов.
Теперь перенесём эту логику на рабочий процесс команды:
- Клиенты, приходящие каждый час → таски, поступающие в работу (из бэклога в колонку «В работе»).
- Время, которое клиент проводит у трейлера → время цикла таска (от взятия в работу до завершения).
- Количество клиентов у трейлера → количество задач в процессе (WIP).
- Скорость обслуживания клиентов → пропускная способность команды (throughput).
Допустим, ваша команда берёт в работу 1,5 таска в день, и каждыйв среднем выполняется за 4 дня. Тогда в любой момент времени в работе находится L = 1,5 × 4 = 6 задач. Это не значит, что ровно 6 всегда висят на доске — речь идёт о среднем значении за длительный период.
Аналогия работает в обе стороны: если вы видите, что на доске постоянно 12 тасков, а throughput составляет 2 задачи в день, то среднее время цикла W = 12 / 2 = 6 дней. Формула превращается в диагностический инструмент.
Практическая модель: как выглядит поток задач на доске Kanban
Давайте рассмотрим типичную Kanban-доску с колонками: «В работе» → «Тестирование» → «Проверка» → «Готово». Каждая колонка представляет собой этап процесса, и задачи движутся слева направо по мере выполнения.
Что происходит, когда WIP слишком высок? Представьте ситуацию: на доске висит 10 дел, распределённых по всем этапам. Разработчики переключаются между ними, тестировщики не успевают проверять, код-ревью затягивается. В результате ни одна задача не движется дальше — все застряли в процессе. Формально WIP = 10, но throughput стремится к нулю, а cycle time растёт до бесконечности.
Пример из практики: команда установила WIP-лимит в 6 тасков для всей доски. Как только шесть оказываются в процессе, новые задачи не берутся в работу, пока хотя бы одна не будет завершена. Это создаёт здоровое давление: если таск застрял в колонке «Проверка», вся команда заинтересована помочь его завершить, иначе новая работа не начнётся.
Закон Литтла здесь работает как барометр: если при фиксированном WIP вдруг начинает расти cycle time, это сигнал о проблемах в процессе. Возможно, один из этапов стал узким местом, или команда взяла слишком сложные задачи. Формула не даст ответов, но укажет направление для анализа.
Как рассчитать оптимальный WIP-лимит по закону Литтла
Пошаговый алгоритм расчёта
Теоретическая формула хороша, но как применить её на практике? Давайте разберём пошаговый процесс расчёта оптимального WIP-лимита для вашей команды.
Шаг 1. Соберите исторические данные. Вам понадобятся данные минимум за 2–4 недели стабильной работы. Ключевые показатели: сколько дел команда завершила (для расчёта throughput) и сколько времени в среднем занимало выполнение одной задачи (cycle time). Эти данные можно извлечь из систем управления — Jira, Kaiten, Trello или любой другой системы с учётом времени.
Пример таск-трекера (Kaiten). На скриншоте видны столбцы с задачами – “в работе” и готово”. Источник: официальный сайт.
Шаг 2. Рассчитайте средний throughput (λ). Разделите общее количество завершённых тасков на количество рабочих дней в периоде наблюдения. Например, за 20 рабочих дней команда закрыла 30 тасков: λ = 30 / 20 = 1,5 задачи в день.
Шаг 3. Определите средний cycle time (W). Для каждой завершённой посчитайте время от момента начала работы до окончания, затем найдите среднее значение. Допустим, среднее время составило 4 дня: W = 4 дня.
Шаг 4. Подставьте данные в формулу.
L = λ × W = 1,5 × 4 = 6 задач.
Это и есть расчётный оптимальный WIP-лимит для вашей команды.
Шаг 5. Проверьте результат на практике. Установите WIP-лимит на уровне 6 тасков и наблюдайте за системой 1–2 недели. Если задачи начали двигаться быстрее, а cycle time сократился — лимит работает. Если команда простаивает (throughput упал) — возможно, лимит слишком жёсткий и его нужно немного увеличить.
| Параметр | Как получить | Пример значения |
|---|---|---|
| Throughput (λ) | Завершённые задачи / рабочие дни | 1,5 таска/день |
| Cycle Time (W) | Среднее время выполнения | 4 дня |
| WIP-лимит (L) | λ × W | 6 задач |
Важно понимать: закон Литтла даёт отправную точку, а не абсолютную истину. Полученное число — это базовый ориентир, который нужно адаптировать под реальность вашей команды.
Пример расчёта WIP-лимита
Рассмотрим конкретный кейс. Команда разработки анализирует свои показатели за последний месяц:
- Throughput (λ): команда завершает в среднем 1,5 задачи в день (за 20 рабочих дней закрыли 30).
- Cycle Time (W): среднее время от взятия таска в работу до его завершения составляет 4 дня.
Подставляем в формулу: L = 1,5 × 4 = 6 задач.
Что это значит? В идеальной стабильной системе на доске команды должно находиться около 6 тасков одновременно. Это число учитывает скорость работы команды и время, необходимое для прохождения задачи через все этапы процесса.
Почему это отправная точка, а не догма? Потому что закон Литтла оперирует средними величинами и предполагает стабильность системы. В реальности же:
- Задачи могут сильно различаться по сложности (одна за час, другая — за неделю).
- Состав команды может меняться (отпуска, больничные, новые сотрудники).
- Внешние факторы влияют на процесс (срочные правки, технические проблемы, изменения приоритетов).
Поэтому полученное число 6 — это гипотеза, которую нужно протестировать. Установите WIP-лимит на этом уровне, понаблюдайте за метриками и корректируйте при необходимости. Возможно, команде комфортнее работать с лимитом в 5 задач (более строгий фокус) или в 7 (больше гибкости). Главное — не уходить далеко от расчётного значения без веских причин.
Как применять закон Литтла в реальных командах
Когда система считается «стабильной»
Закон Литтла работает безупречно — но только в стабильных системах. Что это значит на практике? Стабильность подразумевает, что система находится в состоянии динамического равновесия: количество тасков, поступающих в работу, примерно равно количеству завершаемых задач за тот же период времени.
- Условие равенства input ≈ output. Если за неделю команда берёт в работу 10 тасков и завершает 10, система стабильна. Если же каждую неделю в работу поступает 15 задач, а завершается только 10, WIP будет неуклонно расти, а система — выходить из равновесия. В таких условиях формула закона Литтла теряет предсказательную силу.
- Корректность исторических данных. Для применения закона нужны качественные данные за достаточно длительный период — минимум 2–4 недели, в идеале 1–2 месяца. Данные должны отражать типичную работу команды, а не исключительные периоды (например, предрелизный крунч или новогодние праздники). Чем регулярнее поток задач и чем стабильнее процесс, тем точнее будут расчёты.
- Влияние изменений в составе команды и процессах. Если в команду пришёл новый разработчик, throughput временно снизится (пока человек вливается в процесс). Если команда внедрила автоматизированное тестирование, cycle time может сократиться. Любые значительные изменения требуют пересмотра расчётов — старые данные больше не отражают реальность системы.
Когда закон Литтла НЕ работает
Несмотря на универсальность, закон Литтла имеет чёткие границы применимости. Важно понимать, когда формула перестаёт быть полезной, чтобы не принимать ошибочных решений на основе некорректных расчётов.
- Нестабильность потока. Если таски поступают хаотично (сегодня 2, завтра 20), а команда постоянно переключается между проектами, стабильности нет. Средние значения в таких условиях становятся бессмысленными — они скрывают реальную картину за цифрами, которые ничего не объясняют.
- Попытки использовать закон для прогнозов по конкретным задачам. Закон Литтла описывает поведение системы в среднем, но не предсказывает судьбу отдельного таска. Если средний cycle time составляет 4 дня, это не значит, что конкретная задача будет выполнена ровно за 4 дня. Одна может занять 2 дня, другая — 8. Для точных прогнозов по отдельным задачам нужны другие инструменты — например, анализ распределения cycle time с использованием процентилей.
- Перегруженная система с неконтролируемым WIP. Если на доске висит 30 дел, а в команде 5 человек, система находится в состоянии перегрузки. В таких условиях throughput стремится к нулю (ничего не завершается), а cycle time растёт экспоненциально. Формула технически работает (L = λ × W), но становится бесполезной для управления — сначала нужно вернуть систему в стабильное состояние, резко сократив WIP.
- Отсутствие исторических данных. Новая команда, новый проект, новый процесс — если данных меньше чем за 2 недели работы, применять закон Литтла преждевременно. Лучше начать с консервативных оценок и постепенно накапливать статистику.
Закон Литтла — это не магический инструмент, который исправит плохо организованный процесс. Это диагностический инструмент, который работает в руках тех, кто уже навёл базовый порядок в своей системе управления задачами.
Как выявлять «узкие места» с помощью закона Литтла
Одно из самых ценных применений закона Литтла — диагностика проблем в процессе. Формула не скажет вам, где именно проблема, но укажет, что что-то идёт не так.
Рост cycle time — возможные причины:
- Одна из колонок на доске стала узким местом (например, таски скапливаются в «Code Review», потому что ревьюеров не хватает).
- Увеличилась сложность задач, но WIP-лимит остался прежним — команда не справляется с нагрузкой.
- Появились внешние зависимости, которые тормозят процесс (ожидание ответа от заказчика, интеграция с другой системой).
Замедление throughput — где искать проблемы:
- Команда взяла слишком много задач одновременно, и фокус размылся — в итоге ничего не доводится до конца.
- Изменился состав команды (кто-то ушёл в отпуск или уволился), и нагрузка перераспределилась неравномерно.
- Процесс перегружен бюрократией: слишком много согласований, встреч, проверок.
Пример анализа колонки «Тестирование».
Допустим, вы заметили, что среднее время цикла выросло с 4 до 6 дней. Посмотрите на доску: где таски проводят больше всего времени? Если в колонке «Тестирование» постоянно висит 4–5 штук, а тестировщик один — вот ваше узкое место. Решение: либо добавить ресурсы (нанять тестировщика), либо автоматизировать часть проверок, либо установить WIP-лимит на колонку «Тестирование» (например, не больше 2 задач одновременно), чтобы разработчики не закидывали туда всё подряд.

Схема Kanban-доски показывает типичное узкое место процесса: задачи скапливаются на этапе тестирования. При этом общее количество задач в работе остаётся высоким, а завершение замедляется. Рост cycle time в такой ситуации — прямой сигнал о проблеме в конкретном этапе процесса.
Мифы и заблуждения о законе Литтла
Закон Литтла окружён множеством заблуждений, которые возникают из-за попыток применить его там, где он не работает, или интерпретировать результаты слишком буквально. Давайте разберём наиболее распространённые мифы и выясним, как всё обстоит на самом деле.
- Миф 1: Закон Литтла даёт точные обещания по срокам конкретных задач. Как на самом деле: Закон оперирует средними величинами и описывает поведение системы в целом, а не отдельных элементов. Если средний cycle time составляет 4 дня, это не гарантирует, что следующая задача будет выполнена ровно за 4 дня. Одна может занять 2 дня, другая — 8. Для прогнозирования конкретных сроков нужны дополнительные инструменты: анализ распределения данных, процентили (например, 85-й процентиль cycle time), учёт сложности тасков.
- Миф 2: Увеличение WIP автоматически увеличивает throughput. Как на самом деле: Формула L = λ × W не означает, что рост WIP приведёт к росту пропускной способности. На практике чаще происходит обратное: увеличение количества задач в работе приводит к частым переключениям контекста, снижению концентрации и, как следствие, к росту cycle time при неизменном (или даже падающем) throughput. Закон Литтла лишь фиксирует взаимосвязь этих параметров, но не диктует причинно-следственные связи.
- Миф 3: Закон Литтла работает для любой отдельной задачи. Как на самом деле: Закон описывает среднее поведение системы за длительный период, а не судьбу конкретного элемента. Попытка использовать формулу для расчёта времени выполнения одного таска — фундаментальная ошибка. Вариативность в реальных процессах слишком велика: задачи различаются по сложности, могут блокироваться внешними зависимостями, попадать на выходные или праздники. Средние величины полезны для планирования в целом, но не для точечных прогнозов.
- Миф 4: Закон Литтла применим к хаотичным системам. Как на самом деле: Формула работает только в стабильных системах, где поток тасков относительно равномерен, а процесс предсказуем. Если сегодня команда работает над проектом A, завтра переключается на срочную задачу из проекта B, а послезавтра возвращается к A — стабильности нет. В хаотичных системах средние значения теряют смысл, потому что они не отражают реальное состояние процесса. Сначала нужно навести порядок, а потом применять аналитические инструменты.
Понимание этих ограничений критически важно. Закон Литтла — мощный, но специализированный инструмент. Он не заменяет здравый смысл, опыт команды и качественный анализ процессов. Его задача — сделать видимыми закономерности, которые иначе остались бы скрытыми за потоком ежедневной работы.
Команда обсуждает рабочий процесс и анализирует движение задач по этапам. Участники фокусируются на количестве задач в работе и скорости их завершения, а не на отдельных тасках. Такая визуализация хорошо передаёт идею применения закона Литтла в повседневной командной работе.
Как внедрить WIP-лимиты и улучшить процессы
Понимание закона Литтла — это одно, а внедрение WIP-лимитов в реальную работу команды — совсем другое. Теория должна превратиться в практические шаги, которые изменят способ работы команды. Давайте разберём, как это сделать системно и без лишних потрясений.
- Шаг 1. Установите WIP-лимиты на основе расчётов. Используйте формулу L = λ × W, чтобы получить базовое значение. Допустим, вы рассчитали, что оптимальный WIP составляет 6 тасков для всей команды. Теперь распределите этот лимит по этапам процесса. Например: «В работе» — максимум 3, «Тестирование» — максимум 2, «Code Review» — максимум 1 задача. Распределение зависит от того, где обычно возникают узкие места.
- Шаг 2. Визуализируйте лимиты на доске. Сделайте WIP-лимиты видимыми для всей команды. На физической Kanban-доске можно написать цифры над колонками (например, «Тестирование [2]»). В электронных системах (Jira, Kaiten, Trello) настройте автоматические предупреждения или блокировку при превышении лимита. Главное — чтобы каждый член команды в любой момент понимал, есть ли возможность взять новую задачу или нужно сначала завершить текущую работу.
- Шаг 3. Протестируйте лимиты в течение 1–2 недель. Первые дни будут непривычными. Команда может чувствовать дискомфорт: «Почему я не могу взять новый таск, если у меня есть время?» Объясните логику: цель — не ограничить продуктивность, а повысить фокус и ускорить прохождение задач через систему. Наблюдайте за метриками: изменился ли cycle time? Вырос или упал throughput? Как чувствует себя команда?
- Шаг 4. Адаптируйте лимиты под реальную команду. После тестового периода соберите обратную связь. Возможно, лимит слишком жёсткий, и люди простаивают в ожидании, пока таск пройдёт review. Или, наоборот, лимит слишком мягкий, и на доске по-прежнему висит слишком много задач. Корректируйте постепенно: увеличьте или уменьшите лимит на 1–2 штуки и снова наблюдайте за результатами.
- Шаг 5. Анализируйте результаты эксперимента. Через месяц работы с WIP-лимитами сравните данные с периодом «до внедрения». Ключевые вопросы: сократилось ли среднее время цикла? Стала ли команда завершать больше тасков за спринт? Уменьшилось ли количество переключений между задачами? Чувствуют ли сотрудники, что работа стала более предсказуемой? Если ответы положительные — лимиты работают. Если нет — ищите причины и корректируйте подход.
Важный момент: WIP-лимиты — это не жёсткое правило, высеченное в камне. Это инструмент, который команда использует для самоорганизации. Если возникла критическая ситуация (production down, срочный баг), лимит можно временно нарушить — но с пониманием, что это исключение, а не норма. После разрешения кризиса команда возвращается к установленным правилам.
Заключение
Закон Литтла — это не просто математическая формула из учебника по теории массового обслуживания. Это практический инструмент, который меняет способ работы команды и делает процессы более осознанными и управляемыми. Давайте подведём итоги и выделим ключевые преимущества, которые получает команда от его применения:
- Закон Литтла описывает связь между WIP, throughput и временем цикла. Он позволяет понять, как количество задач в работе влияет на скорость и предсказуемость процессов.
- Формула L = λ × W применима только к стабильным системам. Для корректных расчётов важно, чтобы входящий и исходящий поток задач были сбалансированы.
- Закон помогает рассчитывать WIP-лимиты. Используя исторические данные, команда получает обоснованную отправную точку для настройки ограничений.
- Рост WIP почти всегда ведёт к увеличению cycle time. Попытки брать больше задач одновременно обычно замедляют выполнение, а не ускоряют его.
- Закон Литтла — диагностический инструмент. Он не даёт точных прогнозов по отдельным задачам, но помогает выявлять узкие места и проблемы в процессе.
Если вы только начинаете осваивать управление проектами и процессами, рекомендуем обратить внимание на подборку курсов по проджект-менеджменту. В таких программах обычно сочетаются теоретическая база и практические задания, которые помогают применять закон Литтла в реальных командах.
Рекомендуем посмотреть курсы по управлению проектами
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Менеджер проектов
|
Eduson Academy
109 отзывов
|
Цена
119 600 ₽
|
От
119 600 ₽/мес
Беспроцентная. На 1 год.
|
Длительность
3 месяца
|
Старт
22 февраля
|
Подробнее |
|
Project manager
|
Нетология
46 отзывов
|
Цена
107 300 ₽
238 536 ₽
с промокодом kursy-online
|
От
3 313 ₽/мес
Без переплат на 2 года.
|
Длительность
10 месяцев
|
Старт
25 февраля
|
Подробнее |
|
Менеджер проектов
|
Академия Синергия
36 отзывов
|
Цена
90 636 ₽
|
От
3 777 ₽/мес
0% на 24 месяца
|
Длительность
6 месяцев
|
Старт
3 марта
|
Подробнее |
|
Профессия Менеджер проектов
|
Skillbox
225 отзывов
|
Цена
105 750 ₽
211 499 ₽
Ещё -20% по промокоду
|
От
3 411 ₽/мес
Без переплат на 31 месяц с отсрочкой платежа 6 месяцев.
9 572 ₽/мес
|
Длительность
12 месяцев
|
Старт
23 февраля
|
Подробнее |
|
Менеджер проектов
|
Яндекс Практикум
98 отзывов
|
Цена
165 500 ₽
|
От
19 000 ₽/мес
На 2 года.
|
Длительность
6 месяцев
Можно взять академический отпуск
|
Старт
26 февраля
|
Подробнее |

PERT-диаграмма: инструмент, который делает проект предсказуемым
Как избежать срывов сроков и не потеряться в сложных задачах? PERT-диаграмма помогает визуализировать ключевые этапы проекта, оптимизировать время и управлять рисками.

Performance review: что это, как провести и зачем нужно
Что такое performance review и почему его внедряют лучшие компании мира? Расскажем, как построить процесс так, чтобы он помогал развивать людей, а не превращался в бюрократию.

Как избежать SQL-инъекций в PHP? Практические советы и примеры
SQL-инъекции — одна из самых опасных угроз для PHP-приложений. Узнайте, как злоумышленники используют уязвимости в коде и как защитить свою базу данных с помощью безопасных методов программирования.