Алгоритмы в программировании: что это такое, какие бывают и зачем нужны
Алгоритмы — это фундамент любой программы, без которого не обходится ни одна строка кода. По сути, они представляют собой последовательность четко определенных действий, приводящих к решению конкретной задачи. Они встречаются повсюду: от рецептов приготовления блюд до сложнейших вычислительных операций в искусственном интеллекте. Для программиста понимание алгоритмов — это не просто теоретическое знание, а практический инструмент, позволяющий писать эффективный, оптимизированный код.

В этой статье мы рассмотрим, что такое алгоритмы, какими они бывают, как устроены и почему их изучение критически важно для всех, кто работает в IT-сфере.
- Что такое алгоритм простыми словами
- Зачем нужны и где применяются
- Основные свойства
- Основные типы и виды
- Ключевые алгоритмы, которые должен знать каждый программист
- Алгоритмы работы с данными и структурами данных
- Алгоритмы на графах
- Рекурсия и динамическое программирование
- Как начать изучать алгоритмы
- Заключение
- Рекомендуем посмотреть курсы по программированию
Что такое алгоритм простыми словами
Алгоритм — это пошаговая инструкция для решения конкретной задачи. Представьте рецепт приготовления яичницы: сначала нужно разогреть сковороду, затем добавить масло, разбить яйца, посолить и дождаться готовности. Каждое действие выполняется в строгой последовательности, и результат предсказуем — если следовать инструкции, получится готовое блюдо. Точно так же работает алгоритм: он описывает порядок операций, которые приводят к нужному результату.
В программировании последовательность становится основой любого кода. Здесь важно понимать: компьютер не способен к импровизации или интуитивным решениям. Ему необходимо точно указать каждое действие — какие данные получить, как их обработать и что вывести в результате. Программист переводит задачу на язык алгоритма, разбивая её на элементарные операции, понятные машине. Например, чтобы написать программу для сложения двух чисел, нужно описать последовательность: запросить у пользователя первое число, затем второе, выполнить операцию сложения и вывести результат на экран. Без четких шагов код превращается в набор бессвязных команд, неспособных решить поставленную задачу.
Зачем нужны и где применяются
Алгоритмы нужны для того, чтобы решать задачи структурированно, получать предсказуемый результат и выявлять ошибки в работе, если он оказался неожиданным. Они нашли практическое применение во всех областях деятельности человека, где процесс должен идти по определенному плану или сценарию. Например, по ним ученые проводят исследования, врачи ставят диагнозы и назначают лечение, а логисты планируют маршруты доставки.
В IT-сфере играют ключевую роль — они составляют основу любой программы и определяют её эффективность. Давайте рассмотрим, как специалисты разных профессий используют последовательности в своей работе.
- Программисты создают код, и любой код — это, по сути, алгоритм. С его помощью можно структурировать задачи и разбить их на понятные для компьютера этапы. Разработчик перекладывает на машину действия, которые может выполнить сам, в виде последовательностей, но программа выполняет их быстрее и точнее.
- Data Scientists используют последовательности для анализа данных, выявления закономерностей и построения моделей. Например, с их помощью специалист может классифицировать информацию, определив типы клиентов компании, и спрогнозировать их отток.
- DevOps-инженеры работают внутри цикла разработки продуктов, который основан на методологии DevOps (от англ. development — «разработка» и operations — «администрирование»). Такие специалисты помогают наладить взаимодействие членов команды, создать единую инфраструктуру и автоматизировать процессы. По сути, методология DevOps — это последовательность действий команды проекта.
- Тестировщики проверяют продукт на наличие ошибок, разрабатывая алгоритмы тестирования. Их цель — найти правильные и неправильные кейсы использования программы, составить отчёт об ошибках и передать его разработчикам.
- Менеджеры проектов следят за тем, чтобы команда придерживалась последовательности работы. Например, по методологии Scrum проджект-менеджер соблюдает сроки спринтов, собирает правки от заказчика и согласовывает очередную версию продукта.
- Менеджеры по продажам также опираются на алгоритмы. Скрипты и воронка продаж — это последовательные действия и аргументы, которые позволяют достичь результата — заключения сделки.
Иллюстрация показывает, как алгоритмы используются в разных IT-профессиях — от программирования и анализа данных до тестирования и продаж. В каждой роли последовательности действий помогают решать задачи быстрее и эффективнее. Это подчёркивает, что алгоритмическое мышление важно не только для разработчиков, но и для всей команды.
Ниже представлена таблица, иллюстрирующая применение в в различных IT-профессиях:
| Профессия | Как применяются |
|---|---|
| Программист | Создание кода для решения задач, структурирование логики программы |
| Data Scientist | Анализ данных, построение прогнозных моделей, классификация информации |
| DevOps-инженер | Автоматизация процессов разработки и деплоя, настройка инфраструктуры |
| Тестировщик | Разработка алгоритмов тестирования, поиск ошибок в программном обеспечении |
| Менеджер проектов | Планирование этапов работы команды согласно методологиям (Scrum, Kanban) |
| Менеджер по продажам | Следование скриптам продаж, построение воронки конверсии клиентов |
Основные свойства
Независимо от сферы применения, алгоритмы должны соответствовать определенным свойствам, которые делают их корректными и исполнимыми.
- Конечность. Алгоритм должен приводить к конкретному результату, то есть завершаться. Например, программа в итоге решает поставленную задачу, а врач помогает пациенту излечиться. Исключение — специально созданные бесконечные последовательности, в которых не заложена результативность. Например, они используются в играх, когда игрок ничего не делает, но вокруг ходят NPC (неигровые персонажи), летают птицы и плывут облака. По сути, в этот момент выполняется бесконечная последовательность.
- Предсказуемость. Это свойство предполагает, что при одинаковых условиях последовательность приводит к одинаковому результату. К примеру, при расчёте площади треугольника со сторонами по 3, 4 и 5 см он всегда должен возвращать 6 см². Это свойство даёт возможность применять алгоритм к разным данным и понимать, что он решит эту задачу верно. Если в нём есть ошибка, он может выдать неожиданный результат. Чем выше сложность, тем более критичными могут быть последствия — достаточно вспомнить случай, когда ошибка в работе аппарата для лучевой терапии привела к тому, что люди получили повышенную долю радиации, в шесть раз превышающую норму.
- Понятность. Алгоритм должен быть описан таким образом, чтобы исполнитель — будь то человек или машина — мог его выполнить. Инструкции должны быть изложены на понятном языке и содержать только те операции, которые доступны исполнителю. Например, нельзя требовать от программы выполнить действие, для которого не написана соответствующая функция.
- Определённость. Каждый шаг должен быть чётко описан, не допуская двусмысленности или произвольной интерпретации. Исполнитель не должен гадать, что имеется в виду — каждая команда формулируется однозначно. Например, в рецепте недостаточно написать «добавьте специи по вкусу» — для компьютера это бессмысленная инструкция, так как у него нет понятия «вкус».
- Дискретность. Алгоритм состоит из отдельных, последовательных шагов. Каждое действие выполняется за конечное время, после чего происходит переход к следующему этапу. Это свойство позволяет разбивать сложные задачи на простые операции и контролировать процесс выполнения на каждом этапе.
Соблюдение этих пяти свойств гарантирует, что последовательность будет работать корректно, независимо от того, кто или что ее исполняет. Без них последовательность действий превращается в набор бессистемных команд, неспособных привести к ожидаемому результату.
Основные типы и виды
Алгоритмы классифицируются по структуре и принципу работы. Давайте рассмотрим основные виды, которые составляют фундамент программирования.
Линейные
Это самый простой тип, в котором все команды выполняются последовательно, одна за другой, без каких-либо условий или повторений. Каждый шаг выполняется ровно один раз, и порядок действий строго определён.
Примером линейного может служить простая программа для расчёта суммы двух чисел: сначала запрашиваются два числа у пользователя, затем они складываются, и результат выводится на экран. Здесь нет ветвлений или циклов — только прямая последовательность действий. Линейные алгоритмы часто используются для базовых вычислений, ввода-вывода данных и простых преобразований.
Ветвящиеся
Они используют условные конструкции типа «если — то — иначе». В зависимости от выполнения определённого условия программа выбирает один из нескольких возможных путей выполнения. Это позволяет создавать более гибкие и адаптивные решения.
Представьте последовательность работы светофора: если горит зелёный свет — можно идти, если красный — нужно остановиться. В программировании подобная логика реализуется через условные операторы. Например, при проверке возраста пользователя программа может выдать разные сообщения в зависимости от того, достиг ли человек совершеннолетия. Ветвящиеся алгоритмы незаменимы в ситуациях, когда решение зависит от текущего состояния данных или внешних факторов.
Циклические
Содержат повторяющиеся шаги, которые выполняются до тех пор, пока не будет выполнено определённое условие. Циклы позволяют избежать дублирования кода и эффективно обрабатывать большие объёмы данных.
Допустим, нам нужно найти конкретный элемент в списке. Вместо того чтобы проверять каждый вручную, мы можем использовать цикл, который будет последовательно перебирать все элементы до тех пор, пока не найдёт нужный или не достигнет конца списка. Циклы бывают двух основных типов: с предусловием (цикл выполняется, пока условие истинно) и с постусловием (цикл выполняется хотя бы один раз, а затем проверяется условие). Циклические широко применяются при работе с массивами, обработке файлов и выполнении повторяющихся вычислений.
Рекурсивные
Они представляют собой особый случай, когда функция вызывает саму себя при определённых условиях. Рекурсия позволяет элегантно решать задачи, которые естественным образом разбиваются на подзадачи того же типа.
Классический пример рекурсивного алгоритма — вычисление факториала числа. Факториал n (обозначается n!) — это произведение всех натуральных чисел от 1 до n. Рекурсивное определение выглядит так: если n = 1, то результат равен 1; иначе результат = n, умноженному на факториал (n-1). Функция вызывает сама себя с уменьшенным значением до тех пор, пока не достигнет базового случая.

Иллюстрация наглядно показывает, как работает рекурсия на примере вычисления факториала. Функция последовательно вызывает саму себя, пока не достигает базового случая. Затем результаты возвращаются обратно по цепочке вызовов, формируя итоговое значение.
Другой популярный пример — числа Фибоначчи, где каждое следующее число равно сумме двух предыдущих. Рекурсивный подход позволяет записать это определение буквально в нескольких строках кода. Однако важно помнить, что рекурсия может быть неэффективной для больших значений из-за глубоких вызовов функций, и в таких случаях часто применяются методы оптимизации, такие как динамическое программирование.
Ключевые алгоритмы, которые должен знать каждый программист
Существует набор фундаментальных алгоритмов, знание которых считается обязательным для любого программиста. Эти последовательности используются повсеместно — от разработки веб-приложений до создания систем искусственного интеллекта. Давайте рассмотрим наиболее важные из них.
Алгоритмы сортировки
Сортировка — это когда элементы приводят в нужный порядок, например по возрастанию или убыванию. Наиболее распространённые последовательности сортировки включают несколько базовых подходов, каждый из которых имеет свои преимущества и недостатки.
- Пузырьковая сортировка (Bubble Sort) — простой, но неэффективный алгоритм, который сравнивает соседние элементы и меняет их местами, если они находятся в неправильном порядке. Он имеет сложность O(n²), что делает его непригодным для больших массивов данных. Однако он часто используется для обучения основам сортировки из-за своей простоты.
- Сортировка вставками (Insertion Sort) работает по принципу последовательного добавления элементов в уже отсортированную часть массива. Эта последовательность также имеет сложность O(n²), но работает быстрее на почти отсортированных массивах. Он часто используется в ситуациях, когда массивы небольшие или почти отсортированы.
- Быстрая сортировка (Quick Sort) — рекурсивный, который делит массив на подмассивы и сортирует их независимо друг от друга. Быстрая сортировка имеет среднюю сложность O(n log n) и является одним из самых эффективных алгоритмов сортировки для больших массивов данных. Однако в худшем случае её сложность может достигать O(n²).
- Сортировка слиянием (Merge Sort) делит массив на две половины, сортирует их и затем объединяет. Он имеет сложность O(n log n) и является стабильным, что означает, что он сохраняет порядок одинаковых элементов. Сортировка слиянием часто используется в ситуациях, когда требуется стабильность и предсказуемая производительность.
Ниже представлена сравнительная таблица алгоритмов сортировки:
| Тип сортировки | Сложность (средняя) | Описание | Когда использовать |
|---|---|---|---|
| Пузырьковая (Bubble Sort) | O(n²) | Сравнивает соседние элементы и меняет их местами | Для обучения, небольших массивов |
| Вставками (Insertion Sort) | O(n²) | Добавляет элементы в отсортированную часть | Почти отсортированные данные, малые массивы |
| Быстрая (Quick Sort) | O(n log n) | Рекурсивное разделение и сортировка подмассивов | Большие массивы, когда нужна скорость |
| Слиянием (Merge Sort) | O(n log n) | Разделяет массив пополам и объединяет | Когда нужна стабильность и предсказуемость |
Алгоритмы поиска
Поиск — это процесс нахождения элемента в структуре данных. Основные включают два фундаментальных подхода.
Линейный поиск (Linear Search) — простая последовательность, которая поочередно проверяет каждый элемент массива. Он имеет сложность O(n) и подходит для небольших массивов или неотсортированных данных. Он прост в реализации, но неэффективен для больших объёмов данных.
Бинарный поиск (Binary Search) — эффективная последовательность, которая работает только на отсортированных массивах. Он делит массив пополам и ищет элемент в соответствующей половине. Бинарный поиск имеет сложность O(log n) и является одним из самых быстрых алгоритмов поиска для отсортированных данных. Он часто используется в сочетании с сортировкой для повышения общей производительности.
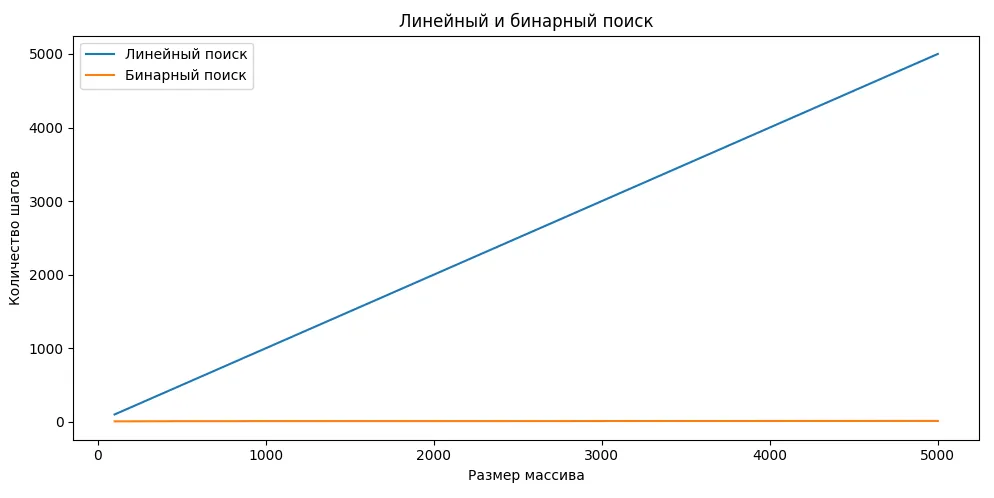
График сравнивает количество шагов, необходимых для линейного и бинарного поиска. Линейный поиск проверяет элементы по очереди, поэтому его сложность растёт вместе с массивом. Бинарный поиск требует значительно меньше шагов, но работает только с отсортированными данными.
Вот простой пример реализации бинарного поиска на Python:
def binary_search(arr, target): left, right = 0, len(arr) - 1 while left <= right: mid = (left + right) // 2 if arr[mid] == target: return mid # Элемент найден elif arr[mid] < target: left = mid + 1 else: right = mid - 1 return -1 # Элемент не найден
На основе этих базовых алгоритмов работают системы искусственного интеллекта и анализа данных. Понимание принципов сортировки и поиска позволяет программистам создавать эффективные решения для обработки больших объёмов информации.
Алгоритмы работы с данными и структурами данных
Структуры данных — это способы организации и хранения информации, а последовательности определяют, как с этими данными работать. Эффективность программы во многом зависит от правильного выбора структуры и соответствующих алгоритмов для работы с ней. Давайте рассмотрим основные виды и типичные операции с ними.
Массивы (Arrays)
Массивы представляют собой коллекцию элементов, доступ к которым осуществляется по индексу. Это одна из самых простых и распространённых структур данных. Основные операции с массивами включают доступ к элементу по индексу (сложность O(1)), поиск (O(n) для неотсортированного массива), добавление элемента в конец (O(1) в среднем) и удаление (O(n), так как требуется сдвиг остальных элементов).
Массивы эффективны, когда нужен быстрый доступ к элементам по индексу, но их размер обычно фиксирован или требует затратных операций для изменения. Они идеально подходят для хранения упорядоченных данных, когда известно примерное количество элементов.
Связные списки (Linked Lists)
Связные списки состоят из узлов, каждый из которых содержит данные и ссылку на следующий узел. В отличие от массивов, элементы связного списка не обязательно располагаются в памяти последовательно. Основные операции включают обход списка (O(n)), добавление элемента в начало или конец (O(1)), удаление элемента (O(1), если известен узел, или O(n) для поиска).
Связные списки позволяют легко добавлять и удалять элементы, но обход списка может быть медленным из-за последовательного доступа к элементам. Они особенно полезны, когда размер данных заранее неизвестен и часто изменяется.
Стэки и очереди (Stacks and Queues)
Стэк работает по принципу LIFO (Last In, First Out — последним пришёл, первым ушёл). Основные операции: добавление (push) и удаление элемента (pop), обе выполняются за O(1). Стэки часто используются для реализации рекурсии, отмены действий (undo) и хранения временных данных. Они позволяют быстро добавлять и удалять элементы, но не подходят для случайного доступа к данным.
Очередь работает по принципу FIFO (First In, First Out — первым пришёл, первым ушёл). Операции с очередью: добавление элемента (enqueue) и удаление элемента (dequeue), также выполняются за O(1). Очереди используются для управления задачами в порядке их поступления — например, в системах обработки запросов или планировщиках задач операционной системы.
Хеш-таблицы (Hash Tables)
Хеш-таблицы используют хеш-функции для преобразования ключей в индексы массива, что позволяет выполнять операции вставки, удаления и поиска элементов за среднее время O(1). Это делает их чрезвычайно эффективными для работы с большими объёмами данных, когда требуется быстрый доступ по ключу.
Хеш-таблицы широко применяются в базах данных, кэшировании, индексации и реализации ассоциативных массивов (словарей). Однако в худшем случае, при коллизиях хеш-функции, производительность может снизиться до O(n). Для минимизации коллизий используются различные способы разрешения конфликтов, такие как метод цепочек или открытая адресация.
Выбор подходящей структуры данных критически важен для оптимизации производительности программы. Понимание того, как работают массивы, списки, стэки, очереди и хеш-таблицы, позволяет программистам писать более эффективный код и решать задачи с минимальными затратами вычислительных ресурсов.
Алгоритмы на графах
Графы — это структуры данных, состоящие из узлов (вершин) и рёбер (связей между узлами). Они позволяют моделировать сложные системы и находить оптимальные пути и связи между элементами. Графы широко используются в различных областях — от компьютерных до социальных сетей и систем навигации.
Определение графа, вершины и рёбра. Граф состоит из множества вершин и рёбер, соединяющих эти вершины. Первые представляют собой объекты (например, города, пользователей или узлы сети), а вторые — связи между ними (дороги, дружеские отношения или сетевые соединения).
В ориентированных графах у связей есть направление — как у дорог с односторонним движением. В неориентированных направление не важно, связь работает в обе стороны. Также у связей может быть вес — число, которое показывает, например, расстояние, время или стоимость перехода.
Применения графов. Графы находят применение в самых разных сферах. В компьютерных сетях они моделируют структуру соединений между устройствами, позволяя оптимизировать маршрутизацию данных. В социальных сетях графы представляют пользователей и их связи, что помогает анализировать сообщества и рекомендовать новых друзей. В навигационных системах графы используются для представления дорожных сетей и поиска кратчайших маршрутов между точками. Также графы применяются в планировании проектов, анализе зависимостей задач и оптимизации логистических цепочек.
Алгоритмы работы с графами
Существует несколько ключевых видов для работы с графами, каждый из которых решает определённый класс задач.
- Поиск в глубину (DFS — Depth-First Search) — рекурсивный алгоритм, который посещает все вершины графа, начиная с одной вершины и углубляясь в каждую ветвь до конца. DFS используется для поиска путей, проверки связности графа и решения задач, связанных с обходом графа. Хорошо подходит для задач, где нужно исследовать все возможные варианты до конца, прежде чем вернуться назад.
- Поиск в ширину (BFS — Breadth-First Search) — алгоритм, который посещает все вершины графа на одном уровне, прежде чем перейти к следующему уровню. BFS используется для поиска кратчайших путей в неориентированных графах без весов и решения задач, связанных с обходом графа по уровням. Он особенно эффективен, когда нужно найти минимальное количество шагов между двумя вершинами.
- Алгоритм Дейкстры (Dijkstra’s Algorithm) находит кратчайший путь от одной вершины до всех остальных в графе с неотрицательными весами рёбер. Широко используется в задачах маршрутизации и планирования путей — например, в навигационных приложениях для поиска оптимального маршрута между городами с учётом расстояний.
- Алгоритм Флойда-Уоршелла (Floyd-Warshall Algorithm) находит кратчайшие пути между всеми парами вершин в графе. Используется для решения задач, связанных с нахождением кратчайших путей в графах с различными весами рёбер, включая отрицательные веса (но без отрицательных циклов). Флойд-Уоршелл особенно удобен, когда необходимо построить полную матрицу расстояний между всеми вершинами графа.
Понимание алгоритмов работы с графами открывает широкие возможности для решения сложных задач оптимизации, анализа сетей и моделирования взаимосвязей в различных системах.
Рекурсия и динамическое программирование
Рекурсия и динамическое программирование — это мощные техники оптимизации алгоритмов, которые позволяют решать сложные задачи, разбивая их на более простые подзадачи. Давайте разберёмся, как они работают и когда их стоит применять.
Что такое рекурсия
Рекурсия — это метод, при котором функция вызывает сама себя для решения задачи. Рекурсивный подход естественен для задач, которые можно разделить на подзадачи того же типа. Классический пример — вычисление факториала числа.
Факториал n (обозначается n!) — это произведение всех натуральных чисел от 1 до n. Например, 5! = 5 × 4 × 3 × 2 × 1 = 120. Рекурсивное определение выглядит просто: если n = 1, результат равен 1 (базовый случай); иначе результат = n, умноженному на факториал (n-1). Функция продолжает вызывать саму себя с уменьшающимся значением до тех пор, пока не достигнет базового случая.
Другой популярный пример рекурсии — числа Фибоначчи, где каждое следующее число равно сумме двух предыдущих (0, 1, 1, 2, 3, 5, 8, 13…). Рекурсивная реализация выглядит элегантно: если n равно 0 или 1, возвращаем n; иначе возвращаем сумму двух предыдущих чисел Фибоначчи.
Почему рекурсия может быть неэффективной
Несмотря на элегантность, рекурсия может оказаться крайне неэффективной. Рассмотрим вычисление чисел Фибоначчи: для вычисления F(5) функция вызовет F(4) и F(3), но F(4) в свою очередь вызовет F(3) и F(2), то есть F(3) будет вычислено дважды. При увеличении n количество повторных вычислений растёт экспоненциально, что делает наивную рекурсию непригодной для больших значений.
Кроме того, каждый рекурсивный вызов занимает место в стеке вызовов, и при глубокой рекурсии можно столкнуться с переполнением стека. Эти проблемы делают чистую рекурсию малопригодной для практического использования во многих случаях.
Что такое динамическое программирование
Динамическое программирование — это метод оптимизации, который разбивает сложную задачу на более простые подзадачи и сохраняет результаты их решения для повторного использования. Основная идея заключается в том, чтобы избежать повторных вычислений одних и тех же подзадач, что резко повышает эффективность.
Существует два основных подхода в динамическом программировании: мемоизация (запоминание результатов) и табуляция (заполнение таблицы снизу вверх). Мемоизация сохраняет результаты уже вычисленных подзадач в специальной структуре данных (например, в словаре или массиве), чтобы при повторном обращении сразу вернуть сохранённое значение. Табуляция итеративно заполняет таблицу результатов от базовых случаев к искомому значению.
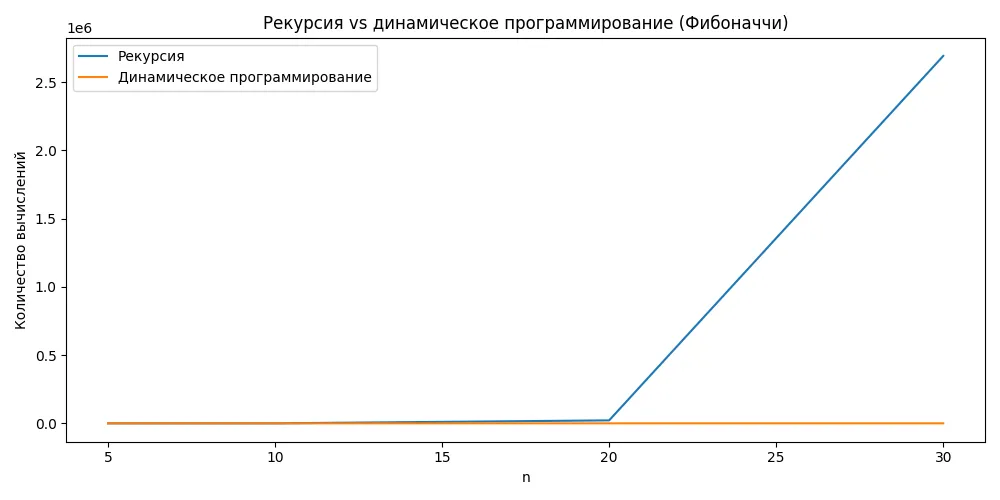
Диаграмма иллюстрирует разницу в количестве вычислений при наивной рекурсии и динамическом программировании на примере чисел Фибоначчи. При рекурсии количество повторных вычислений растёт очень быстро. Динамическое программирование устраняет эти повторы за счёт сохранения промежуточных результатов.
Применяя мемоизацию к задаче о числах Фибоначчи, мы сохраняем каждое вычисленное значение и при повторном запросе сразу возвращаем его из памяти. Это снижает сложность с экспоненциальной O(2^n) до линейной O(n).
Примеры задач динамического программирования
Задача о рюкзаке (Knapsack Problem) — классическая история оптимизации, где нужно найти максимальную стоимость предметов, которые можно поместить в рюкзак ограниченной вместимости. Динамическое программирование позволяет эффективно решить эту задачу, сохраняя результаты промежуточных вычислений и избегая повторного решения одних и тех же подзадач. Решение строится путём заполнения таблицы, где каждая ячейка представляет оптимальное решение для подзадачи с определённым весом и набором предметов.
Задача о наибольшей общей подпоследовательности — это поиск самой длинной последовательности элементов, которая встречается в двух наборах данных в одном и том же порядке. Её используют, например, для сравнения ДНК, поиска различий между версиями файлов и проверки текстов на плагиат. Обычно эту задачу решают с помощью динамического программирования: сложную задачу разбивают на простые части и запоминают промежуточные результаты, чтобы не считать их заново.
Как начать изучать алгоритмы
Изучение алгоритмов может показаться сложной задачей, особенно для начинающих программистов. Однако при правильном подходе освоить эту тему вполне реально. Давайте рассмотрим, с чего стоит начать и какие ресурсы помогут в обучении.
Начните с визуализации
Один из самых эффективных способов понять алгоритмы — визуализировать их работу. Блок-схемы помогают представить последовательность действий в графическом виде, где каждый шаг изображён в виде геометрической фигуры, соединённой стрелками. Овал обозначает начало и конец последовательности, параллелограмм — ввод или вывод данных, а ромб — условие, определяющее дальнейший ход выполнения.
Рисование блок-схем развивает алгоритмическое мышление и помогает разобраться в логике работы программы ещё до написания кода. Существуют специальные онлайн-инструменты для создания блок-схем, а также интерактивные платформы, которые позволяют наблюдать за выполнением последовательностей в в реальном времени — например, визуализаторы сортировок показывают, как элементы массива перемещаются на каждом шаге.
Практикуйтесь на простых языках программирования
Для изучения хорошо подходят языки Python и JavaScript благодаря их простому синтаксису и наглядности. Python особенно популярен в образовательных целях — его код читается почти как обычный текст, что позволяет сосредоточиться на логике алгоритма, а не на особенностях языка. JavaScript удобен тем, что работает прямо в браузере, и результаты можно увидеть мгновенно.
Начинать стоит с реализации простейших последовательностей: сложение двух чисел, поиск максимального элемента в массиве, проверка числа на чётность. Постепенно переходите к более сложным задачам — сортировкам, поиску, работе со строками. Важно не просто копировать готовые решения, а пытаться написать код самостоятельно, даже если это займёт больше времени.
Решайте задачи на специализированных платформах
Практика — ключ к освоению. Существует множество платформ, где можно тренироваться в решении задач разного уровня сложности:
- LeetCode — одна из самых популярных платформ с огромной базой задач, от простых до сложных. Многие задачи взяты из реальных собеседований в крупных IT-компаниях.
- Codeforces — платформа для спортивного программирования с регулярными соревнованиями и обширным архивом задач.
- HackerRank — ресурс с задачами по алгоритмам, структурам данных и другим разделам computer science.
- CodeWars — геймифицированная платформа, где задачи называются «ката» и имеют разные уровни сложности.
Начните с простых задач и постепенно повышайте сложность. Не бойтесь смотреть на чужие решения после того, как попытались решить задачу самостоятельно — это помогает учиться на примерах других программистов и узнавать новые подходы.
Изучайте теорию параллельно с практикой
Решение задач должно сопровождаться изучением теоретических основ. Понимание сложности алгоритмов (нотация Big O), принципов работы различных структур данных и классических алгоритмических подходов даёт прочный фундамент. Существуют отличные книги и онлайн-курсы, посвящённые алгоритмам.
Главное — не торопиться и двигаться последовательно. Алгоритмы — это не то, что можно выучить за неделю. Регулярная практика, постепенное усложнение задач и глубокое понимание базовых концепций со временем приведут к уверенному владению этой важнейшей областью программирования.
Заключение
Алгоритмы — это основа любого кода, фундамент, на котором строится всё современное программное обеспечение. Без понимания невозможно создавать эффективные, масштабируемые и надёжные решения. Давайте подведем итоги:
-
Алгоритмы в программировании лежат в основе любого кода. Они задают порядок действий и определяют результат работы программы.
-
Каждый алгоритм должен обладать конечностью, определённостью и понятностью. Эти свойства обеспечивают корректное выполнение инструкций.
-
В программировании используются разные типы алгоритмов. Линейные, ветвящиеся, циклические и рекурсивные решают разные классы задач.
-
Алгоритмы применяются во всех IT-профессиях. Они используются в разработке, анализе данных, тестировании и управлении процессами.
-
Выбор алгоритма влияет на производительность программы. Неэффективные решения приводят к лишним затратам ресурсов.
-
Изучение алгоритмов развивает алгоритмическое мышление. Оно помогает быстрее находить оптимальные решения задач.
Если вы только начинаете осваивать профессию программиста, рекомендуем обратить внимание на подборку курсов по программированию. В них сочетается теоретическая база по алгоритмам и практическая часть с решением реальных задач, что помогает быстрее закрепить знания на практике.
Рекомендуем посмотреть курсы по программированию
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Специалист DevSecOps
|
Академия АйТи
17 отзывов
|
Цена
149 000 ₽
|
|
Длительность
1 месяц
|
Старт
скоро
|
Подробнее |

Тест-дизайн без воды: что работает на практике
Какие техники тест-дизайна действительно помогают находить баги, а какие — только усложняют жизнь? Рассказываем на конкретных примерах с чек-листами и рекомендациями.

Docker-репозитории: полное руководство по работе, настройке и публикации образов
Docker репозиторий образов — ключевой элемент современной контейнерной инфраструктуры. Как выбрать подходящий вариант, безопасно хранить образы и не запутаться в push и pull? В статье — понятные объяснения и практические примеры.

Как убрать лишнюю страницу в Word
Сталкивались с тем, что пустая страница в документе никак не удаляется? В этом разборе мы подробно объясняем, как удалить страницу в ворде, почему появляются лишние листы и какие инструменты помогают убрать их за пару минут. Читайте, чтобы разобраться в причинах и сразу применить простые решения.