Что такое факториал и как его вычислить
Факториал — одно из тех математических понятий, которое, несмотря на кажущуюся простоту, играет фундаментальную роль в различных областях науки и технологий. От комбинаторики до теории вероятностей, от анализа алгоритмов до машинного обучения — всюду мы встречаем это элегантное математическое выражение. В этом курсе мы разберемся, что такое факториал, как его правильно вычислять и почему это понятие так важно в современной науке.

Также вы узнаете, где факториал применяется на практике: в расчёте перестановок и сочетаний, в оценке сложности алгоритмов, в статистике и даже в вычислительных методах физики и биоинформатики.
- Что такое факториал: определение и основные понятия
- Свойства и особенности
- Области применения факториала
- Как вычислить factorial: пошаговые примеры и алгоритмы
- Часто возникающие ошибки и проблемы
- Ошибки при использовании рекурсивных функций
- Таблица факториалов: от 1 до 20
- Заключение
- Рекомендуем посмотреть курсы по программированию на PHP
Что такое факториал: определение и основные понятия
Факториал натурального числа n — это произведение всех натуральных чисел от 1 до n включительно. Обозначается это математическое понятие восклицательным знаком после числа: n! (читается как «эн факториал»).
Формально его можно записать следующим образом:
n! = n × (n-1) × (n-2) × … × 2 × 1
Рассмотрим простой пример: вычислим factorial числа 5. 5! = 5 × 4 × 3 × 2 × 1 = 120
В математике существует важное соглашение: факториал нуля равен единице (0! = 1). Это определение может показаться странным, но оно необходимо для согласованности математических формул, особенно в комбинаторике и теории вероятностей.
Важно отметить, что factorial определён только для неотрицательных целых чисел. Такие выражения как (-3)! или (2,5)! в стандартной математике не имеют определения (хотя в продвинутой математике существует обобщение факториала —гамма-функция, которая может работать и с другими типами чисел).
Для удобства приведем таблицу значений факториалов небольших чисел:
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
Как видно из таблицы, факториал растет чрезвычайно быстро с увеличением числа n, что делает его вычисление для больших чисел нетривиальной задачей.
История и происхождение факториала
Несмотря на свою внешнюю простоту, факториал имеет богатую математическую биографию. Первые упоминания встречаются ещё в работах математиков XVIII века, когда активно развивалась комбинаторика и теория вероятностей. Одним из первых, кто использовал подобное произведение натуральных чисел, был Абрахам де Муавр, а позже — Леонард Эйлер и Жозеф Луи Лагранж.
Однако обозначение восклицательным знаком (!) появилось не сразу. Оно впервые было предложено французским математиком Кристианом Крампом в 1808 году и прижилось благодаря своей лаконичности и визуальной выразительности. С тех пор n! стало универсальным обозначением, которое легко узнается как в школьных учебниках, так и в научных публикациях.
Важно понимать, что идея факториала возникла не как абстрактная формула, а как ответ на практический вопрос: «Сколькими способами можно упорядочить объекты?». И именно в этом прикладном значении началась его математическая карьера.
Свойства и особенности
При работе с факториалами необходимо учитывать несколько ключевых свойств, которые делают их столь полезными в различных областях математики и программирования. Рассмотрим наиболее важные из них.
Одно из фундаментальных свойств — его рекуррентность. Это означает, что factorial числа n можно выразить через факториал предыдущего числа:
n! = n × (n-1)!
Данное соотношение чрезвычайно полезно как для теоретических выкладок, так и для практических вычислений. Например, зная, что 4! = 24, мы можем легко вычислить 5!: 5! = 5 × 4! = 5 × 24 = 120
Важно помнить, что factorial не определён для отрицательных чисел. Если мы попытаемся вычислить, например, (-3)!, то столкнемся с математической неопределенностью. В контексте программирования попытка вычислить факториал отрицательного числа обычно приводит к ошибке или некорректному результату.
Для вычисления больших чисел используется приближенная формула Стирлинга:
n! ≈ √(2πn) × (n/e)^n
Где e — основание натурального логарифма (приблизительно 2,718), а π — число пи (приблизительно 3,14159).
Формула Стирлинга дает тем более точное приближение, чем больше значение n. Для n = 10 погрешность составляет менее 1%, а для бо́льших n она становится еще меньше. Это свойство делает формулу Стирлинга незаменимой при работе с факториалами больших чисел, когда прямое вычисление становится вычислительно сложным или невозможным.
Еще одна особенность — чрезвычайно быстрый рост. Эта функция растет быстрее любой экспоненциальной функции, что создает определённые вычислительные ограничения даже для современных компьютеров.
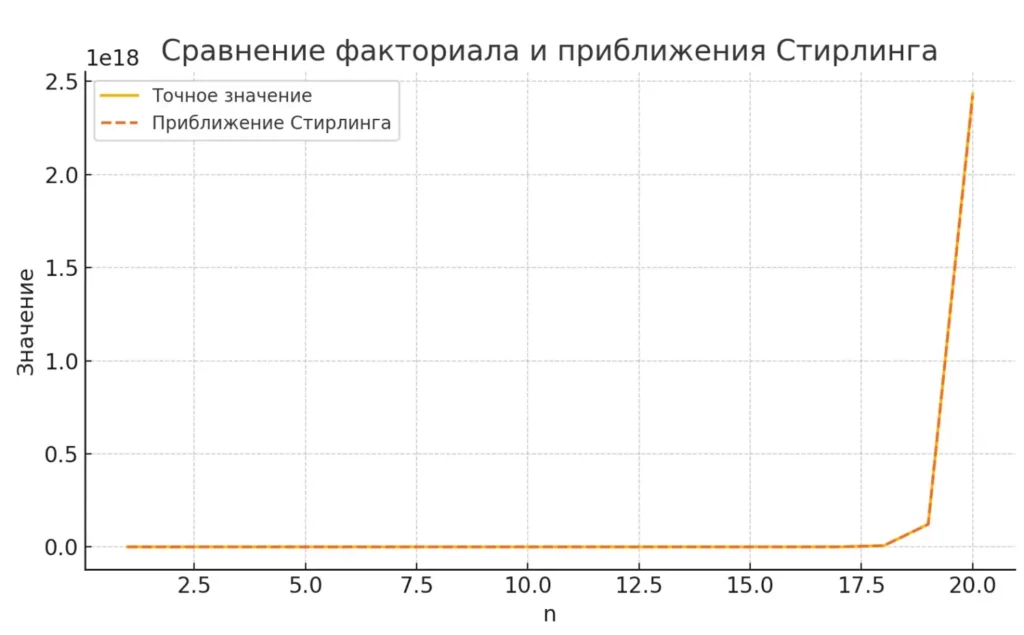
Сравнение точного значения факториала и приближённого вычисления по формуле Стирлинга.
Рекуррентная формула
Рекуррентная формула — это выражение, которое определяет математическую функцию через её же значения для предыдущих аргументов. В случае с факториалом, это свойство позволяет нам определить n! через (n-1)!, что открывает интересные возможности, особенно в программировании.
Как мы уже отметили, рекуррентная формула выглядит следующим образом: n! = n × (n-1)!
При этом в качестве базового случая используется значение 0! = 1 или 1! = 1.
Рекурсивный подход особенно элегантно реализуется в программировании. Для примера, напишем функцию вычисления factorial на языке Python:
def factorial(n): # Базовый случай: факториал 0 или 1 равен 1 if n == 0 or n == 1: return 1 # Рекурсивный случай: вычисляем через предыдущее значение else: return n * factorial(n-1) # Пример использования print(factorial(5)) # Вывод: 120
Этот код наглядно демонстрирует, как работает рекурсия: функция вызывает саму себя с уменьшенным аргументом до тех пор, пока не достигнет базового случая. Затем результаты «разворачиваются» в обратном порядке, формируя итоговое произведение.
Однако стоит помнить, что рекурсивный подход, хоть и элегантен, имеет свои ограничения — в частности, ограничение на глубину рекурсии и дополнительные накладные расходы на вызовы функций, что может привести к проблемам при работе с большими числами.

Рекурсия как лестница — каждый шаг зависит от предыдущего: n! = n × (n-1)!
Быстрое возрастание
Одна из самых примечательных характеристик — экстремально быстрый рост значений с увеличением аргумента. Эта особенность делает factorial своеобразным «чемпионом» среди математических функций по скорости роста, опережающим даже экспоненциальные функции.
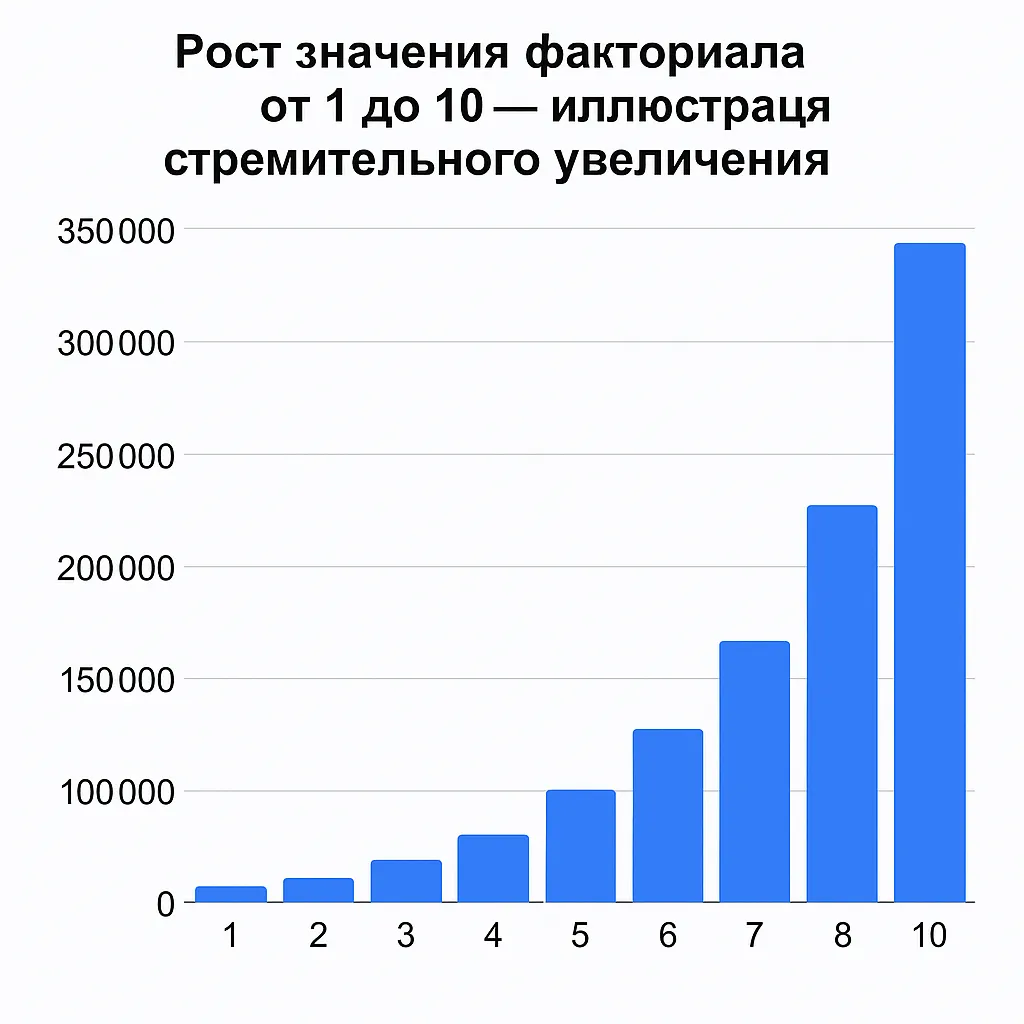
Рост значения факториала от 1 до 10 — иллюстрация стремительного увеличения.
Давайте проиллюстрируем это на конкретных примерах:
10! = 3 628 800 (более 3.6 миллионов) 15! = 1 307 674 368 000 (более 1.3 триллионов) 20! = 2 432 902 008 176 640 000 (около 2.4 квинтиллионов)
Если представить эти числа графически, мы увидим, что кривая роста факториала устремляется вверх практически вертикально после n>10. Это означает, что уже для относительно небольших чисел (n>20) значения factorial становятся настолько большими, что превышают возможности стандартных числовых типов в большинстве языков программирования.
В алгоритмической сложности существует специальное обозначение O(n!), которое используется для алгоритмов с факториальной сложностью. Это именно те алгоритмы, которых стараются избегать программисты, поскольку даже для небольших входных данных время выполнения таких алгоритмов становится практически неприемлемым для практических приложений. Рост значения факториала от 1 до 10 — иллюстрация стремительного увеличения.
Рост значения факториала от 1 до 10 — иллюстрация стремительного увеличения.
Области применения факториала
Несмотря на кажущуюся простоту определения, factorial находит применение в самых разных областях математики и прикладных науках. Рассмотрим основные сферы, где это математическое понятие играет ключевую роль.
Комбинаторика
Пожалуй, наиболее естественная область применения факториалов — комбинаторика, наука о подсчете различных комбинаций элементов. Здесь factorial лежит в основе многих формул:
- Перестановки без повторений. Количество способов расположить n различных объектов в определенном порядке равно n!. Например, 5 различных книг можно расставить на полке 5! = 120 различными способами.
- Сочетания. Число способов выбрать k объектов из n без учета порядка вычисляется по формуле: C(n,k) = n! / (k! × (n-k)!)
Например, число способов выбрать команду из 3 человек из группы в 10 человек: C(10,3) = 10! / (3! × 7!) = 120
Задача: На банкет приглашены 6 человек. Сколькими способами их можно рассадить за круглым столом? Решение: Поскольку стол круглый, имеет значение только относительное расположение гостей. Поэтому число перестановок будет равно (6-1)! = 5! = 120 способов.
Теория вероятностей и статистика
В теории вероятностей факториалы используются для вычисления вероятностей сложных событий:
- Биномиальное распределение. Вероятность получить ровно k успехов в n независимых испытаниях с вероятностью успеха p: P(X = k) = C(n,k) × p^k × (1-p)^(n-k), где C(n,k) выражается через факториалы.
- Распределение Пуассона. Вероятность того, что в фиксированном промежутке произойдет ровно k событий: P(X = k) = (λ^k × e^(-λ)) / k!, где λ — среднее число событий, e — число Эйлера.
Задача: В группе из 20 студентов случайным образом выбирают 3 человек для участия в олимпиаде. Какова вероятность, что будут выбраны определенные три студента? Решение: Всего способов выбрать 3 студентов из 20: C(20,3) = 20! / (3! × 17!) = 1140. Вероятность выбора конкретных трех студентов: 1/1140 ≈ 0,000877.
Математический анализ
В математическом анализе факториалы появляются в разложениях функций в ряды:
- Ряд Тейлора. Например, для функции e^x: e^x = 1 + x + x²/2! + x³/3! + … + x^n/n! + …
- Ряд Маклорена. Частный случай ряда Тейлора, когда разложение ведется в окрестности точки x = 0.
Факториалы также играют важную роль в асимптотическом анализе функций и в теории специальных функций, таких как гамма-функция — обобщение factorial на нецелые аргументы.
Программирование и алгоритмы
В программировании он часто используется как пример для иллюстрации рекурсивных алгоритмов, а также при анализе сложности алгоритмов. Алгоритмы с факториальной сложностью O(n!) считаются одними из самых «тяжелых» с вычислительной точки зрения. Классический пример — задача коммивояжера (при полном переборе).
Применение factorial не ограничивается теоретическими выкладками — они активно используются в криптографии, теории кодирования, анализе данных и даже в задачах генетики и анализа ДНК, где комбинаторные методы позволяют исследовать всевозможные комбинации генов.
Как вычислить factorial: пошаговые примеры и алгоритмы
В этом разделе мы рассмотрим различные методы вычисления — от простых ручных расчетов до программных реализаций. Независимо от вашего уровня подготовки, эти подходы позволят эффективно работать с факториалами в различных контекстах.
Вычисление вручную
Вычисление факториала вручную довольно просто — достаточно последовательно перемножить все числа от 1 до n.
Пример вычисления 5!:
1. Запишем определение: 5! = 5 × 4 × 3 × 2 × 1
2. Выполним умножение поэтапно:
- 5 × 4 = 20
- 20 × 3 = 60
- 60 × 2 = 120
- 120 × 1 = 120
3. Получаем результат: 5! = 120
Пример вычисления 7!:
1. Запишем определение: 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
2. Выполним умножение поэтапно:
- 7 × 6 = 42
- 42 × 5 = 210
- 210 × 4 = 840
- 840 × 3 = 2520
- 2520 × 2 = 5040
- 5040 × 1 = 5040
3. Получаем результат: 7! = 5040
При вычислении вручную можно также использовать уже известные значения меньших факториалов. Например, зная, что 6! = 720, мы можем просто умножить это значение на 7, чтобы получить 7!: 7! = 7 × 6! = 7 × 720 = 5040
Вычисление с помощью рекурсии в программировании
Как мы уже отмечали ранее, рекурсивный подход особенно элегантно реализуется в программировании. Приведем более детальную реализацию на Python:
def factorial_recursive(n):
# Проверка входных данных
if n < 0:
return "Факториал не определен для отрицательных чисел"
# Базовый случай
if n == 0 or n == 1:
return 1
# Рекурсивный случай
return n * factorial_recursive(n - 1)
# Тестирование функции
print(f"5! = {factorial_recursive(5)}") # Вывод: 5! = 120
print(f"7! = {factorial_recursive(7)}") # Вывод: 7! = 5040
Рекурсивное решение интуитивно понятно и близко к математическому определению factorial, однако оно имеет два существенных ограничения:
- Ограниченная глубина рекурсии (в Python по умолчанию около 1000).
- Дополнительный расход памяти на каждый рекурсивный вызов.
Вычисление через цикл
Итеративный подход лишен недостатков рекурсии и обычно более эффективен:
def factorial_iterative(n):
# Проверка входных данных
if n < 0:
return "Факториал не определен для отрицательных чисел"
# Обработка базовых случаев
if n == 0 or n == 1:
return 1
# Итеративное вычисление
result = 1
for i in range(2, n + 1):
result *= i
return result
# Тестирование функции
print(f"10! = {factorial_iterative(10)}") # Вывод: 10! = 3628800
Преимущества итеративного подхода:
- Отсутствие ограничений на глубину рекурсии.
- Меньшее потребление памяти.
- Как правило, более высокая производительность.
Недостатки:
- Менее элегантная реализация по сравнению с рекурсивным подходом.
Вычисление больших факториалов
Для вычисления factorial больших чисел в Python можно использовать встроенную библиотеку math:
import math
# Вычисление факториала с помощью встроенной функции
result = math.factorial(20)
print(f"20! = {result}") # Вывод: 20! = 2432902008176640000

Скриншот подчеркивает, что Python уже содержит встроенный безопасный способ вычисления факториалов, не требующий ручного кода.
Для еще больших чисел, которые могут превышать возможности стандартных типов данных, мы можем использовать приближенные формулы, такие как формула Стирлинга:
import math
def stirling_approximation(n):
# Формула Стирлинга: n! ≈ √(2πn) × (n/e)^n
return math.sqrt(2 * math.pi * n) * (n / math.e) ** n
# Сравнение точного значения и приближения Стирлинга
n = 10
exact = math.factorial(n)
approximation = stirling_approximation(n)
print(f"Точное значение {n}!: {exact}")
print(f"Приближение Стирлинга: {approximation}")
print(f"Погрешность: {abs(exact - approximation) / exact * 100:.2f}%")
Для работы с действительно большими числами в Python есть тип данных decimal, который позволяет работать с числами произвольной точности:
from decimal import Decimal, getcontext
# Установим высокую точность вычислений
getcontext().prec = 100
def big_factorial(n):
if n < 0:
return "Факториал не определен для отрицательных чисел"
result = Decimal(1)
for i in range(2, n + 1):
result *= i
return result
# Вычисление большого факториала
print(f"50! = {big_factorial(50)}")
Выбор метода вычисления факториала зависит от конкретной задачи, доступных вычислительных ресурсов и требуемой точности результата.
Часто возникающие ошибки и проблемы
При работе с факториалами в программировании и вычислительной математике возникает ряд типичных проблем, о которых следует знать заранее. Рассмотрим наиболее распространённые из них и способы их преодоления.
Переполнение памяти при больших числах
Одна из самых распространённых проблем — переполнение стандартных числовых типов. Учитывая быстрый рост factorial, даже относительно небольшие значения n могут привести к числам, которые не помещаются в стандартные типы данных.
# Пример переполнения в языках с ограничением размера целых чисел
# (не в Python, там автоматическая работа с большими числами)
# На C++ или Java:
int result = 1;
for (int i = 2; i <= 20; i++) {
result *= i; // На 13-ой итерации произойдёт переполнение для типа int
}
Решение:
- Использование специальных типов для работы с большими числами (BigInteger в Java, библиотека GMP в C++, встроенная поддержка произвольной точности в Python).
- Для аналитических задач — использование логарифмического представления (ln(n!)).
- Применение приближенных формул для оценки (формула Стирлинга).
Ошибки при использовании рекурсивных функций
Рекурсивные реализации вычисления факториала сталкиваются с двумя основными проблемами:
Ограничение глубины рекурсии:
# При вызове с большим аргументом будет ошибка: # RecursionError: maximum recursion depth exceeded factorial_recursive(1500) # Превышение максимальной глубины рекурсии
Избыточные вычисления при неоптимальной реализации: наивная рекурсивная реализация может выполнять одни и те же вычисления многократно, что снижает производительность.
Решение:
- Использование итеративного подхода вместо рекурсивного.
- Применение методов мемоизации для сохранения промежуточных результатов.
- В Python — увеличение лимита рекурсии (хотя это не рекомендуется как основное решение):
import sys sys.setrecursionlimit(5000) # Увеличение лимита рекурсии
Потеря точности в приближенных вычислениях
При использовании приближенных формул (например, формулы Стирлинга) неизбежно возникает погрешность вычислений, особенно заметная для небольших значений n.
Решение:
- Использование точных методов для малых n.
- Применение поправочных коэффициентов к приближенным формулам.
- Работа с библиотеками высокоточной арифметики.
Оптимальный подход к вычислению факториалов заключается в комбинировании различных методов в зависимости от размера входных данных и требуемой точности. Для небольших n (до 20-30) рекомендуется использовать прямое вычисление, для средних значений — итеративные алгоритмы с типами данных произвольной точности, а для очень больших — логарифмическое представление или приближенные формулы.
Таблица факториалов: от 1 до 20
Для удобства использования и быстрого поиска приводим расширенную таблицу значений:
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
| 11 | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
| 14 | 87 178 291 200 |
| 15 | 1 307 674 368 000 |
| 16 | 20 922 789 888 000 |
| 17 | 355 687 428 096 000 |
| 18 | 6 402 373 705 728 000 |
| 19 | 121 645 100 408 832 000 |
| 20 | 2 432 902 008 176 640 000 |
Эта таблица наглядно демонстрирует экспоненциальный рост factorial и может служить полезным справочным материалом при решении математических задач.
Заключение
Понимание factorial и умение работать с ним — это не просто математический навык, но и важный инструмент, применимый во многих областях науки и технологий. Мы рассмотрели, что факториал — это не только элегантное математическое выражение, но и мощный инструмент, необходимый для решения широкого спектра задач. Подведем итог:
- Факториал n — это произведение всех натуральных чисел от 1 до n, обозначается как n!.
- Он быстро растёт — даже при небольших значениях n результат становится огромным.
- Применяется повсеместно — в комбинаторике, теории вероятностей, математическом анализе, алгоритмах и криптографии.
- Реализуется по-разному — через рекурсию, цикл, встроенные библиотеки и приближённые формулы.
- Содержит подводные камни — переполнение памяти, рекурсивные ограничения и точность вычислений.
- Обобщается на дробные значения — с помощью гамма-функции и других продвинутых подходов.
Хотите понять не только математику, но и как применять её в реальных проектах? Посмотрите подборку курсов по PHP-разработке — там факториалы обретают практический смысл.
Рекомендуем посмотреть курсы по программированию на PHP
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Frontend-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
107 760 ₽
|
От
8 980 ₽/мес
|
Длительность
12 месяцев
|
Старт
6 февраля
|
Подробнее |
|
Frontend-разработчик
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
128 800 ₽
238 574 ₽
|
От
3 976 ₽/мес
На 2 года
|
Длительность
13 месяцев
|
Старт
5 февраля
|
Подробнее |
|
PHP-разработчик. Базовый уровень
|
Skillbox
219 отзывов
|
Цена
Ещё -20% по промокоду
80 990 ₽
161 979 ₽
|
От
6 749 ₽/мес
Без переплат на 1 год.
|
Длительность
3 месяца
|
Старт
3 февраля
|
Подробнее |
|
Профессия: ВЕБ-разработчик
|
ProductStar
41 отзыв
|
Цена
Ещё -16% по промокоду
129 600 ₽
288 000 ₽
|
От
5 520 ₽/мес
Рассрочка на 2 года.
11 600 ₽/мес
|
Длительность
10 месяцев
|
Старт
3 февраля
|
Подробнее |
|
Веб-разработчик с нуля
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
163 300 ₽
302 470 ₽
|
От
5 041 ₽/мес
Без переплат на 2 года.
7 222 ₽/мес
|
Длительность
17 месяцев
|
Старт
5 февраля
|
Подробнее |

Как сменить профессию и какую выбрать: полное руководство для тех, кто хочет начать с нуля
В этом материале подробно разбираем, как переучиться на другую профессию без хаотичных решений и лишних рисков. Вы узнаете, с чего начать, какие направления действительно востребованы и как выбрать формат обучения под свои цели.

Data Lineage: что это такое, зачем нужен и как внедрить
Что такое data lineage и почему без него сложно управлять современными потоками информации? В статье вы найдёте объяснения простыми словами, узнаете о преимуществах и получите практические советы по внедрению.

Хостинг — что это такое, как он работает и какой выбрать для сайта
Вы тоже думали, что хостинг — это нечто для программистов? На самом деле всё проще: разберёмся, зачем он нужен, какие бывают виды и как понять, какой подойдёт именно вам.

Ansible или Puppet: разбор сильных и слабых сторон
Как выбрать инструмент для управления конфигурациями? В статье мы подробно анализируем плюсы и минусы Ansible и Puppet, чтобы помочь вам сделать осознанный выбор.