Логарифмы для программистов: всё, что нужно знать
Логарифмы — тот раздел математики, который многие разработчики предпочитают обходить стороной после окончания учебных заведений. Однако эти математические инструменты играют значительную роль в оценке сложности алгоритмов, машинном обучении и эффективной обработке данных.

В этой статье мы разберемся, почему логарифмы стоит «подружить» со своим кодом, и как они могут стать неожиданным союзником в решении сложных задач программирования.
- Что такое логарифм? Понятие и основные определения
- Виды и их особенности
- Как вычислять в программировании
- Применение в программировании
- Практические задачи и упражнения
- Заключение
- Рекомендуем посмотреть курсы по программированию на PHP
Что такое логарифм? Понятие и основные определения
Для многих программистов logarithm остается абстрактной концепцией из школьного курса математики. Однако по своей сути это довольно интуитивное понятие — логарифм является обратной операцией к возведению в степень.
Представим выражение 2³ = 8. В этой формуле:
- 2 — основание степени.
- 3 — показатель степени (экспонента).
- 8 — результат возведения в степень.
Если мы захотим найти показатель степени, имея основание и результат, нам на помощь приходит logarithm. Выражение log₂ 8 = 3 означает: «3 — это степень, в которую нужно возвести 2, чтобы получить 8».
Другие примеры:
- log₁₀ 100 = 2 (потому что 10² = 100).
- log₃ 81 = 4 (потому что 3⁴ = 81).
Логарифмы позволяют нам «распаковать» экспоненциальные выражения и найти степень, необходимую для получения определенного результата. Эта, казалось бы, простая операция становится критически важным инструментом при анализе эффективности алгоритмов и работе с большими объемами данных.
Формула
Формально logarithm числа b по основанию a записывается как log_a(b) и определяется равенством:
Если a^x = b, то log_a(b) = x
Здесь:
- a — основание логарифма (положительное число, не равное 1).
- b — логарифмируемое число (положительное число).
- x — результат логарифмирования.
Примеры простых логарифмов
Давайте рассмотрим несколько примеров вычисления logarithm:
- log₁₀ 1000 = 3, потому что 10³ = 1000.
- log₂ 16 = 4, потому что 2⁴ = 16.
- log₃ 9 = 2, потому что 3² = 9.
- log₅ 125 = 3, потому что 5³ = 125.
- log₃ 1 = 0, потому что любое число в степени 0 равно 1.
- log₄ 4 = 1, потому что любое число в степени 1 равно самому себе.
Эти базовые примеры иллюстрируют ключевую идею logarithm: они позволяют нам выразить показатель степени через основание и результат возведения в степень.
История и происхождение логарифмов
Многие думают, что логарифмы — изобретение эпохи калькуляторов и программирования. Но на самом деле их история уходит корнями в начало XVII века. В 1614 году шотландский математик Джон Непер представил миру концепцию логарифмов как способ упростить сложные вычисления. В его трактате Mirifici Logarithmorum Canonis Descriptio впервые описывались свойства, позволяющие превращать умножение в сложение и деление в вычитание — за счёт логарифмов.
Спустя несколько лет швейцарский математик Йост Бюрги независимо разработал аналогичную систему. Благодаря работам Непера и Бюрги были созданы логарифмические таблицы, которые помогали учёным и инженерам до эпохи компьютеров быстро производить расчёты.
Позже Исаак Ньютон, Леонард Эйлер и другие великие математики развивали эту концепцию, связывая логарифмы с экспонентами и натуральной константой e, что легло в основу многих разделов анализа.
Сегодня, спустя 400 лет, логарифмы не утратили своей актуальности — особенно в программировании и алгоритмическом мышлении.
Виды и их особенности
В программировании и математике мы регулярно сталкиваемся с несколькими типами, каждый из которых имеет свои особенности и области применения. Выбор типа часто определяется контекстом задачи и эффективностью вычислений в конкретной ситуации.
Интересно отметить, что различные основания логарифмов появились исторически из практических потребностей разных областей науки и техники. Так, десятичные естественным образом соответствуют нашей десятичной системе счисления, в то время как двоичные идеально подходят для работы с компьютерными системами, основанными на двоичной логике.
При разработке алгоритмов выбор типа может существенно влиять на читаемость кода и его вычислительную эффективность. Например, при анализе сложности рекурсивных алгоритмов с делением задачи пополам (таких как бинарный поиск или быстрая сортировка) использование двоичного логарифма не только упрощает формулы, но и делает их более интуитивно понятными.log₂(n) — количество шагов, необходимых при бинарном поиске по массиву из n элементов
Рассмотрим основные типы, с которыми программисту приходится работать чаще всего.
Натуральный (ln)
Натуральный логарифм — это по основанию числа e (приблизительно равного 2,71828…), обозначается как ln(x). Число e — фундаментальная математическая константа, которая встречается во множестве природных процессов и связана с экспоненциальным ростом.
Натуральные широко применяются в машинном обучении, особенно в логистической регрессии и нейронных сетях. Они также являются основой для многих численных методов, включая вычисление сложных интегралов и дифференциальных уравнений. В большинстве языков программирования натуральный logarithm является «стандартным» и вычисляется по умолчанию функцией log(), если не указано иное основание.
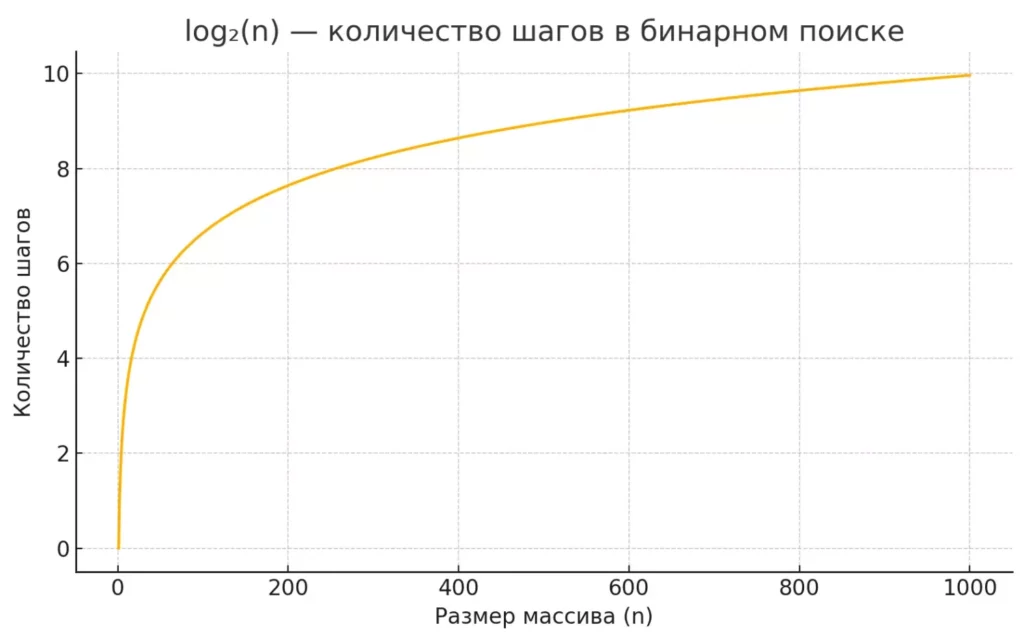
График показывает, как медленно растёт число шагов при бинарном поиске по сравнению с размером массива. Отлично визуализирует преимущество логарифмической сложности.
Десятичный (lg)
Десятичный — это логарифм по основанию 10, обозначается как lg(x) или log₁₀(x). Этот тип особенно удобен при работе с порядками величин и масштабированием данных.
В программировании десятичные часто используются для преобразования линейных шкал в логарифмические (например, при визуализации данных с большим разбросом значений). Они также полезны при работе с числами, представленными в научной нотации, и в алгоритмах, обрабатывающих числа в десятичной системе. Классический пример — вычисление количества цифр в десятичном представлении числа через формулу: floor(log₁₀(n)) + 1.
Двоичный (log2)
Двоичный — это логарифм по основанию 2, обозначается как log₂(x). Этот тип имеет особое значение в компьютерных науках, поскольку компьютеры работают с двоичной системой счисления.
Двоичные лежат в основе анализа сложности многих эффективных алгоритмов. Когда мы говорим о логарифмической сложности O(log n), речь идет именно о log₂ n. Наглядные примеры — бинарный поиск, где пространство поиска сокращается вдвое на каждой итерации, и сбалансированные деревья поиска, высота которых пропорциональна log₂ n.
Кроме того, двоичные используются при работе с битовыми операциями, в частности, для определения количества битов, необходимых для представления числа (⌊log₂ n⌋ + 1), что критично для оптимизации памяти и проектирования структур данных.
Степени и корня
Логарифмические свойства особенно полезны при работе со степенями и корнями, позволяя упростить вычисления и преобразования.
Логарифм степени: loga(xn) = n × logax
Это свойство позволяет «вынести» показатель степени в виде множителя перед logarithm. Например: log10(1002) = 2 × log10100 = 2 × 2 = 4
Логарифм корня: loga(√nx) = (1/n) × logax
Это свойство является частным случаем предыдущего, поскольку корень n-й степени можно представить как возведение в степень 1/n. Например: log10(√100) = (1/2) × log10100 = 0.5 × 2 = 1
Данные свойства особенно полезны при оценке сложности рекурсивных алгоритмов, таких как «разделяй и властвуй», где часто приходится анализировать выражения вида T(n) = aT(n/b) + f(n).
Переход к новому основанию
Одно из наиболее практичных свойств, особенно в программировании, — это возможность изменить основание:
logax = logbx / logba
Это свойство позволяет вычислять логарифмы с произвольным основанием, используя доступные в языках программирования стандартные функции. Например, чтобы вычислить log327, можно использовать натуральные logarithm:
log327 = loge27 / loge3 = ln(27) / ln(3)
Таблица свойств
| Свойство | Формула |
|---|---|
| Единицы | loga1 = 0 |
| Основания | logaa = 1 |
| Произведения | loga(x×y) = logax + logay |
| Частного | loga(x÷y) = logax — logay |
| Степени | loga(xn) = n × logax |
| Смена основания | logax = logbx / logba |
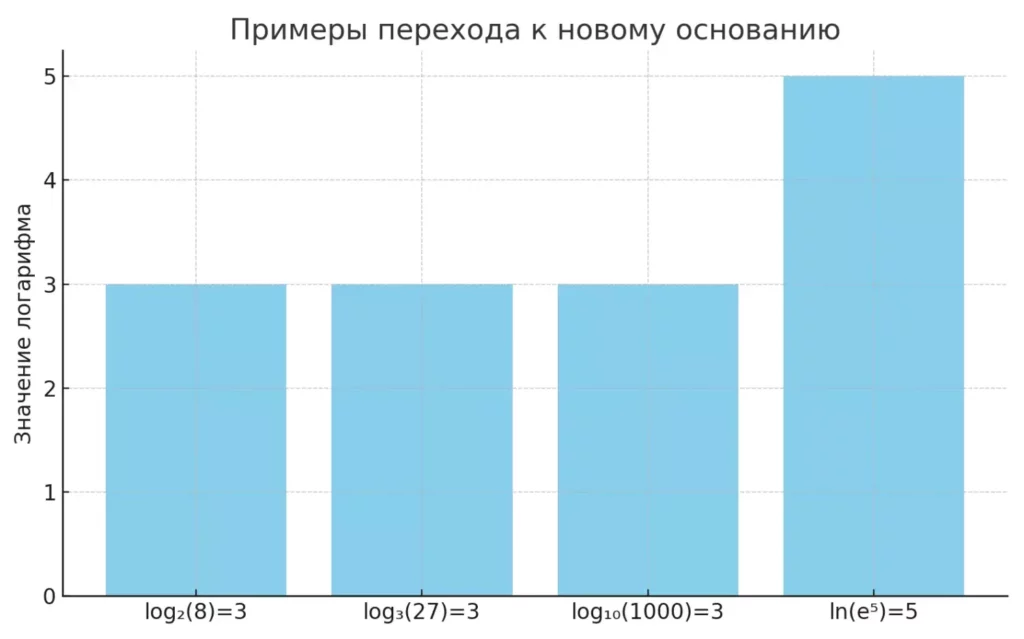
Диаграмма иллюстрирует, как одно и то же значение можно получить при помощи разных логарифмов и формулы перехода к новому основанию. Помогает лучше запомнить универсальность логарифмов в коде.
Как вычислять в программировании
В современных языках программирования расчет логарифмов — задача, которая решается с помощью встроенных математических библиотек. Тем не менее, программисту важно понимать нюансы реализации этих функций в различных языках, чтобы избежать типичных ошибок и обеспечить точность вычислений.
Интересно, что внутренняя реализация логарифмических функций в большинстве языков программирования основана на приближенных методах, таких как разложение в ряды Тейлора или итеративные алгоритмы (например, метод Ньютона). Эффективные реализации часто используют комбинацию методов для достижения оптимального баланса между скоростью и точностью.
Стоит отметить, что при работе с ними в программировании необходимо учитывать ограничения представления чисел с плавающей точкой. Ошибки округления могут накапливаться, особенно при работе с очень большими или маленькими числами, что в некоторых случаях требует использования специальных методов повышения точности или библиотек для работы с произвольной точностью.
Рассмотрим, как вычислять логарифмы в наиболее популярных языках программирования и какие особенности следует учитывать при написании кода.
В Python
Python предоставляет удобный интерфейс для работы с логарифмами через модуль math. Необходимо импортировать этот модуль перед использованием логарифмических функций:
import math
# Натуральный логарифм (основание e)
natural_log = math.log(100) # ln(100)
print(f"ln(100) = {natural_log}")
# Десятичный логарифм (основание 10)
decimal_log = math.log10(100) # log₁₀(100)
print(f"log₁₀(100) = {decimal_log}")
# Двоичный логарифм (основание 2)
binary_log = math.log2(8) # log₂(8)
print(f"log₂(8) = {binary_log}")
# Логарифм с произвольным основанием
custom_base_log = math.log(27, 3) # log₃(27)
print(f"log₃(27) = {custom_base_log}")
Обратите внимание, что функция log() может принимать второй аргумент для указания произвольного основания, что делает Python особенно удобным для работы с различными типами.
В Java
В Java вычисляются с помощью статических методов класса Math. Стандартная библиотека предоставляет методы для вычисления натурального и десятичного логарифмов, но для logarithm с произвольным основанием необходимо использовать формулу перехода:
public class LogarithmExample {
public static void main(String[] args) {
// Натуральный логарифм (основание e)
double naturalLog = Math.log(100);
System.out.println("ln(100) = " + naturalLog);
// Десятичный логарифм (основание 10)
double decimalLog = Math.log10(100);
System.out.println("log₁₀(100) = " + decimalLog);
// Логарифм с произвольным основанием
double customBaseLog = customLog(27, 3);
System.out.println("log₃(27) = " + customBaseLog);
}
// Метод для вычисления логарифма с произвольным основанием
private static double customLog(double value, double base) {
return Math.log(value) / Math.log(base);
}
}
Стоит отметить, что в новых версиях Java появился метод Math.log2() для вычисления двоичного logarithm, который особенно полезен при анализе алгоритмов и работе с битовыми операциями.
В JavaScript
В JavaScript логарифмические функции доступны через объект Math. Как и в Java, стандартная библиотека предоставляет методы для натурального, десятичного и двоичного логарифмов:
// Натуральный логарифм (основание e)
const naturalLog = Math.log(100);
console.log(`ln(100) = ${naturalLog}`);
// Десятичный логарифм (основание 10)
const decimalLog = Math.log10(100);
console.log(`log₁₀(100) = ${decimalLog}`);
// Двоичный логарифм (основание 2)
const binaryLog = Math.log2(8);
console.log(`log₂(8) = ${binaryLog}`);
// Логарифм с произвольным основанием (например, по основанию 3)
function customLog(value, base) {
return Math.log(value) / Math.log(base);
}
const customBaseLog = customLog(27, 3);
console.log(`log₃(27) = ${customBaseLog}`);
JavaScript, как и большинство интерпретируемых языков, использует 64-битное представление чисел с плавающей точкой (IEEE 754), что может приводить к небольшим погрешностям при вычислениях — факт, который следует учитывать при работе с логарифмами в критических расчетах.
Применение в программировании
Рассмотрим некоторые ключевые области применения логарифмов в современной разработке программного обеспечения.
В оценке сложности алгоритмов
Логарифмы играют фундаментальную роль в анализе алгоритмов, особенно тех, которые используют стратегию «разделяй и властвуй». Классические примеры включают:
- Бинарный поиск: алгоритм имеет сложность O(log n), поскольку на каждом шаге диапазон поиска сокращается вдвое. Для массива из миллиона элементов потребуется максимум log₂(1,000,000) ≈ 20 сравнений — впечатляющее преимущество по сравнению с линейным поиском.
- Быстрая сортировка и сортировка слиянием: имеют среднюю сложность O(n log n). Логарифмический множитель здесь происходит из-за рекурсивного деления задачи на меньшие подзадачи.
- Сбалансированные деревья поиска (например, красно-черные деревья или AVL-деревья): операции поиска, вставки и удаления имеют сложность O(log n), что делает их эффективными структурами данных для хранения упорядоченной информации.
Фундаментальное понимание логарифмической сложности позволяет разработчикам делать осознанный выбор между различными алгоритмами в зависимости от ожидаемого размера входных данных и требований к производительности.
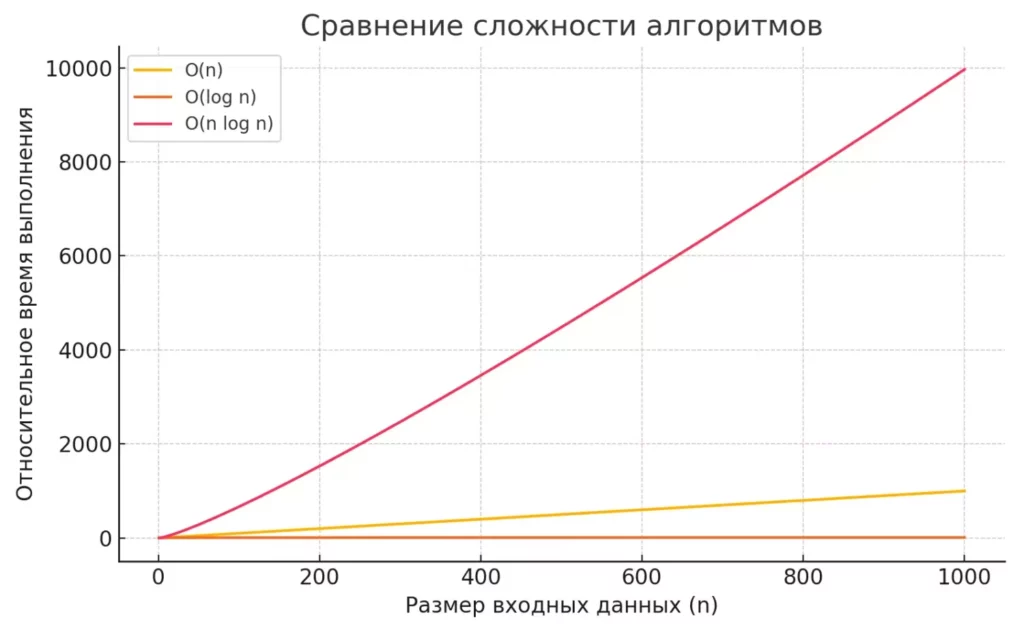
График сравнивает три типа сложности: линейную O(n), логарифмическую O(log n) и квазилинейную O(n log n). Он наглядно демонстрирует, как важна оптимизация алгоритмов в реальных задачах.
В машинном обучении
В сфере машинного обучения и анализа данных логарифмы выступают в роли важных инструментов, обеспечивающих как теоретическую основу, так и практические решения:
- Функции потерь:
Логарифмические функции широко используются в создании функций потерь, таких как кросс-энтропия в классификации. Например, в логистической регрессии минимизируется логарифмическая функция потерь, что математически эквивалентно максимизации правдоподобия:
def log_loss(y_true, y_pred): return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
- Преобразование данных:
Логарифмическая трансформация часто применяется для нормализации сильно перекошенных данных. Это особенно полезно для финансовых показателей, демографических данных или физических измерений с экспоненциальным распределением.
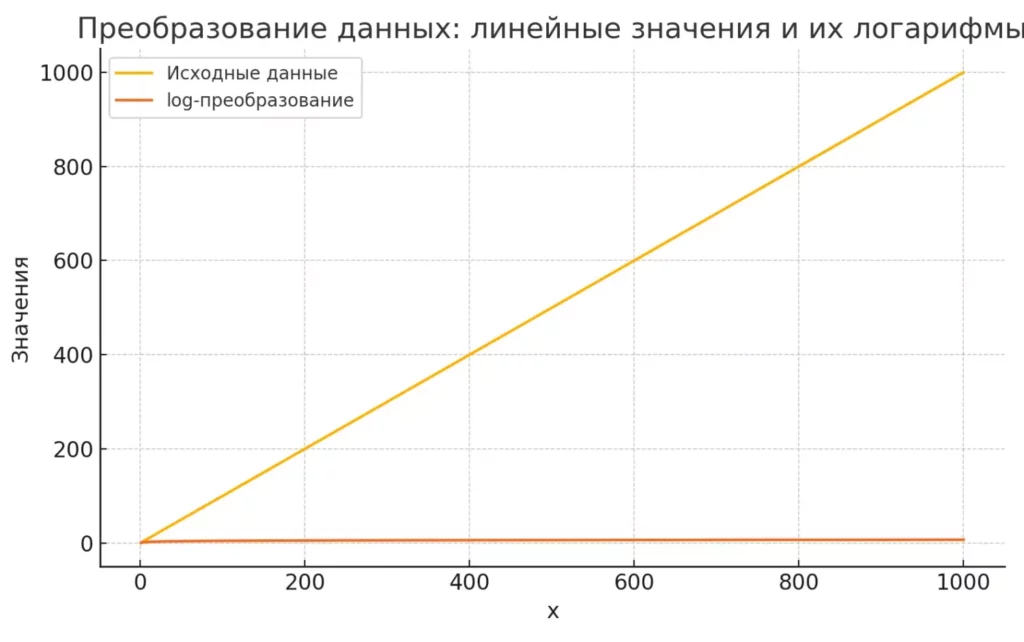
График показывает, как логарифмическое преобразование «сжимает» шкалу сильно перекошенных данных. Это важно при обработке числовых признаков в машинном обучении и статистике.
- Работа с вероятностями:
В байесовских методах часто удобнее работать с логарифмами вероятностей (log-probabilities), чтобы избежать проблем с численной устойчивостью при перемножении малых вероятностей.
Примечательно, что многие современные фреймворки машинного обучения, такие как TensorFlow и PyTorch, предлагают оптимизированные реализации логарифмических функций, специально настроенные для задач глубокого обучения и работы с градиентами.
Практические задачи и упражнения
Теория хороша, но настоящее понимание приходит через практику. Рассмотрим несколько практических задач, которые помогут закрепить знания.
Задача 1: Вычисление логарифма с произвольным основанием в Python
Реализуем функцию, которая рассчитывает logarithm с произвольным основанием и демонстрирует применение формулы перехода к новому основанию.
import math
def custom_log(value, base):
"""
Вычисляет логарифм числа value по основанию base.
Использует формулу перехода к новому основанию: log_base(value) = log(value) / log(base)
"""
if value <= 0 or base <= 0 or base == 1:
raise ValueError("Некорректные аргументы: значение и основание должны быть положительными, основание не должно равняться 1")
return math.log(value) / math.log(base)
# Проверка работы функции
print(f"log_3(27) = {custom_log(27, 3)}") # Должно вывести 3.0
print(f"log_2(8) = {custom_log(8, 2)}") # Должно вывести 3.0
Задача 2: Оптимизация алгоритма с помощью логарифмической оценки
Рассмотрим задачу нахождения целочисленной степени числа без использования встроенной операции возведения в степень. Сравним наивный линейный подход с логарифмическим алгоритмом:
# Наивный подход с линейной сложностью O(n)
def power_linear(base, exponent):
result = 1
for _ in range(exponent):
result *= base
return result
# Оптимизированный подход с логарифмической сложностью O(log n)
def power_logarithmic(base, exponent):
if exponent == 0:
return 1
# Рекурсивный случай: используем свойство x^(2n) = (x^n)^2
if exponent % 2 == 0:
half_pow = power_logarithmic(base, exponent // 2)
return half_pow * half_pow
else:
# Для нечетных степеней: x^(2n+1) = x * (x^n)^2
half_pow = power_logarithmic(base, exponent // 2)
return base * half_pow * half_pow
# Сравнение производительности на больших показателях степени
import time
base = 2
exponent = 10000
start = time.time()
power_linear(base, exponent)
linear_time = time.time() - start
start = time.time()
power_logarithmic(base, exponent)
log_time = time.time() - start
print(f"Линейный алгоритм: {linear_time:.6f} сек")
print(f"Логарифмический алгоритм: {log_time:.6f} сек")
print(f"Ускорение: {linear_time / log_time:.2f}x")
Заключение
Мы рассмотрели основные виды логарифмов, их свойства и практическое применение в программировании. Для более глубокого изучения темы рекомендуем обратиться к специализированной литературе по численным методам и алгоритмам, а также практиковаться в решении задач, требующих применения логарифмов.
- Логарифмы — это обратная операция к возведению в степень. Они помогают находить степень, к которой нужно возвести основание, чтобы получить нужное число.
- Основные типы логарифмов — натуральный, десятичный и двоичный. Каждый из них применяется в зависимости от задачи: от нейросетей до битовых операций.
- В программировании логарифмы используются для оценки сложности алгоритмов. Особенно важны в задачах «разделяй и властвуй».
- Во многих языках логарифмы реализуются через стандартные библиотеки. Но стоит учитывать особенности точности и округления.
- Логарифмы находят применение в машинном обучении. Например, в функциях потерь и логарифмической трансформации данных.
Если вы только начинаете осваивать профессию программиста, рекомендуем обратить внимание на подборку курсов по PHP-разработке. Они включают как теоретические модули, так и практические задачи — логарифмы там точно пригодятся.
Рекомендуем посмотреть курсы по программированию на PHP
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Frontend-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
95 000 ₽
|
От
7 917 ₽/мес
|
Длительность
12 месяцев
|
Старт
6 февраля
|
Ссылка на курсПодробнее |
|
PHP-разработчик. Базовый уровень
|
Академия Синергия
34 отзыва
|
Цена
55 356 ₽
138 390 ₽
|
От
2 745 ₽/мес
0% на 24 месяца
5 491 ₽/мес
|
Длительность
3 месяца
|
Старт
в любое время
|
Ссылка на курсПодробнее |
|
Frontend-разработчик
|
Нетология
45 отзывов
|
Цена
с промокодом kursy-online
122 000 ₽
225 922 ₽
|
От
3 765 ₽/мес
На 2 года
|
Длительность
13 месяцев
|
Старт
5 января
|
Ссылка на курсПодробнее |
|
PHP-разработчик. Базовый уровень
|
Skillbox
211 отзывов
|
Цена
Ещё -20% по промокоду
80 990 ₽
161 979 ₽
|
От
6 749 ₽/мес
Без переплат на 1 год.
|
Длительность
3 месяца
|
Старт
2 января
|
Ссылка на курсПодробнее |
|
Профессия: ВЕБ-разработчик
|
ProductStar
41 отзыв
|
Цена
Ещё -16% по промокоду
129 600 ₽
288 000 ₽
|
От
5 520 ₽/мес
Рассрочка на 2 года.
11 600 ₽/мес
|
Длительность
10 месяцев
|
Старт
1 января
|
Ссылка на курсПодробнее |

Живость анимации: секреты, которые оживят вашего персонажа
Как сделать так, чтобы ваш персонаж двигался как живой? Поговорим о принципах, которые превратят набор кадров в яркую и эмоциональную историю. Присоединяйтесь!

Секреты создания альпийской горки: какие камни и растения выбрать?
Альпинарий — это не просто каменная кладка, а живописная композиция, требующая грамотного подхода. Как правильно организовать горку, чтобы она выглядела естественно и гармонично?

Деловая коммуникация — что это, виды, формы и правила эффективного общения
Деловая коммуникация — это не только про официальные письма и собрания. Хотите научиться общаться ясно, уверенно и без конфликтов? Этот материал — краткий путеводитель по всему, что вам нужно знать.

Как набрать символ рубля (₽) на клавиатуре и не только
В этой статье разберём, как вводить знак рубля на разных платформах, где уместны HTML-сущности и как правильно писать суммы «1 234,56 ₽», чтобы их корректно видели все.