Рекурсия и итерация: в чём разница, как работают процессы и какой подход выбрать
В программировании существует два фундаментальных подхода к решению повторяющихся задач: рекурсия и итерация. Понимание различий между ними — важный шаг в развитии любого разработчика, поскольку выбор между этими методами напрямую влияет на производительность, читаемость кода и эффективность использования ресурсов.

Рекурсия (recursion) — это техника программирования, при которой функция вызывает саму себя для решения задачи. Каждый такой вызов работает с меньшей или более простой версией исходной проблемы, пока не будет достигнуто базовое условие — точка, в которой дальнейшие вызовы прекращаются. Можно сказать, что рекурсия разбивает сложную задачу на серию более простых подзадач, решая их последовательно через самообращение функции.
Итерация (iteration), напротив, представляет собой процесс многократного выполнения набора инструкций с использованием циклов — таких как for, while или do-while. Итеративный подход последовательно обрабатывает данные или повторяет операции до тех пор, пока заданное условие не станет ложным, при этом все вычисления происходят в рамках одного контекста выполнения.
- В чем различие
- Как работают рекурсивные и итеративные процессы
- Стек вызовов: главное, что нужно понимать о рекурсии
- Примеры реализации: рекурсия vs итерация на одной задаче
- Сравнение рекурсии и итерации: таблица отличий
- Преимущества и недостатки рекурсии
- Преимущества и недостатки итерации
- Хвостовая рекурсия: как она может стать итерацией
- Когда использовать рекурсию, а когда — итерацию
- Заключение
- Рекомендуем посмотреть курсы по Java
В чем различие
Ключевое различие между этими подходами можно сформулировать так: recursion основана на принципе «функция вызывает саму себя», тогда как итерация полагается на «повторение через циклы». В рекурсии мы делегируем решение подзадач новым вызовам той же функции, а в итерации явно управляем процессом повторения с помощью управляющих конструкций языка.
Давайте рассмотрим простую аналогию из реальной жизни. Представьте, что вам нужно найти нужную книгу в стопке.
Итеративный подход: вы берете книги одну за другой, проверяете каждую, пока не найдете нужную.
Рекурсивный подход: вы просите помощника проверить верхнюю книгу, и если это не та, он передает оставшуюся стопку следующему помощнику с той же инструкцией — и так далее, пока кто-то не найдет искомую книгу и не передаст результат обратно по цепочке.

Итерация предполагает последовательную обработку элементов — шаг за шагом в одном контексте. Рекурсия делегирует задачу дальше, создавая цепочку вложенных вызовов, которые возвращают результат обратно.
Иллюстрация наглядно показывает различие логики работы этих подходов.
На концептуальном уровне основные отличия сводятся к следующему:
- Рекурсия создает новый контекст выполнения при каждом вызове; итерация работает в одном контексте.
- Рекурсия требует базового условия для остановки; итерация — условия завершения цикла.
- Рекурсия использует стек вызовов для хранения состояния; итерация хранит состояние в переменных.
- Рекурсия естественна для задач с древовидной или вложенной структурой; итерация — для последовательных операций.
Возникает вопрос: если оба подхода решают похожие задачи, почему в языках программирования существуют оба механизма? Ответ кроется в том, что для разных типов задач один подход может оказаться значительно удобнее и эффективнее другого.
Как работают рекурсивные и итеративные процессы
Чтобы глубже понять различия между рекурсией и итерацией, необходимо рассмотреть, как именно эти процессы выполняются на уровне вычислений. Речь идет не просто о синтаксических различиях в коде, а о фундаментально разных способах организации вычислительного процесса.
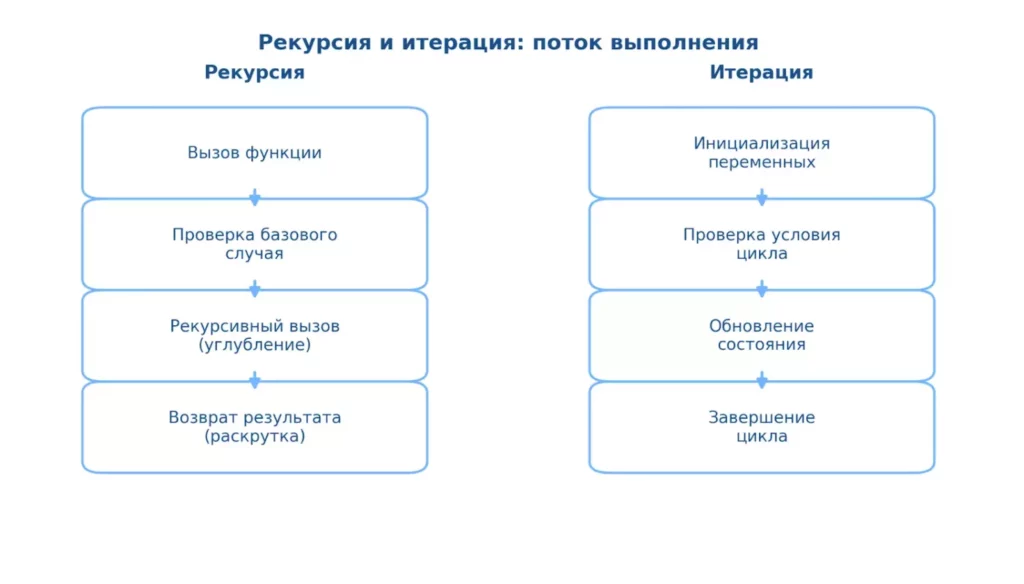
Диаграмма показывает, как отличается поток выполнения при рекурсии и итерации.
В рекурсии управление уходит вглубь через повторные вызовы функции и возвращается только после достижения базового случая.
В итерации все операции выполняются последовательно в одном контексте с обновлением состояния на каждом шаге.
Рекурсивный процесс
Рекурсивный процесс характеризуется тем, что вычисления откладываются до момента достижения базового случая. Когда функция вызывает саму себя, она не завершает свою работу немедленно — вместо этого она ожидает результата от вложенного вызова, чтобы продолжить собственные вычисления.
Этот механизм работает по принципу «сначала углубление — потом раскрутка». Функция погружается все глубже в цепочку вызовов, создавая последовательность отложенных операций. Каждый новый вызов добавляет слой в стек вызовов, сохраняя информацию о том, какие действия нужно выполнить после получения результата. Только достигнув базового условия, процесс начинает «раскручиваться» обратно: самый глубокий вызов возвращает результат предыдущему, тот обрабатывает его и передает еще выше — и так до самого первого вызова.
Накопление и хранение состояния — критический аспект рекурсивных процессов. Каждый активный вызов функции сохраняет свои локальные переменные, параметры и точку возврата в стеке. Это означает, что система должна «помнить» всю цепочку вызовов одновременно. Представьте матрешку: чтобы добраться до самой маленькой, нужно открыть все внешние — и все они остаются открытыми до тех пор, пока вы не начнете собирать их обратно.
Именно поэтому рекурсивные процессы требуют дополнительной памяти, пропорциональной глубине recursion. Если функция вызывает себя тысячу раз, в памяти одновременно существует тысяча контекстов выполнения, ожидающих своей очереди на обработку результата.
Итеративный процесс
Итеративный процесс работает принципиально иначе: вычисления выполняются немедленно, без отложенных операций. На каждом шаге цикла все необходимые операции завершаются полностью, и результат сразу же обновляет состояние программы.
В отличие от рекурсии, итерация не нуждается в накоплении «истории» вычислений. Вся информация, необходимая для продолжения работы, хранится в нескольких переменных, которые последовательно обновляются на каждой итерации цикла. Это можно сравнить с калькулятором: вы вводите число, выполняете операцию, получаете результат — и этот результат становится входными данными для следующей операции. Промежуточные состояния не сохраняются, не требуют дополнительной памяти.
Последовательное обновление переменных — ключевая характеристика итеративного подхода. Например, при вычислении факториала в цикле мы просто умножаем накопленный результат на текущее число, обновляем переменную-счетчик и переходим к следующей итерации. Все происходит «на месте», без создания новых контекстов выполнения.
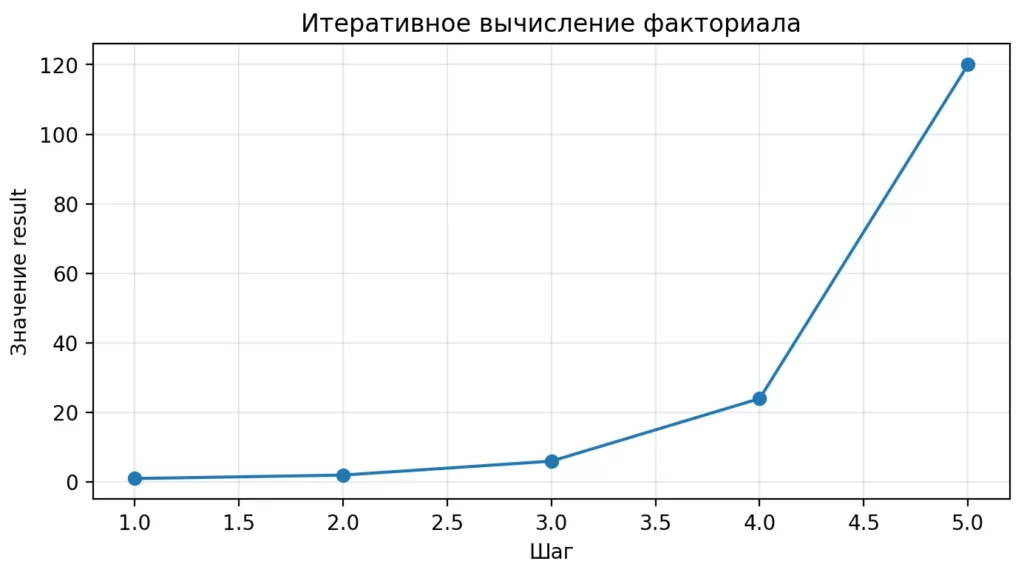
График показывает, как результат вычисления факториала обновляется на каждом шаге цикла. Все вычисления происходят сразу, без накопления отложенных операций. Используется один и тот же контекст выполнения.
Можно провести такую аналогию: рекурсия похожа на составление списка дел, где каждая задача порождает новый список подзадач, и вы не можете закрыть родительскую задачу, пока не выполнены все дочерние. Итерация же напоминает конвейер: каждый элемент обрабатывается полностью, результат фиксируется, и вы сразу переходите к следующему элементу, не оглядываясь назад.
Важно понимать, что выбор между процессамине всегда очевиден из синтаксиса кода. Некоторые языки программирования оптимизируют определенные виды рекурсии (например, хвостовую), превращая рекурсивный код в итеративный процесс на уровне выполнения. Но об этом мы поговорим подробнее в одном из следующих разделов.
Стек вызовов: главное, что нужно понимать о рекурсии
Чтобы по-настоящему понять, почему рекурсия работает именно так, а не иначе, и почему она потребляет больше ресурсов, чем итерация, необходимо разобраться с концепцией стека вызовов — одной из фундаментальных структур данных в работе программ.
Стек вызовов (call stack) — это специальная область памяти, которая используется программой для отслеживания активных вызовов функций. Каждый раз, когда вызывается функция, в стек добавляется новый элемент — так называемый стек-фрейм (stack frame), который содержит информацию о параметрах функции, локальных переменных и адрес возврата (то есть точку в коде, куда нужно вернуться после завершения функции).
Когда мы используем рекурсию, каждый новый вызов функции создает свой собственный стек-фрейм и помещает его на вершину стека. Представьте стопку тарелок: каждая новая тарелка кладется сверху, и снять можно только верхнюю. Точно так же работает стек — структура данных типа LIFO (Last In, First Out): последний добавленный элемент извлекается первым.
Допустим, функция factorial(5) вызывает factorial(4), та вызывает factorial(3) и так далее. В какой-то момент в стеке вызовов одновременно находятся фреймы для factorial(5), factorial(4), factorial(3), factorial(2) и factorial(1). Каждый из этих фреймов занимает память и ожидает, когда следующий уровень вернет результат. Только после того как factorial(1) вернет значение, начинает освобождаться стек: сначала завершается factorial(2), затем factorial(3) — и так далее, пока мы не вернемся к исходному вызову.
Именно поэтому рекурсивные процессы потребляют больше памяти по сравнению с итеративными. Глубина рекурсии напрямую определяет количество стек-фреймов, существующих одновременно. Если функция вызывает себя тысячу раз, в памяти создается тысяча фреймов — и все они должны храниться до завершения самого глубокого вызова.
Размер стека вызовов ограничен операционной системой и виртуальной машиной языка программирования. Когда глубина рекурсии превышает допустимый лимит, возникает ошибка stack overflow (переполнение стека). Это одна из наиболее распространенных проблем при работе с рекурсией: даже логически корректная рекурсивная функция может привести к аварийному завершению программы, если количество вложенных вызовов окажется слишком большим.
Итеративные решения, напротив, используют один и тот же стек-фрейм на протяжении всего выполнения цикла. Независимо от того, сколько итераций выполняет цикл — десять или миллион, — размер стека остается постоянным. Все промежуточные данные хранятся в обычных переменных, а не в стеке вызовов, что делает итерацию значительно более безопасной с точки зрения использования памяти.
Понимание работы стека вызовов критически важно при выборе между рекурсией и итерацией, особенно когда речь идет о задачах с потенциально большой глубиной вложенности.
Примеры реализации: рекурсия vs итерация на одной задаче
Теория становится по-настоящему понятной только при рассмотрении конкретных примеров. Давайте разберем классическую задачу вычисления факториала — она достаточно проста для понимания, но при этом отлично демонстрирует различия между рекурсивным и итеративным подходами.
Рекурсивное решение задачи
Факториал числа n (обозначается как n!) — это произведение всех натуральных чисел от 1 до n. Например, 5! = 5 × 4 × 3 × 2 × 1 = 120. Рекурсивное определение факториала выглядит элегантно: n! = n × (n-1)!, при этом 0! = 1 (базовый случай).
Вот как это выглядит в коде на Python:
def factorial_recursive(n): # Базовый случай: факториал 0 равен 1 if n == 0: return 1 # Рекурсивный случай: n! = n × (n-1)! return n * factorial_recursive(n - 1) result = factorial_recursive(5) print(result) # Вывод: 120
В этой реализации функция вызывает саму себя с уменьшенным аргументом. При вызове factorial_recursive(5) происходит следующая цепочка вызовов:
- factorial_recursive(5) вызывает factorial_recursive(4).
- factorial_recursive(4) вызывает factorial_recursive(3).
- factorial_recursive(3) вызывает factorial_recursive(2).
- factorial_recursive(2) вызывает factorial_recursive(1).
- factorial_recursive(1) вызывает factorial_recursive(0).
- factorial_recursive(0) возвращает 1 (базовый случай).
Затем начинается «раскрутка»: каждый вызов умножает полученный результат на свое значение n и возвращает его вызвавшей функции.
Итеративное решение той же задачи
Теперь посмотрим на итеративную реализацию той же задачи:
def factorial_iterative(n): result = 1 # Последовательно умножаем result на каждое число от 2 до n for i in range(2, n + 1): result *= i return result result = factorial_iterative(5) print(result) # Вывод: 120
Здесь мы используем цикл for, который перебирает числа от 2 до n включительно, последовательно накапливая произведение в переменной result. Никаких дополнительных вызовов функций не происходит — все вычисления выполняются в рамках одного контекста.
Что происходит «под капотом» в каждом случае
Различия между этими подходами становятся особенно наглядными, если проанализировать, что происходит в памяти и как выполняются вычисления.
В рекурсивном случае создается пять стек-фреймов (для n от 5 до 1), каждый из которых хранит свое значение параметра n и ожидает результата от следующего вызова. Вычисления откладываются: умножение на 5 не может произойти, пока не получен результат от factorial_recursive(4), а тот, в свою очередь, ждет результата от factorial_recursive(3) — и так далее. Только достигнув базового случая (n = 0), система начинает выполнять отложенные умножения в обратном порядке: 1 × 1 = 1, затем 1 × 2 = 2, затем 2 × 3 = 6, затем 6 × 4 = 24, и наконец 24 × 5 = 120.
В итеративном случае используется только один стек-фрейм для функции factorial_iterative. Переменная result последовательно обновляется на каждой итерации цикла: сначала 1 × 2 = 2, затем 2 × 3 = 6, затем 6 × 4 = 24, затем 24 × 5 = 120. Вычисления выполняются немедленно, без откладывания операций, и промежуточные результаты не требуют хранения множественных контекстов выполнения.
Можно сказать, что рекурсия работает как стопка заметок, где каждая следующая записка кладется поверх предыдущей, и разбирать их можно только в обратном порядке. Итерация же напоминает блокнот, где мы просто последовательно перезаписываем результат на одной и той же странице.
Сравнение рекурсии и итерации: таблица отличий
Для систематизации всей информации, которую мы рассмотрели выше, представим основные различия между рекурсией и итерацией в виде сводной таблицы. Это позволит наглядно увидеть, в каких аспектах один подход превосходит другой, а где они оказываются примерно равнозначными.
| Критерий | Рекурсия | Итерация |
|---|---|---|
| Определение | Функция вызывает саму себя для решения задачи | Набор инструкций выполняется многократно в цикле |
| Условие завершения | Базовый случай (base case), при котором прекращаются дальнейшие вызовы | Условие продолжения цикла становится ложным |
| Использование памяти | Высокое — каждый вызов создает новый стек-фрейм | Низкое — используется один стек-фрейм независимо от количества итераций |
| Временная сложность | Часто выше или равна итерации; может значительно возрасти без оптимизации (например, динамического программирования) | Обычно ниже или равна рекурсии |
| Риск переполнения стека | Высокий при глубокой рекурсии (stack overflow) | Отсутствует — стек не растет |
| Читаемость кода | Часто проще и элегантнее для задач с естественной рекурсивной структурой (деревья, графы) | Может быть более многословной, но понятнее для простых повторяющихся операций |
| Накладные расходы | Есть — связаны с созданием и управлением множественными вызовами функций | Минимальные — нет вызовов функций, только управление циклом |
| Производительность | Ниже из-за накладных расходов на вызовы функций и использование стека | Выше — более эффективное использование ресурсов |
| Подходящие задачи | Обход деревьев и графов, задачи типа «разделяй и властвуй» (merge sort, quick sort), задачи с естественной рекурсивной структурой (Ханойские башни, генерация комбинаций) | Простые циклические операции, обработка массивов, задачи с высокими требованиями к производительности, большие объемы данных |
Важно понимать, что эта таблица отражает общие тенденции, но не абсолютные правила. Существуют ситуации, когда рекурсивное решение может быть оптимизировано до уровня итеративного (например, через хвостовую рекурсию), или когда итеративный код становится настолько сложным, что теряет преимущество в читаемости.
Преимущества и недостатки рекурсии
Давайте разберем, когда она становится преимуществом, а когда превращается в источник проблем.
Преимущества:
- Естественность для определенных задач. Некоторые задачи имеют внутреннюю рекурсивную структуру, и решение напрямую отражает математическое или логическое определение проблемы. Например, обход дерева или вычисление чисел Фибоначчи естественно описываются через рекурсию.
- Краткость и элегантность кода. Рекурсивные решения часто требуют значительно меньше строк кода по сравнению с итеративными аналогами. Функция для обхода бинарного дерева может занять 5-7 строк в этом варианте, тогда как итеративная реализация с явным стеком потребует 20-30 строк.
- Упрощение сложной логики. Рекурсия позволяет разбить сложную задачу на более простые подзадачи идентичной природы. Это облегчает понимание алгоритма и его реализацию, особенно в задачах типа «разделяй и властвуй».
- Удобство при работе с древовидными структурами. Деревья, графы, вложенные структуры данных — все это естественно обрабатывается рекурсией, поскольку сама их природа рекурсивна (узел дерева содержит поддеревья, которые тоже являются деревьями).
Недостатки:
- Высокие накладные расходы. Каждый вызов функции требует создания нового стек-фрейма, сохранения контекста, передачи параметров и последующего восстановления состояния. Это создает существенные накладные расходы по сравнению с простым циклом.
- Риск переполнения стека. Stack overflow — реальная угроза при глубокой рекурсии. Даже корректный алгоритм может привести к аварийному завершению программы, если глубина превысит лимит стека (обычно несколько тысяч вызовов).
- Повышенное потребление памяти. Рекурсивные процессы требуют памяти пропорционально глубине. Для задачи с глубиной рекурсии 10 000 может потребоваться несколько мегабайт только на стек вызовов.
- Сложность отладки. Отслеживание состояния программы через множество уровней вызовов может быть затруднительным. Стек-трейс при ошибке содержит десятки одинаковых вызовов, что усложняет поиск источника проблемы.
- Потенциальная неэффективность без оптимизации. Некоторые наивные рекурсивные решения (например, вычисление чисел Фибоначчи) выполняют одни и те же вычисления многократно, что приводит к экспоненциальной временной сложности. Без применения мемоизации или динамического программирования такие решения непригодны для практического использования.
- Зависимость от оптимизаций компилятора. Эффективность может сильно зависеть от того, поддерживает ли язык программирования оптимизацию хвостовой рекурсии. В языках без такой оптимизации даже хвостово-рекурсивный код будет потреблять линейную память.
Преимущества и недостатки итерации
Итерация традиционно считается более «практичным» и «промышленным» подходом к решению повторяющихся задач. Давайте разберем, что делает итерацию предпочтительным выбором в большинстве production-сценариев, и в каких случаях она может уступать рекурсии.
Преимущества итерации:
- Высокая производительность. Итеративные решения не создают накладных расходов на вызовы функций, что делает их значительно быстрее рекурсивных аналогов. Цикл просто обновляет переменные и переходит к следующей итерации — никаких затрат на управление стеком.
- Эффективное использование памяти. Независимо от количества итераций, используется один и тот же стек-фрейм. Это позволяет обрабатывать миллионы элементов без риска переполнения памяти.
- Отсутствие риска stack overflow. Итеративный код не может вызвать переполнение стека, что делает его более надежным и предсказуемым в поведении, особенно при работе с большими объемами данных.
- Простота отладки. Состояние программы в любой момент времени определяется значениями нескольких переменных, которые легко отслеживать в отладчике. Нет необходимости анализировать глубокие стеки вызовов.
- Предсказуемость поведения. Итеративный код ведет себя одинаково на всех платформах и во всех языках программирования. Нет зависимости от наличия или отсутствия оптимизаций компилятора.
- Понятность для простых задач. Когда речь идет о последовательной обработке элементов массива или выполнении повторяющихся операций, циклы for или while интуитивно понятны даже начинающим разработчикам.
Недостатки итерации:
- Многословность для сложных структур. Когда задача естественно рекурсивна (например, обход дерева), итеративное решение требует явного управления стеком или очередью. Это значительно увеличивает объем кода и усложняет его понимание.
- Менее естественное выражение алгоритма. Для задач типа «разделяй и властвуй» итеративная реализация может выглядеть искусственно и менее интуитивно по сравнению с рекурсивной, которая напрямую отражает математическое определение.
- Потенциальная сложность логики. В некоторых случаях итеративный код становится трудночитаемым из-за необходимости явно отслеживать состояние, которое в recursion управляется автоматически через параметры функции.
- Ограниченность при работе с вложенными структурами. Обход многоуровневых вложенных структур (например, файловой системы произвольной глубины) итеративно требует дополнительных структур данных для хранения промежуточных состояний.
В целом, итерация представляет собой более «земной» и практичный подход. Она предпочтительна в тех случаях, когда важны производительность, надежность и эффективное использование ресурсов. Согласно нашим наблюдениям, в современной разработке итеративные решения составляют подавляющее большинство production-кода именно потому, что они обеспечивают предсказуемое и стабильное поведение программ при работе с реальными объемами данных.
Однако это не означает, что итерация всегда лучше — просто у нее другая область применения. Там, где рекурсия естественна и глубина вложенности ограничена, отказ от нее в пользу итерации может привести к неоправданному усложнению кода.
Хвостовая рекурсия: как она может стать итерацией
Существует особая форма, которая позволяет обойти главный недостаток рекурсивных решений — избыточное потребление памяти стека. Речь идет о хвостовой рекурсии (tail recursion) — технике, при которой вызов является последней операцией в функции.
Это рекурсия, в которой вызов функции самой себя происходит в самом конце, и результат этого вызова сразу возвращается без каких-либо дополнительных вычислений. Ключевое отличие от обычной: после рекурсивного вызова не выполняется никаких операций — нет умножений, сложений или других действий с возвращенным значением.
Рассмотрим пример. Обычная рекурсия для факториала выглядит так:
def factorial(n): if n == 0: return 1 return n * factorial(n - 1) # умножение ПОСЛЕ вызова
Здесь умножение на n происходит после возврата из рекурсивного вызова, поэтому это не хвостовая. А вот хвостово-рекурсивная версия:
def factorial_tail(n, accumulator=1): if n == 0: return accumulator return factorial_tail(n - 1, n * accumulator) # вызов в хвосте
В этой версии все вычисления (умножение) выполняются до рекурсивного вызова и передаются через параметр-аккумулятор. Этот вызов — это последнее, что делает функция.
Как работает tail call optimization (TCO)? Компиляторы и интерпретаторы, поддерживающие оптимизацию хвостовых вызовов, распознают такую структуру кода и преобразуют рекурсию в итерацию на уровне машинного кода. Вместо создания нового стек-фрейма система просто обновляет параметры функции и переходит к началу — точно так же, как работает цикл. Таким образом, хвостовая не приводит к росту стека, независимо от глубины рекурсии.
Это означает, что хвостово-рекурсивная функция может вызвать себя миллион раз, но при этом использовать постоянное количество памяти — как обычный итеративный цикл. Stack overflow становится невозможен.
Поддержка в языках программирования. К сожалению, не все языки поддерживают оптимизацию хвостовой рекурсии. Например:
- JavaScript (в стандарте ES6 TCO предусмотрена, но большинство движков ее не реализуют).
- Scala, Scheme, Erlang, Elixir — полная поддержка и гарантированная оптимизация.
- Python — TCO не поддерживается по философским соображениям (Гвидо ван Россум считает, что это затрудняет отладку).
- C, C++ — зависит от уровня оптимизации компилятора.
- Java — не поддерживается на уровне JVM.
Можно сказать, что хвостовая — это элегантный способ получить выразительность рекурсивного кода с производительностью итерации. Однако возможность использования этого подхода целиком зависит от выбранного языка программирования и настроек компилятора, что ограничивает его применимость в реальных проектах.
Когда использовать рекурсию, а когда — итерацию
Выбор между рекурсией и итерацией — это не вопрос личных предпочтений, а осознанное решение, основанное на природе задачи, требованиях к производительности и характеристиках используемого языка программирования. Давайте систематизируем ситуации, в которых один подход оказывается предпочтительнее другого.
Когда лучше рекурсия
- Древовидные и графовые структуры. Деревья и графы по своей природе рекурсивны: каждый узел может содержать поддеревья или связи с другими узлами. Обход таких структур — естественное решение. Примеры: обход файловой системы, парсинг DOM-дерева, поиск в бинарном дереве поиска.
- Обходы в глубину (DFS). Алгоритмы поиска в глубину традиционно реализуются рекурсивно, поскольку логика «углубиться, затем вернуться и попробовать другой путь» естественно выражается через рекурсивные вызовы.
- Алгоритмы «разделяй и властвуй». Задачи, которые можно разбить на несколько независимых подзадач меньшего размера, идеально подходят для рекурсии. Классические примеры: сортировка слиянием (merge sort), быстрая сортировка (quick sort), бинарный поиск.
- Задачи с естественным математическим рекурсивным определением. Когда математическое или логическое определение задачи само по себе рекурсивно (числа Фибоначчи, вычисление степени, генерация всех подмножеств множества), рекурсивная реализация напрямую отражает это определение.
- Обратный ход (backtracking). Алгоритмы с откатом назад при неудачной попытке — например, решение судоку, задача о N ферзях, генерация всех перестановок — естественно выражаются через рекурсию.
- Сложные вложенные структуры неизвестной глубины. Когда заранее неизвестно, сколько уровней вложенности имеет структура данных (например, JSON произвольной глубины), рекурсия позволяет элегантно обработать любое количество уровней.
Когда лучше итерация
- Большие объемы данных с предсказуемой структурой. Когда нужно обработать массив из миллионов элементов или выполнить операцию заданное количество раз, итерация — безопасный и эффективный выбор. Примеры: обработка лог-файлов, анализ больших датасетов, массовые вычисления.
- Простые повторяющиеся операции. Задачи типа «выполнить действие N раз» или «пройти по всем элементам последовательно» не имеют рекурсивной природы и естественно решаются циклами.
- Высокие требования к производительности. В критичных к производительности участках кода (hot paths) итерация предпочтительна из-за отсутствия накладных расходов на вызовы функций и использование стека.
- Ограниченные ресурсы памяти. В embedded-системах, мобильных приложениях или микросервисах с жесткими лимитами памяти итерация обеспечивает предсказуемое и минимальное потребление ресурсов.
- Задачи с линейной логикой выполнения. Когда алгоритм представляет собой последовательность шагов без ветвлений и вложенности, итерация делает код более читаемым и понятным.
- Отсутствие поддержки TCO в языке. Если используемый язык программирования не оптимизирует хвостовую рекурсию (например, Python), даже хвостово-рекурсивный код рискует вызвать stack overflow, и итерация становится единственным безопасным выбором.
Возникает вопрос: что делать, когда задача естественно рекурсивна, но требует обработки больших объемов данных? В таких случаях можно использовать гибридный подход: явно управляемый стек или очередь в итеративном коде. Это позволяет сохранить логику рекурсивного алгоритма, но избежать ограничений стека вызовов.
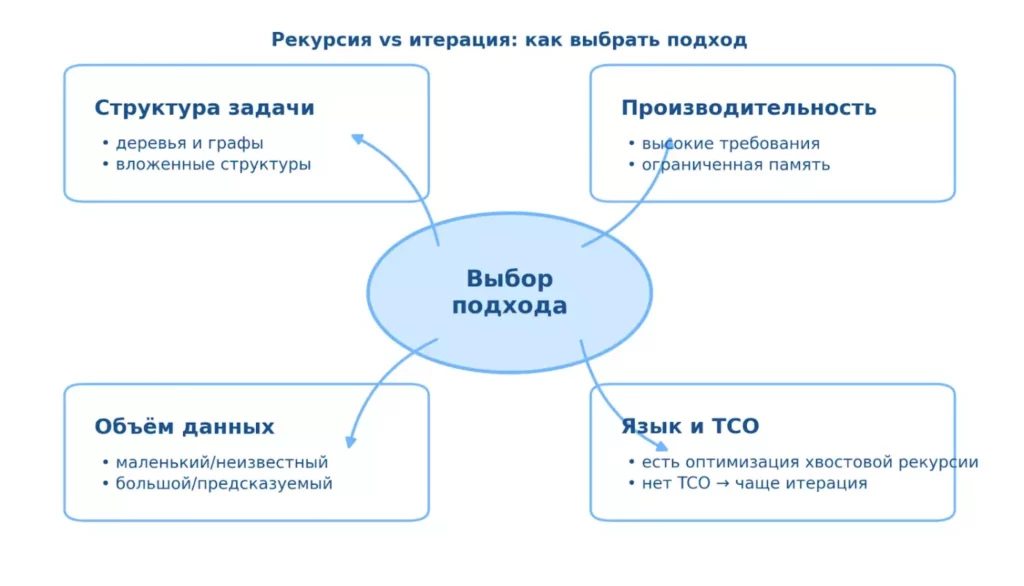
Эта майнд-карта помогает быстро выбрать между рекурсией и итерацией по четырём критериям: структура задачи, объём данных, требования к производительности и особенности языка (TCO). Используй её как чек-лист перед реализацией алгоритма. Особенно полезна, когда решение «на грани» и нужно учесть ограничения памяти/стека.
Заключение
Мы рассмотрели рекурсию и итерацию с разных сторон — от теоретических основ до практических примеров применения. Давайте сформулируем ключевые выводы, которые помогут принимать обоснованные решения при выборе подхода к решению конкретных задач:
- Итерация и рекурсия решают похожие задачи. Отличие заключается в способе организации вычислений и управлении состоянием.
- Рекурсия использует стек вызовов. Это делает код выразительным, но увеличивает потребление памяти.
- Итерация работает в одном контексте выполнения. Такой подход обычно быстрее и безопаснее при больших объемах данных.
- Хвостовая рекурсия частично снимает ограничения. Однако ее эффективность зависит от поддержки оптимизации в языке.
- Выбор подхода всегда зависит от структуры задачи. Универсального решения, подходящего для всех случаев, не существует.
Если вы только начинаете осваивать профессию программиста, рекомендуем обратить внимание на подборку курсов по Java-разработке. В них сочетается теоретическая база и практическая работа с алгоритмами, включая итерацию и рекурсию, что помогает быстрее закрепить материал.
Рекомендуем посмотреть курсы по Java
| Курс | Школа | Цена | Рассрочка | Длительность | Дата начала | Ссылка на курс |
|---|---|---|---|---|---|---|
|
Java-разработчик
|
Eduson Academy
100 отзывов
|
Цена
Ещё -5% по промокоду
115 000 ₽
|
От
9 583 ₽/мес
0% на 24 месяца
15 476 ₽/мес
|
Длительность
8 месяцев
|
Старт
скоро
Пн,Ср, 19:00-22:00
|
Подробнее |
|
Профессия Java-разработчик
|
Skillbox
219 отзывов
|
Цена
Ещё -20% по промокоду
190 971 ₽
381 943 ₽
|
От
5 617 ₽/мес
Это минимальный ежемесячный платеж. От Skillbox без %.
8 692 ₽/мес
|
Длительность
9 месяцев
Эта длительность обучения очень примерная, т.к. все занятия в записи (но преподаватели ежедневно проверяют ДЗ). Так что можно заниматься более интенсивно и быстрее пройти курс или наоборот.
|
Старт
7 февраля
|
Подробнее |
|
Java-разработчик с нуля
|
Нетология
46 отзывов
|
Цена
с промокодом kursy-online
143 700 ₽
266 020 ₽
|
От
4 433 ₽/мес
Без переплат на 2 года.
|
Длительность
14 месяцев
|
Старт
16 февраля
|
Подробнее |
|
Java-разработчик
|
Академия Синергия
35 отзывов
|
Цена
Ещё -5% по промокоду
103 236 ₽
|
От
4 302 ₽/мес
0% на 24 месяца
|
Длительность
6 месяцев
|
Старт
17 февраля
|
Подробнее |
|
Java-разработка
|
Moscow Digital Academy
66 отзывов
|
Цена
132 720 ₽
165 792 ₽
|
От
5 530 ₽/мес
на 12 месяца.
6 908 ₽/мес
|
Длительность
12 месяцев
|
Старт
в любое время
|
Подробнее |

Гибридное управление проектами: что это, как работает и когда помогает бизнесу
Гибридное управление проектами всё чаще используют там, где чистый Agile или Waterfall не дают нужного результата. Как понять, подойдёт ли этот подход именно вашему проекту, какие методологии можно сочетать и на что обратить внимание при внедрении?

Методы сортировки: полный разбор и сравнение алгоритмов от пузырьковой до быстрой
Алгоритмы сортировки используются почти в каждом приложении, но как выбрать подходящий вариант под конкретную задачу? Разберёмся, чем отличаются популярные методы, где они применяются и на что стоит обращать внимание разработчику.

Почему Selenium и Java — лучший дуэт для автоматизации тестирования?
Автоматизация тестирования требует надежных инструментов. Узнайте, как Selenium с Java помогает создавать эффективные автотесты и какие ошибки стоит избегать.

Микросервисы на Java: Почему крупные компании выбирают этот подход?
Узнайте, как микросервисы на Java помогут вашему бизнесу справиться с нагрузками и стать гибче, с примерами и советами.